Ungleichheitsrechner
Anweisungen: Verwenden Sie den Ungleichungsrechner, um eine beliebige Ungleichung zu lösen, die Sie zur Verfügung stellen, und zeigen Sie alle Schritte an. Bitte geben Sie die Ungleichung, die Sie lösen möchten, in das unten stehende Feld ein:
Mehr über das lösen von ungleichungen
Mit diesem Rechner können Sie Ungleichungen lösen, die Sie selbst eingeben. Alles, was Sie tun müssen, ist, die gewünschte Ungleichung in das Feld einzugeben und sicherzustellen, dass Sie eine gültige Ungleichung angeben.
Sie könnten zum Beispiel etwas wie "2x^2 - x >= 1/2" oder etwas wie "sin(x) > 0" angeben, solange Sie gültige Werte angeben. Achten Sie auch darauf, dass Sie ein Ungleichheitszeichen wie ">", "<", ">=" oder "<=" verwenden.
Wenn Sie stattdessen "=" verwenden, fungiert dieser Rechner als gleichungsrechner .
Sobald Sie eine gültige Ungleichung eingegeben haben, klicken Sie auf "Lösen", und im Bruchteil einer Sekunde wird Ihnen die Lösung Schritt für Schritt angezeigt. Eine Einschränkung: Nicht alle Ungleichungen können gelöst werden, denken Sie also daran.
Nicht alle Ungleichungen sind einfach zu lösen, und wir können auch nicht alle vorgefassten Methoden anwenden. Nur einige Arten, wie zum Beispiel lineare Ungleichungen , quadratische Ungleichungen oder polynomielle Gleichungen (für niedrigere Abschlüsse) lassen eine systematische Behandlung zu.

Was ist eine ungleichheit?
Eine Ungleichung ist eine Art von mathematischem Objekt, das einer mathematische Gleichung mit dem Unterschied, dass eine Ungleichung anstelle von "=" entweder ">", "<", ">=" oder "<=" enthält. Dieser kleine Unterschied im Aussehen macht das Lösen einer Ungleichung noch komplexer als das einer Gleichung.
Der folgende Ausdruck ist zum Beispiel eine Ungleichung
\[\displaystyle x + \frac{1}{3} < x^2 \]Es handelt sich also um einen mathematischen Ausdruck, der zwei Seiten hat, die linke und die rechte Seite, und das entsprechende Ungleichheitszeichen ist "<". Die obige Ungleichung ist eine quadratische Ungleichung, weil die Ausdrücke auf der linken und rechten Seite beide polynomisch sind und der höchste Grad 2 ist.
Die nachstehende Ungleichung ist zum Beispiel eine trigonometrische Ungleichung:
\[\displaystyle x + \frac{1}{3} \le \sin\left(x^2 + \frac{1}{x}\right) \]Es ist eine Ungleichung, weil sie das Ungleichheitszeichen \(\le\) hat und die rechte Seite ein trigonometrischer Ausdruck . Beachten Sie, dass die erste Ungleichung recht einfach zu lösen ist, während die andere Ungleichung alles andere als einfach ist und man sie tatsächlich nicht lösen kann.
Wie man eine ungleichung löst
Im Allgemeinen finden wir die Lösung von Ungleichungen, indem wir zuerst eine zugehörige Gleichung lösen. Das Lösen der Ungleichung wird schwieriger, wenn die zugehörige Gleichung schwieriger zu lösen ist. Die folgenden Schritte werden Ihnen bei der Lösung helfen:
- Schritt 0: Vereinfachen Sie die Ausdrücke die an der Ungleichung beteiligt sind. Es ist fast immer einfacher, eine vereinfachte Ungleichung zu lösen als die ursprüngliche Ungleichung
- Schritt 1: Bestimmen Sie die Ungleichung, die Sie lösen wollen, und identifizieren Sie sorgfältig das Ungleichheitszeichen (>, ≥, <, ≤). Wenn Sie "=" haben, sollten Sie dann eine gleichungsrechner stattdessen
- Schritt 2: Anschließend schreiben Sie die zugehörige Gleichung auf, die Sie einfach dadurch erhalten, dass Sie das im vorherigen Schritt gefundene Ungleichheitszeichen durch das Gleichheitszeichen "=" ersetzen
- Schritt 3: Lösen Sie die zugehörige Gleichung. Bestimmen Sie die Lösung der Ungleichung auf der Grundlage der reellen Lösungen Ihrer zugehörigen Gleichung und notieren Sie alle Punkte, die den Ausdruck undefiniert machen könnten
- Schritt 4: Wenn Ihre zugehörige Gleichung keine reelle Lösung hat: In diesem Fall wissen Sie, dass die Gleichung niemals Null ist, zumindest nicht für reelle Werte. Unter der Annahme der Kontinuität sind dann entweder alle Punkte eine Lösung der Ungleichung oder keiner. Man wertet also die Ungleichung an einem beliebigen Punkt aus (z. B. x = 0), und wenn sie gilt, dann sind alle reellen Werte eine Lösung der Ungleichung, und wenn sie nicht gilt, dann gibt es keine reellen Lösungen
- Schritt 5: Nehmen wir schließlich an, dass es reelle Lösungen für die zugehörige Gleichung gibt. Wir nennen diese kritischen Punkte und fügen alle Punkte, an denen der Ausdruck undefiniert wird (Divisionen durch Null usw.), der Liste der kritischen Punkte hinzu
- Schritt 6: Wenn es nur einen kritischen Punkt gibt, den wir "a" nennen: Bewerten Sie die Ungleichung an einem beliebigen Punkt links von "a", und wenn sie gilt, wird das Intervall (-∞, a) Teil der Lösungsmenge sein. Lautet die Ungleichung "<=" or ">=", dann schließt man den Endpunkt (-∞, a) ein. Man macht einen ähnlichen Schritt für einen Punkt rechts von "a", und wenn die Ungleichung für ihn gilt, dann wird (-∞, a) Teil der Lösungsmenge sein
- Schritt 7: Ein ähnlicher Prozess wird durchgeführt, wenn mehr als ein kritischer Punkt existiert: Man nimmt zwei aufeinanderfolgende kritische Punkte, die wir 'a1' und 'a2' nennen: Bewerten Sie die Ungleichung an einem beliebigen Punkt zwischen a1 und a2, und wenn sie gilt, wird das Intervall (a1, a2) Teil der Lösungsmenge sein. Wenn die Ungleichung "<=" or ">=" lautet, dann schließen Sie die Endpunkte ein
Es scheint kompliziert zu sein, aber man muss einfach systematisch vorgehen. Wenn Ihre Ungleichung zum Beispiel \(\displaystyle x + \frac{1}{3} < x^2 \) lautet, dann ist die zugehörige Gleichung \(\displaystyle x + \frac{1}{3} = x^2 \), die leicht zu lösen ist, da es sich um eine Quadratische Gleisung .
Dann, im Rahmen der Analyse der kritischen Punkte (falls vorhanden), grafische Darstellung der Lösung der Ungleichung könnte die Dinge klarer machen. In einigen Algebra-Kursen lernen die Schüler, eine Tabelle zu verwenden, um zu verfolgen, was zwischen den kritischen Punkten passiert, was wirklich nützlich sein könnte.
Worin besteht der unterschied zu einem system von ungleichheiten?
Ein System von Ungleichungen besteht aus mehreren gleichzeitigen Ungleichungen, die gleichzeitig gelöst werden müssen. Es klingt schwieriger als die Lösung einer einfachen Ungleichung, weil es schwieriger ist. Wenn schon das Lösen von Ungleichungen mühsam sein kann, so gilt dies erst recht für Ungleichungssysteme.
Ein Beispiel für ein System von Ungleichungen ist unten dargestellt:
\[\displaystyle x + y < 1 \] \[\displaystyle 2x + y^2 \le 1 \]In dem obigen Beispiel haben Sie eine system der Ungleichheiten zu lösen ist. Dieses Ungleichungssystem besteht aus zwei Ungleichungen und zwei Unbekannten (x und y).
Wie Sie sich wahrscheinlich vorstellen können, kann das Lösen eines Systems von Ungleichungen im Allgemeinen schwierig sein. Meistens werden wir uns auf das Lösen von linearen Gleichungssystemen konzentrieren, die eng verbunden sind mit lösen eines Systems linearer Gleichungen

Vorteile der verwendung dieses ungleichheitsrechners mit schritten
Die meisten Ungleichheiten sind wirklich schwer zu lösen. Nur einige wenige von ihnen mit sehr spezifischen Strukturen eignen sich für eine Analyse. Die Mehrheit wird es nicht sein, also sollten Sie darauf vorbereitet sein.
- Wirbel 1: Sparen Sie viel Zeit: Das Lösen von Ungleichungen kann viel Zeit in Anspruch nehmen, da Sie zunächst die zugehörige Gleichung lösen und dann die kritischen Punkte analysieren müssen
- Wirbel 2: Stellen Sie sicher, dass Sie Ihr Bestes geben, um sie zu lösen: Wie Sie wahrscheinlich wissen, lassen sich nicht alle Gleichungen oder Ungleichungen leicht oder überhaupt lösen. Ein Taschenrechner mit Schritten wird den bestmöglichen Ansatz auf der Grundlage der erkannten Struktur versuchen
- Wirbel 3: Sie erhalten die Ergebnisse in übersichtlicher Form Schritt für Schritt. Einige Taschenrechner geben zwar die endgültige Antwort an, zeigen aber nicht die einzelnen Schritte an. Ein Diagramm, das die Lösungen darstellt, ist ebenfalls sehr nützlich
Während Sie sich einarbeiten, zeigt Ihnen ein Ungleichungsrechner, der Ihnen die schwere Arbeit abnimmt, den Weg, wie die Dinge gemacht werden, und Sie werden wahrscheinlich die Fähigkeiten erwerben, die Sie brauchen, um die Strukturen zu erkennen, die leichter zu bewältigen sind.
Gibt es einen praktischen nutzen für ungleichheiten?
Und ob! In den mathematischen Grundlagenfächern (Algebra und Calculus 101) liegt die Betonung auf Gleichheiten und Gleichungen. Die reale Welt ist voll von Prozessen, in denen wir nicht unbedingt Gleichungen haben, aber wir haben Ungleichheiten, die sich aus unteren oder oberen Grenzen ergeben, die durch physikalische Zwänge auferlegt werden.
Bestimmte fortgeschrittene mathematische Bereiche wie die Differentialgleichungen basieren auf Ungleichungen (die von den Fachleuten in manchen Zusammenhängen gerne als "Energieschätzungen" bezeichnet werden).
Die Bedeutung von Ungleichungen mag für Sie nicht offensichtlich sein, und die Notwendigkeit, sie zu lernen, ist auch nicht so dringend, aber in der Tat bilden Ungleichungen einen der Eckpfeiler der mathematischen Methodik, die zur Konstruktion von Theorien verwendet wird, auch wenn wir in den schönen Endergebnissen eher Gleichheiten sehen.

Beispiel: lösen von ungleichungen
Berechnen Sie die Lösung von: \(\frac{1}{3}x + \frac{5}{4} \ge \frac{1}{6}\)
Lösung: Wir müssen alle Terme der Ungleichung auf die linke Seite setzen (es könnte auch die rechte Seite sein, aber es ist eher üblich, die linke Seite zu verwenden):
\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6}\ge 0 \]Aus der obigen Ungleichung ergibt sich die zugehörige lineare Gleichung, die zunächst gelöst werden muss:
\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6} = 0 \]Schritt 0: In diesem Fall müssen wir zunächst die gegebene lineare Gleichung vereinfachen, und dazu führen wir die folgenden Vereinfachungsschritte durch:
Lösen der linearen gleichung
Setzt man \(x\) auf die linke Seite und die Konstante auf die rechte Seite, erhält man
\[\displaystyle \frac{1}{3}x = -\frac{13}{12}\]Löst man nun \(x\), indem man beide Seiten der Gleichung durch \(\frac{1}{3}\) dividiert, erhält man folgendes
\[\displaystyle x = \displaystyle \frac{ -\frac{13}{12}}{ \frac{1}{3}}\]und vereinfachen wir endlich die folgenden
\[\displaystyle x=-\frac{13}{4}\]Daher führt die Lösung von \(x\) für die gegebene lineare Gleichung zu \(x=-\frac{13}{4}\).
Analyse der kritischen punkte
Der einzige kritische Punkt, der gefunden wurde, ist \(-\frac{13}{4}\).
Auf dieser Grundlage müssen wir die folgenden Intervalle analysieren:
- Für das Intervall \(\left(-\infty, -\frac{13}{4}\right)\): Die linke Seite ist negativ, also ist \(\left(-\infty, -\frac{13}{4}\right)\) nicht Teil der Lösung.
- Für das Intervall \(\left(-\frac{13}{4}, \infty\right)\): Die linke Seite ist positiv, was bedeutet, dass \(\left(-\frac{13}{4}, \infty\right)\) Teil der Lösung ist.
Lösung der ungleichheit
Ausgehend von der angegebenen Ungleichung und der Analyse der kritischen Punkte finden wir, dass die Lösung der Ungleichung lautet: \(x \ge -\frac{13}{4}\).
In Intervallschreibweise wird die Lösung wie folgt geschrieben:
\[\left[-\frac{13}{4},\infty\right)\]Das diagramm der linearen Ungleichung der erhaltenen Lösung ist unten dargestellt
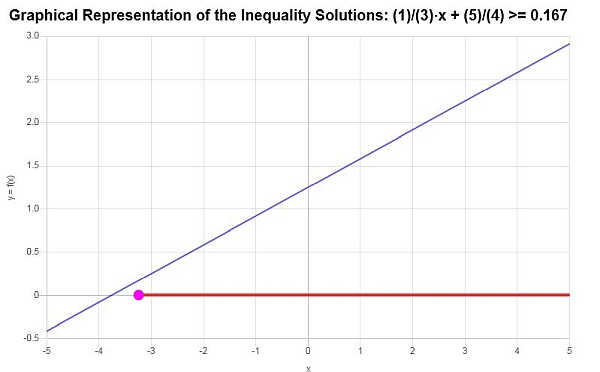
Beispiel: weitere ungleichheitsbeispiele
Finden Sie die Lösung der folgenden Aufgabe: \(\sin(x) > 0\)
Lösung: Wir haben die folgende trigonometrische Ungleichung, die es zu lösen gilt:
\[\sin\left(x\right) > 0\]Handhabung einer hilfsgleichung
Aus der obigen trigonometrischen Ungleichung ergibt sich die zugehörige Gleichung, die zunächst gelöst werden muss:
\[\sin\left(x\right)=0\]Lösen der trigonometrischen hilfsgleichung
so sind die Lösungen: \(x = \pi{}K\), für eine beliebige ganzzahlige Konstante \(K\).
Analyse der kritischen punkte
Ausgehend von den Lösungen der Hilfsgleichung wird die Liste der kritischen Punkte gefunden: \(\pi{}K\), für eine beliebige ganzzahlige Konstante \(K\).
Beachten Sie, dass es unendlich viele kritische Intervalle gibt, von denen wir einige im Folgenden analysieren:
- Für das Intervall \(\left(-3\pi{}, -2\pi{}\right)\): Die linke Seite ist negativ, also ist \(\left(-3\pi{}, -2\pi{}\right)\) nicht Teil der Lösung.
- Für das Intervall \(\left(-2\pi{}, -\pi{}\right)\): Die linke Seite ist positiv, was bedeutet, dass \(\left(-2\pi{}, -\pi{}\right)\) Teil der Lösung ist.
- Für das Intervall \(\left(-\pi{}, 0\right)\): Die linke Seite ist negativ, was bedeutet, dass \(\left(-\pi{}, 0\right)\) nicht Teil der Lösung ist.
- Für das Intervall \(\left(0, \pi{}\right)\): Die linke Seite ist positiv, was bedeutet, dass \(\left(0, \pi{}\right)\) Teil der Lösung ist.
- Für das Intervall \(\left(\pi{}, 2\pi{}\right)\): Die linke Seite ist negativ, also ist \(\left(\pi{}, 2\pi{}\right)\) nicht Teil der Lösung.
- Für das Intervall \(\left(2\pi{}, 3\pi{}\right)\): Die linke Seite ist positiv, was bedeutet, dass \(\left(2\pi{}, 3\pi{}\right)\) Teil der Lösung ist.
Und so verfahren wir für die gesamte Abfolge der Intervalle.
Teil lösungsintervalle
Auf der Grundlage der Analyse der gefundenen kritischen Punkte und der entsprechenden Intervalle, die durch aufeinanderfolgende kritische Punkte entstehen, können wir Folgendes als Teil der Lösung der Ungleichung identifizieren:
\[\left(-2\pi{}, -\pi{}\right) \cup \left(0, \pi{}\right) \cup \left(2\pi{}, 3\pi{}\right)\]In diesem Fall können wir annähernd verschiedene Lösungsbereiche identifizieren, wie die nachstehende Grafik zeigt. Die ungleichheitsgrapher ergibt die folgende grafische Darstellung der gefundenen Lösung:
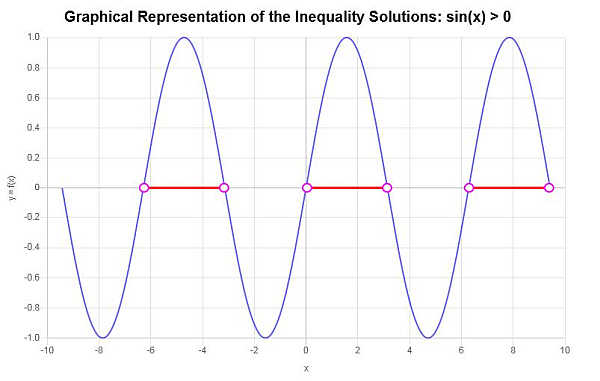
Beispiel: weitere ungleichheiten
Lösen Sie die quadratische Ungleichung \( x^2 - 2x > 6 \).
Lösung: Die Ungleichung, die wir lösen müssen, lautet
\[x^2-2x > 6\]Setzt man alle Terme der Ungleichung auf eine Seite, erhält man:
\[x^2-2x-6>0\]Hilfsgleichung
Wir erhalten die folgende Hilfsgleichung, die zunächst gelöst werden muss:
\[x^2-2x-6=0\]Wir haben einen Polynomausdruck auf der linken Seite, der \(\displaystyle deg(p) = 2\) ist, sein führender Koeffizient ist \(\displaystyle a_{2} = 1\) und sein konstanter Koeffizient ist \(\displaystyle a_0 = -6\).
Quadratische formel
In diesem Fall werden die Wurzeln nach der folgenden Formel berechnet:
\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\] \[\Rightarrow = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(1\right)\left(-6\right)}}{2\cdot 1} = \displaystyle \frac{2 \pm \sqrt{28}}{2}\]Also finden wir das:
\[ {x}_1 = \frac{2}{2}-\frac{1}{2}\sqrt{28}=\frac{2}{2}-\sqrt{7}=1-\sqrt{7}=-\sqrt{7}+1 \] \[{x}_2 = \frac{2}{2}+\frac{1}{2}\sqrt{28}=\frac{2}{2}+\sqrt{7}=1+\sqrt{7}=\sqrt{7}+1\]In diesem Fall hat die quadratische Gleichung \( \displaystyle x^2-2x-6 = 0 \) zwei reelle Wurzeln, die zu kritischen Punkten werden:
Analyse der kritischen punkte
Die Liste der gefundenen kritischen Punkte ist in aufsteigender Reihenfolge geordnet: \(-\sqrt{7}+1\), \(\sqrt{7}+1\).
Auf dieser Grundlage müssen wir die folgenden Intervalle analysieren:
- Für das Intervall \(\left(-\infty, -\sqrt{7}+1\right)\): Die linke Seite ist positiv, was bedeutet, dass \(\left(-\infty, -\sqrt{7}+1\right)\) Teil der Lösung ist.
- Für das Intervall \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\): Die linke Seite ist negativ, also ist \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\) nicht Teil der Lösung.
- Für das Intervall \(\left(\sqrt{7}+1, \infty\right)\): Die linke Seite ist positiv, was bedeutet, dass \(\left(\sqrt{7}+1, \infty\right)\) ein Teil der Lösung ist.
Finden der lösung der ungleichung
Ausgehend von der angegebenen Ungleichung und der Analyse der kritischen Punkte finden wir, dass die Lösung der Ungleichung lautet: \(x < -\sqrt{7}+1\) oder \(x > \sqrt{7}+1\).
In Intervallschreibweise wird die Lösung wie folgt geschrieben:
\[\left(-\infty,-\sqrt{7}+1\right) \cup \left(\sqrt{7}+1,\infty\right)\]Die Lösung der Ungleichung grafisch dargestellt:
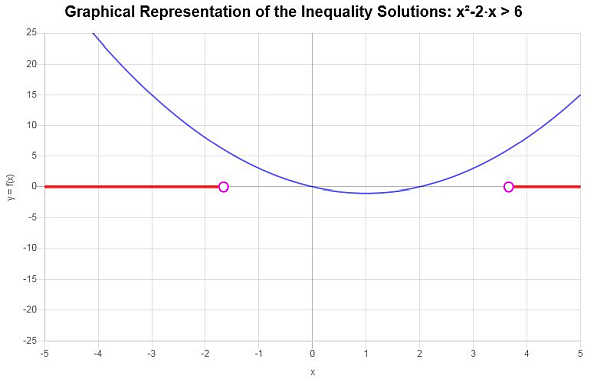
Mehr über ungleichheiten
Sie beginnen immer mit einer rechner für lineare Ungleichungen oder vielleicht eine rechner für quadratische Ungleichungen denn sie sind diejenigen, die garantiert eine Lösung bieten.
Dann, auch mit einer polynomiale Ungleichung könnte man schnell auf Sand stoßen, denn auch polynomiale Ungleichungen können knifflig oder sogar unmöglich mit elementaren Methoden exakt zu lösen sein.
Jede andere Art von Ungleichung hängt von ihrer Struktur und einer cleveren Ersetzung ab, die Sie sich ausdenken können.




