Mehr über polynomielle ungleichungen

Dieser Rechner kann Ihnen bei der Lösung von polynomialen Ungleichungen helfen, indem er Ihnen alle Schritte des Prozesses zur Berechnung der Lösung zeigt und Ihnen außerdem ein Ungleichheitsdiagramm zur Verfügung stellt, das die Lösung darstellt

Die von Ihnen angegebene Ungleichung kann etwas Einfaches sein wie "x^2 > 1" oder etwas Komplexeres wie "x^3 + 3x^2 + 3x + 1 > 0".

Sobald eine gültige polynomische Ungleichung angegeben ist, klicken Sie bitte auf die Schaltfläche "Berechnen", um die Lösung und alle Schritte angezeigt zu bekommen.

Bitte beachten Sie, dass nicht alle Polynome, die Sie angeben, sich für exakte Lösungen eignen. Je niedriger der Grad des Polynoms ist, desto wahrscheinlicher ist es, dass eine exakte Lösung der Ungleichung gefunden wird.

Was ist eine polynomielle ungleichung?

Eine polynomiale Ungleichung ist einfach eine Art von Ungleichung, bei der die beteiligten Ausdrücke polynomial sind und keiner der Terme ein nicht-polynomialer Ausdruck ist. Zum Beispiel

\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \displaystyle \frac{x^3}{3} \]

ist eine polynomiale Ungleichung, während

\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \sin(x) \]

ist ein nicht, weil der Term \(\sin x\) kein Polynom ist. Lösen von Ungleichungen ist im Allgemeinen ein schwieriger Prozess, aber für Polynome haben wir einen klaren Aktionsplan.

Wie löst man eine polynomiale ungleichung

• Schritt 1: Stellen Sie sicher, dass alle Terme Polynome sind. Ist dies nicht der Fall, können die spezifischen Methoden für Polynome nicht angewandt werden
• Schritt 2: Alles auf eine Seite legen, so dass auf der anderen Seite Null übrig bleibt
• Schritt 3: Ersetzen Sie das Ungleichheitszeichen durch "=" und lösen Sie die zugehörige Gleichung (dazu müssen Sie die Nullstellen eines Polynoms finden)
• Schritt 4: Sammeln Sie alle kritischen Punkte der Ungleichung, die in diesem Fall die reellen Nullstellen der Hilfsgröße Polynomielle Gleichung (in diesem Fall werden die komplexen Wurzeln nicht berücksichtigt)
• Schritt 5: Wenn es keine kritischen Punkte gibt, bedeutet dies, dass der Ausdruck das Vorzeichen nicht ändert, so dass die gesamte reelle Linie eine Lösung ist, oder es gibt keine Lösung. Um das zu überprüfen, wählt man einen beliebigen Punkt und schaut, ob er die Ungleichung erfüllt. Wenn ja, ist die gesamte reelle Linie die Lösung, wenn nicht, gibt es keine Lösung
• Schritt 6: Wenn es kritische Punkte gibt, konstruieren Sie Intervalle mit aufeinanderfolgenden kritischen Punkten (verwenden Sie -∞ als kritischen Anfangspunkt und ∞ als kritischen Endpunkt)
• Schritt 7: Prüfen Sie jedes dieser Intervalle und schauen Sie, ob ein Punkt darin die Ungleichung erfüllt. Wenn ja, ist das Intervall ein Teil der Lösung, wenn nicht, ist das Intervall nicht Teil der Lösung.

Der Schlüsselgedanke dabei ist, dass die kritischen Punkte und die daraus abgeleiteten Intervalle Intervalle sind, für die der Ausdruck das Vorzeichen nicht ändert, so dass entweder das gesamte Intervall eine Lösung ist oder kein Punkt im Intervall Teil der Lösung ist.

Polynomnullstellen und kritische punkte

Die Lösung polynomieller Ungleichungen ist u. a. deshalb möglich, weil es relativ einfach ist, polynomielle Ausdrücke auf kritische Punkte zu untersuchen, abgesehen davon, dass Polynome kontinuierliche Ausdrücke sind.

Es wird Ungleichheiten geben wie

\[\displaystyle \frac{\sin(x^2-1)}{x^3-1} < 1 \]

in denen es sehr viel schwieriger sein wird, kritische Punkte zu finden. lineare Ungleichungen ist es noch einfacher, kritische Punkte zu finden, aber das war's auch schon. Jede allgemeine Ungleichung hat ihre eigene Komplexität.

Anwendungen von polynomen im realen leben

Es gibt eine Vielzahl von Anwendungen für Polynome. Zum Beispiel gibt es in der Physik, wenn man Kinematik studiert, einige interessante Polynomausdrücke, die von den Newtonschen Gesetzen abgeleitet sind. Diese Ausdrücke können Bedingungen für die Position eines Körpers definieren, was zu einer polynomiellen Ungleichung führen könnte, um zu bestimmen, wann sich der Körper über einer bestimmten Höhe befindet, was sich beispielsweise in der Ballistik als entscheidend erweisen könnte.

Bei der Untersuchung von Differentialgleichungen können Sie auch Kippterme in der Gleichung finden, die von einer Potenz abhängen und eine Polynomstruktur haben, für die Sie einige fortgeschrittene Ungleichungen verwenden können, wie z. B. die Gronwall-Ungleichungen.

Beispiel: lösen polynomieller ungleichungen

Lösen: \(x^2 - x > \frac{1}{2}\)

Lösung: Wir müssen zunächst die folgende quadratische Gleichung \(\displaystyle x^2-x-\frac{1}{2}=0\) lösen:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{1 \pm \sqrt{\left(-1\right)^2-4\left(1\right)\left(-\frac{1}{2}\right)}}{2\cdot 1} = \displaystyle \frac{1 \pm \sqrt{3}}{2}\]

Also finden wir das:

\[ {x}_1 = \frac{1}{2}-\frac{1}{2}\sqrt{3}=-\frac{1}{2}\sqrt{3}+\frac{1}{2} \] \[{x}_2 = \frac{1}{2}+\frac{1}{2}\sqrt{3}=\frac{1}{2}\sqrt{3}+\frac{1}{2}\]

Analyse der kritischen punkte

Die Liste der gefundenen kritischen Punkte ist in aufsteigender Reihenfolge geordnet: \(-\frac{1}{2}\sqrt{3}+\frac{1}{2}\), \(\frac{1}{2}\sqrt{3}+\frac{1}{2}\).

Auf dieser Grundlage müssen wir die folgenden Intervalle analysieren:

- Für das Intervall \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\): Die linke Seite ist positiv, also ist \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) Teil der Lösung.

- Für das Intervall \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\): Die linke Seite ist negativ, was bedeutet, dass \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) nicht Teil der Lösung ist.

- Für das Intervall \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\): Die linke Seite ist positiv, was bedeutet, dass \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\) Teil der Lösung ist.

Lösung der ungleichheit

Ausgehend von der angegebenen Ungleichung und der Analyse der kritischen Punkte finden wir, dass die Lösung der Ungleichung lautet: \(x < -\frac{1}{2}\sqrt{3}+\frac{1}{2}\) oder \(x > \frac{1}{2}\sqrt{3}+\frac{1}{2}\).

In Intervallschreibweise wird die Lösung wie folgt geschrieben:

\[\left(-\infty,-\frac{1}{2}\sqrt{3}+\frac{1}{2}\right) \cup \left(\frac{1}{2}\sqrt{3}+\frac{1}{2},\infty\right)\]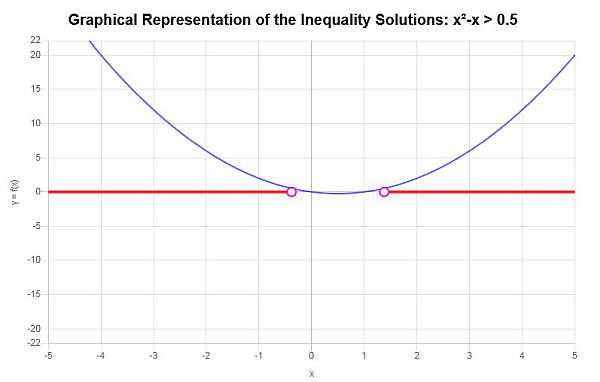

womit die Berechnung abgeschlossen ist.

Beispiel: polynom höheren grades

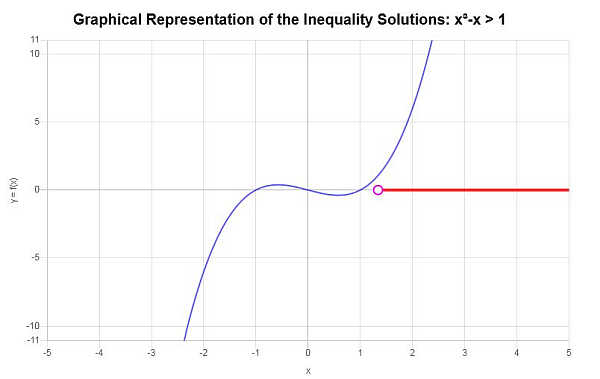
Lösen Sie die folgende Ungleichung: \(x^3 - x > 1\)

Lösung:

Um \(x^3-x > 1\) zu lösen, legen wir zunächst alles auf eine Seite:

\[x^3-x-1> 0\]

Daraus ergibt sich nun die zugehörige Gleichung, die zuerst gelöst werden muss, nämlich \(x^3-x-1=0\). Beachten Sie, dass der Grad \(\displaystyle deg(p) = 3\), der führende Koeffizient \(\displaystyle a_{3} = 1\) und der konstante Koeffizient \(\displaystyle a_0 = -1\) ist.

Versuch einer rationalen wurzel

Wir werden zunächst versuchen, einfache rationale Wurzeln zu finden, und zwar mit dem Satz von der rationalen Null.

Die nächste Aufgabe besteht darin, die ganzzahligen Zahlen zu finden, die den führenden Koeffizienten \(a_{3}\) und den konstanten Koeffizienten \(a_0\) teilen, die verwendet werden, um unsere Kandidaten als Nullstellen der Polynomgleichung zu konstruieren.

▹ Die Teiler von \(a_{3} = 1\) sind: \(\pm 1\).

▹ Die Teiler von \(a_0 = -1\) sind: \(\pm 1\).

Dividiert man also jeden Teiler des konstanten Koeffizienten \(a_0 = -1\) durch jeden Teiler des führenden Koeffizienten \(a_{3} = 1\), so erhält man die folgende Liste von Kandidaten für Wurzeln:

\[\pm \frac{ 1}{ 1}\]

Jetzt müssen alle Kandidaten getestet werden, um festzustellen, ob sie eine Lösung sind.Das Folgende erfolgt aus dem Testen der einzelnen Kandidaten:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle -1^3-\left(-1\right)-1 & = & \displaystyle -1 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle 1^3-1-1 & = & \displaystyle -1 \ne 0 \\\\ \end{array}\]

Da wir jedoch keine rationalen Wurzeln durch Inspektion gefunden haben, können wir die Faktorisierung mit Elementarmethoden nicht weitermachen, sodass der Prozess hier stoppt.

OPTIONAL : Es handelt sich um ein Polynom vom Grad \(3\), für das es insgesamt \(3\) Wurzeln gibt, auch wenn einige komplex sein könnten, aber in diesem Fall wurden mit elementaren Methoden weniger als \(3\) Lösungen gefunden.

Mit Hilfe fortschrittlicher Methoden der kubischen Gleichung lässt sich feststellen, dass die vollständige Lösungsmenge folgendermaßen aussieht:

\[x_1=\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\]
\[x_2=\frac{\frac{1}{6}\cdot \left(-3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}+i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]
\[x_3=\frac{\frac{1}{6}\cdot \left(3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]

Analyse der kritischen punkte

Der einzige kritische Punkt, der gefunden wurde, ist \(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\).

Auf dieser Grundlage müssen wir die folgenden Intervalle analysieren:

- Für das Intervall \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\): Die linke Seite ist negativ, also ist \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\) nicht Teil der Lösung.

- Für das Intervall \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\): Die linke Seite ist positiv, was bedeutet, dass \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\) Teil der Lösung ist.

Lösung der ungleichheit

Ausgehend von der angegebenen Ungleichung und der Analyse der kritischen Punkte finden wir, dass die Lösung der Ungleichung lautet: \(x > 1.3247180451128\).

In Intervallschreibweise wird die Lösung wie folgt geschrieben:

\[\left(1.3247180451128,\infty\right)\]

Grafisch:

Weitere rechner für ungleichheit

Lösen von Ungleichungen (Ausgeschlossen von lösungen für Gleichungen finden ) ist eine der gebräuchlichsten Operationen in der Mathematik, und zwar in allen Bereichen.

Das Lösen von Ungleichungen ist in der Regel mühsam, und im Allgemeinen gibt es keine Regel, um sie zu lösen. Lösen polynomieller Ungleichungen ist eine der wenigen Ausnahmen, bei denen wir eine Reihe von Schritten befolgen können, um die Lösungen zu finden, aber dennoch können wir scheitern, weil Polynome höheren Grades schwer zu handhaben sind. In der Tat ist es wirklich unmöglich Polynomwurzeln Funde über Grad 5 nach einer allgemeinen Regel (Abelscher Satz).