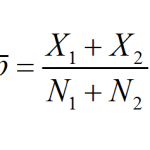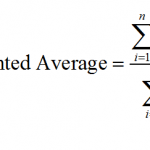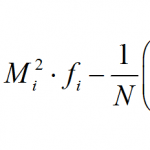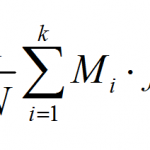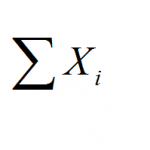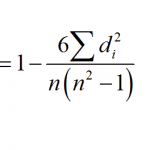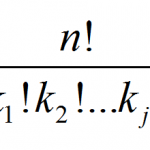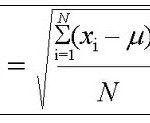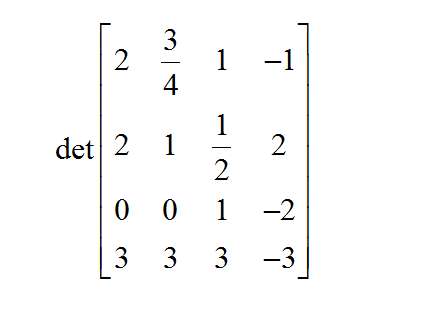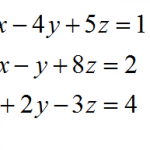MathCracker offers a wide variety of Statistics calculators, that will perform step-by-step calculations for you. Such calculators come in all forms and shapes, some are very simple
(such as for example, simple combinatorial coefficient calculations) and some conduct elaborate calculations
(such as some non-parametric statistical test).
One great advantage of our online calculators/solvers is that we attempt to provide, whenever possible, a complete step-by-step detail of how to arrive to the required solution.
We believe that showing all the steps of how one has arrived to the solution is the best way (and sometimes the only way) to learn a subject.
There are many probability calculators (including calculators for the most common distributions, such as the normal, the t-distribution, the F-distribution, etc), a
complete selection of hypothesis test solvers, for both parametric and non-parametric tests.
How to Find the Stats Calculator I'm looking For?
Check our list below of Stats solvers, or you can also use the search box provided, to find the exact calculator you are looking for. Each solver will come with clear instructions on how the solver should be used. Also, some calculators will have available videos that will help you to proceed if you are having troubles.
Our goal is to have the most complete collection of math calculators online, and when I say Math I mean that we don't only have stats calculators but also Algebra, Probability, and many other subjects. If there is a solver that you don't find in our site and you would like to see included here, please do not hesitate to contact us.
Check the Stats Calculators We have Available
Instructions: This Negative Predictive Value Calculator computes the negative predictive value (NPV) of a test, ...
Instructions: This Positive Predictive Value Calculator computes the positive predictive value (PPV) of a test, ...
Instructions: This Specificity Calculator computes the specificity of a test, showing step-by-step all calculation. To ...
Instructions: This Sensitivity Calculator computes the sensitivity of a test, showing all the steps. To that end, ...
Instructions: Use this Covariance Calculator to find the covariance coefficient between two variables (X) and (Y) that ...
Instructions: This Deviation Score Calculator will compute the deviation with respect to the mean for a sample of data ...
Instructions: Use this one to calculate the percentile from the mean and standard deviation. Please provide the ...
Instructions: This Degrees of Freedom Calculator will calculate the number of degrees of freedom for paired samples of ...
Instructions: This Degrees of Freedom Calculator will indicate the number of degrees of freedom for two samples of, ...
Instructions: This Degrees of Freedom Calculator will indicate the number of degrees of freedom for one sample of, ...
Instructions: This interquartile range calculator will calculate the IQR, showing step-by-step calculations, for a ...
Instructions: This decile calculator will calculate a decile that you specify, showing step-by-step calculations of ...
Instructions: This quartile calculator will calculate a quartile you specify, showing step-by-step calculations, for a ...
Instructions: You can use this Pooled Proportion Calculator to compute the pooled proportion for two sample. ...
Instructions: Use this Weighted Average Calculator to compute the weighted average of a set of values (X) and their ...
Instructions: Use this Ogive Graph Maker to construct a cumulative frequency polygon based on a sample provided in the ...
Instructions: Use this Frequency Polygon Graph Maker to construct a frequency polygon based on a sample provided in ...
Instructions: Use this Sample Variance of Grouped Data Calculator to find the sample variance for the case of grouped ...
Instructions: Use this Sample Mean of Grouped Data Calculator to find the sample mean when you have grouped data, in ...
Instructions: Use this Coefficient of Determination Calculator to compute the coefficient of determination ((R^2)) ...
Instructions: Use this Residual Plot Grapher to construct a residual plot for the value obtained with a linear ...
Instructions: Use this Regression Predicted Values Calculator to find the predicted values by a linear regression ...
Instructions: Use this Regression Residuals Calculator to find the residuals of a linear regression analysis for the ...
Instructions: The following Pie Chart Maker for raw data creates a pie chart based on sample data you provide in the ...
Instructions: Use this sample min calculator to get the minimum value (the smallest value) from all the values in a ...
Instructions: Use this Relative Frequency Graph Maker to create a bar chart with relative frequencies associated to ...
Instructions: Use Markov's Inequality calculator to estimate an upper bound of the probability of an event (Pr(X ge)) ...
Instructions: Use this Frequency Table Calculator to construct a frequency table associated with the sample provided ...
Instructions: Use this Summation Calculator to get the sum of all the values from a sample provided in the form below. ...
Instructions: Use this Standard Normal Distribution Probability Calculator to compute probabilities for the Z ...
Instructions: Use this step-by-step Bayes Rule Calculator to reverse conditional probabilities using Bayes' Theorem. ...
Instructions: This Contingency Table Calculator will help you create a contingency table (also known as crosstable) ...
Instructions: Use this Spearman's Critical Correlation Calculator to find the critical values for Spearman's ...
Instructions: Use this Multinomial Coefficient Calculator to compute showing all the steps a multinomial coefficient ...
Instructions: Use this Multiple Correlation Coefficient Calculator for a multiple linear regression. Please input the ...
Instructions: Use this step-by-step calculator for a confidence interval for the difference between two Means, for ...
Instructions: Use this step-by-step Confidence Interval for Mean Calculator, with unknown population variance, by ...
Instructions: Use this step-by-step Confidence Interval for Mean Calculator, with known population variance, by ...
Instructions: Use this step-by-step calculator for a confidence interval for the difference between two Means, for ...
Instructions: Use this step-by-step Confidence Interval for the Difference Between Proportions Calculator, by ...
Instructions: Use this step-by-step Confidence Interval for Ratio of two Variances Calculator ((displaystyle frac ...
Instructions: Use this step-by-step Confidence Interval for Proportion Calculator, by providing the sample data in the ...
Instructions: Use this step-by-step Confidence Interval for Variance and Standard Deviation Calculator, by providing ...
Instructions: Use this Sample Variance Calculator to compute, showing all the steps the sample variance (s^2), using ...
Instructions: Use this Z-score to T-score Calculator to transform a z-score into a T-score (this is capital "T"). ...
Instructions: Use this residual sum of squares to compute (SS_E), the sum of squared deviations of predicted values ...
Instructions: Use this regression sum of squares calculator to compute (SS_R), the sum of squared deviations of ...
Instructions: Use this Raw Score Calculator to transform a z-score into a raw score. Please provide the information ...
Instructions: This Sum of Squares Calculator will help you compute the sum of squares associated to a set of sample ...
Instructions: This Percentile to Z-score Calculator will compute the z-score associated to a given percentile that is ...
Instructions: This Z-Score to Percentile Calculator will compute the percentile associated to a Z-score that is ...
Instructions: Use this Law of Multiplication calculator to compute the probability (Pr(A cap B)). Please provide the ...
Instructions: Use this Law of Addition calculator to compute the probability (Pr(A cup B)). Please provide the ...
Instructions: Use this Conditional Probability calculator to compute the conditional probability (Pr(A | B)). Please ...
Instructions: Use this step-by-step Total Probability Rules calculator to compute the probability of an event (A), ...
Instructions: This calculator allows you to use the Maximax criterion (also known as optimistic criterion) to make a ...
Instructions: Use this prediction interval calculator for the mean response of a regression prediction. Please input ...
Instructions: Use this confidence interval calculator for the mean response of a regression prediction. Please input ...
Instructions: Enter the sample data below and this calculator will provide step-by-step calculation of the Five Number ...
Instructions: Use this calculator to compute Chi-Square distribution probabilities. Please type in the number of ...
Instructions: Use this calculator to compute F-distribution probabilities. Please type in the degrees of freedom ) ...
Instructions: Enter the sample data below and this calculator will provide step-by-step calculation of the Mean ...
Instructions: Use this calculator to compute the adjusted R-Squared coefficient from the R-squared coefficient. Please ...
Instructions: Use this calculator to compute the adjusted R-Squared coefficient for a multiple linear regression. ...
Instructions: Use this calculator to compute the adjusted R-Squared coefficient for a simple linear regression. Please ...
Instructions: Use this calculator to estimate the effect of a finite population on the calculation of the standard ...
Instructions: Use this calculator to compute probabilities associated to the sampling distribution of the sample ...
Instructions: Use this McNemar test calculator calculator to compute the results of applying McNemar's procedure to ...
Instructions: Enter the sample data below and this calculator will provide step-by-step calculation of the Mean ...
Instructions: Enter the sample data below and the solver will provide step-by-step calculation of the Mid-Range, using ...
Instructions: You can use step-by-step calculator to get the mean ((mu)) and standard deviation ((sigma)) associated ...
Instructions: You can use this Multiple Linear Regression Calculator to estimate a linear model by providing the ...
Instructions: You can use this Multiple Linear Regression Calculator to estimate a linear model by providing the ...
Instructions: You can use this Probability to Odds Calculator to compute the odds for the occurrence of an event, ...
Instructions: You can use this Odds to Probability Calculator to compute the probability of an event ((p)), given the ...
Instructions: Use this Hypergeometric Probability Calculator to compute hypergeometric probabilities using the form ...
Instructions: This tool will show you step-by-step calculations of the semi-partial correlations for three variables ...
Instructions: You can use this Partial Correlation Calculator to compute the corresponding partial Correlations for ...
Instructions: In order to use this Coefficient of Variation Calculator, please provide the sample data below and this ...
Instructions: Use this Correlation Coefficient Significance Calculator to enter the sample correlation (r), sample ...
Instructions: This correlation matrix calculator will provide you with a correlation matrix for a given set of. ...
Instructions: Use this outlier calculator by entering your sample data. This calculator will show you all the steps to ...
Instructions: Use this Normal Probability Plot maker by entering the sample data below and this statistics calculator ...
Instructions: Compute the inverse cumulative score for the standard normal probability distribution. Provide a ...
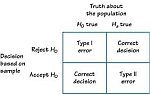
Instructions: This statistical power calculator computes, showing all the steps, the minimum required sample size ()) ...
Instructions: This power calculator computes, showing all the steps, the probability of making a type II error ()) ...
Instructions: This percentile calculator for grouped data will calculate a percentile you specify, showing step-by, ...
Instructions: This percentile calculator will calculate a percentile you specify, showing step-by-step, for a sample ...
Instructions: This effect size calculator for the t-statistic allows you to compute the value of (r^2) (r-squared) if ...
Instructions: This Chebyshev's Rule calculator will show you how to use Chebyshev's Inequality to estimate ...
Instructions: This Empirical Rule calculator will show you how to use the Empirical Rule to compute some normal ...
Instructions: You can use this permutation coefficient calculator to compute (P_{n,k}), for two given integers (n)( ...
Instructions: You can use this combinatorial coefficient calculator to compute "n choose k", or ( C_{n,k}), for two ...
Instructions: You can use this factorial calculator to compute the factorial of an integer number (n). Type the: ...
Instructions: You can use this Spearman Correlation Calculator tool to compute Spearman's Correlation Coefficient for ...
Instructions: This calculator computes the pooled variance and standard deviation for two given sample standard ...
Instructions: This Effect Size Calculator will compute the value of Cohen's d for you, showing all the steps. Please ...
Instructions: This Gamma Coefficient Calculator computes the value of Gamma, which measures the strength of the ...
Instructions: This calculator conducts a Sign Test. Please select the null and alternative hypotheses, enter the ...
Instructions: The following graphical tool creates a bar graph based on the data you provide in the boxes below. All ...
Instructions: Use this Harmonic Mean Calculator by entering the sample data below and the solver will provide step-by ...
Instructions:The following graphical tool creates a Stem-and-Leaf on the data you provide in the box below. Type the ...
Instructions: This calculator conducts a t-test for one population mean ((sigma)), with unknown population standard ...
Instructions: This calculator conducts a Chi-Square test of independence. Please first indicate the number of columns ...
Instructions: Use this Mean and Standard Deviation Calculator by entering the sample data below and the solver will ...
Instructions: This calculator conducts a t-test for two paired samples. This test applies when you have two samples ...
Instructions: Use this Confidence Interval Calculator for the population mean (mu), in the case that the population ...
Instructions: This calculator finds the minimum sample size required to estimate a population proportion ((p)) within ...
Instructions: This calculator conducts a Wilcoxon Rank Sum test for two independent samples. This test applies when ...
Instructions: Enter the sample correlation (r), sample size (n) and the significance level (alpha), and the solver ...
Instructions: This calculator conducts One-Way ANOVA for a group of samples, with the purpose of comparing the ...
Instructions: This calculator conducts a Wilcoxon Signed-Ranks Test for two paired samples. This test applies when you ...
Instructions: This calculator computes the value of Cramer's V. Please first indicate the number of columns and rows ...
Instructions: You can use this Phi Coefficient calculator by first indicating the number of columns and rows for the ...
Instructions: The following graphical tool creates a box plot on the data you provide in the boxes. You can type one ...
Instructions: This calculator conducts Kruskal-Wallis Test, which is non-parametric alternative to the One-Way ANOVA ...
Instructions: Use this T-Distribution Probability Calculator to Compute t-distribution probabilities using the form ...
Instructions: Compute critical Chi-Square values for the Chi-Square distribution using the form below. Please type the ...
Instructions: This calculator computes the value of Lambda, which measures the strength of the association between two ...
Instructions: Use this Time Series Plot Maker to create a time series plot using the form below. All you have to do is ...
Instructions: This calculator conducts a Z-test for one population mean ((mu)), with known population standard ...
Instructions: Use this Descriptive Statistics Calculator to enter the sample data below and the solver will provide ...
Instructions: Compute Poisson distribution probabilities using the form below. Please type the population mean (; ...
Instructions: This calculator conducts a Z-test for one population proportion (p). Please select the null and ...
Instructions: Compute exponential distribution probabilities using the form below. Please type the population mean ( ...
Instructions: This calculator computes the Relative Risk for a 2x2 crosstabulation, which measures the ratio of the ...
Instructions: Use our Binomial Probability Calculator to compute binomial probabilities using the form below. Please ...
Instructions: The following graphical tool creates a histogram based on the data you provide in the boxes below. All ...
Instructions: Compute critical t values for the t-distribution using the form below. Please type significance level ...
Instructions: The following graphical tool creates a box plot on the data you provide in the boxes. You can type one ...
Instructions: This calculator conducts Kruskal-Wallis Test, which is non-parametric alternative to the One-Way ANOVA ...
Instructions: Use this T-Distribution Probability Calculator to Compute t-distribution probabilities using the form ...
Instructions: Enter the sample correlation (r), sample size (n) and the significance level (alpha), and the solver ...
Instructions: This calculator conducts One-Way ANOVA for a group of samples, with the purpose of comparing the ...
Instructions: This calculator conducts a Wilcoxon Signed-Ranks Test for two paired samples. This test applies when you ...
Instructions: This calculator computes the value of Cramer's V. Please first indicate the number of columns and rows ...
Instructions: You can use this Phi Coefficient calculator by first indicating the number of columns and rows for the ...
Instructions: Compute critical z-values for the normal distribution probabilities using the form below. In order to do ...
Instructions: Use our Binomial Probability Calculator to compute binomial probabilities using the form below. Please ...
Instructions: The following graphical tool creates a histogram based on the data you provide in the boxes below. All ...
Instructions: Compute critical t values for the t-distribution using the form below. Please type significance level ...
Instructions: The following graphical tool creates a box plot on the data you provide in the boxes. You can type one ...
Instructions: This calculator conducts Kruskal-Wallis Test, which is non-parametric alternative to the One-Way ANOVA ...
Instructions: Use this T-Distribution Probability Calculator to Compute t-distribution probabilities using the form ...
You can use this step-by-step calculator of confidence interval for the Correlation Coefficient for two variables X and Y. All you have to do is type your X and Y data in the spreadsheet below, and specify the confidence level.
You can paste data directly from Excel, if that is how you have your data.
Instructions:
You can use this calculator of confidence interval for the Correlation Coefficient in the case you already know
the sample correlation. So, all you have to do is to provide the sample correlation \(r\), the sample size \(n\)
and specify the confidence level in the form below.
Instructions:
Use this calculator to generate an elementary row matrix that will multiply row \(p\) by a factor \(a\), and row \(q\)
by a factor \(b\), and will add them, storing the results in row \(q\). Please provide the required information to
generate the elementary row matrix.
The notation you follow is \(a R_p + b R_q \rightarrow R_q \)
Instructions:
Use this Matrix Determinant calculator, to compute the given determinant of a matrix, showing all the steps. First, click on one of the
buttons below to change the dimension of the matrix, if needed.
Then, click on the first cell and type the value, and move around the matrix by pressing "TAB" or by clicking on the corresponding cells, to
define ALL the matrix values.
Instructions:
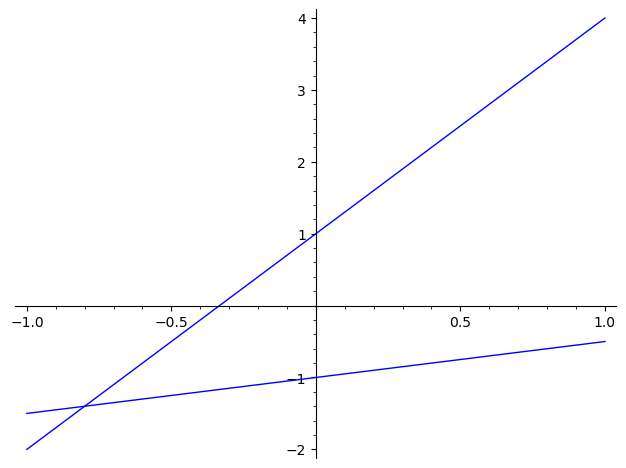
Use this graphing tool to plot the graph of two lines that you provide. Please type two linear equations.
Instructions:
Use this calculator to solve a system of two linear equations using the substitution method, showing all the steps. Please type two valid linear equations in the boxes provided
below:
Instructions:
Use this calculator to solve a system of linear equations using the elimination method, with all the steps shown .
Please provide two valid linear equations in the boxes provided
below:
Instructions:
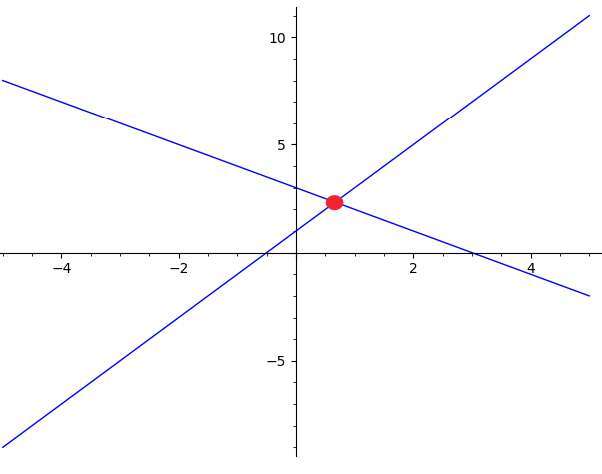
Use this calculator to solve a system of two linear equations using the graphical method. Please type two valid linear equations in the boxes provided
below:
Instructions:
Use this calculator to work on a two-samples t-test, showing all the steps. In order to run the test, you need two provide
two independent samples in the spreadsheet below. You can either type the data or simply paste them from Excel.
Instructions:
Use this two-sample z-test calculator to get the results of a t-test when two samples are provided, along
with the corresponding population standard deviations. Please provide the required information below
In case you have any suggestion, or if you would like to report a broken solver/calculator, please do not hesitate to contact us.