More About the Correlation Matrix

A Correlation Matrix is a table in which the pairwise correlations between several variables are conveniently organized in a matrix form. The value in the ith row an jth column corresponds to the correlation between the variables \(X_i\) and \(X_j\).

In simple words, the correlation matrix is a summary of all the correlations that can be found for a set of variables, for which sample data is available.

Correlation calculation is crucial, because it is the previous step need to apply a linear regression calculator to find the Least Squares Model. But this should be attempted only when the correlation is found to be significant.

Correlation Matrix Formula

Since \(corr(X_i, X_j) = corr(X_j, X_i)\), then the correlation matrix is symmetric, and for that reason, in order to not to be redundant, the correlation matrix only reports the values from the diagonal and up. For other correlation operations, you can compute a correlation coefficient showing all the steps, or you can use this critical correlation calculator .

How do You compute a correlation Matrix

In order to understand how to compute a correlation matrix, you need to know first how to calculate Pearson's correlation, because the correlation matrix is simply the matrix of the correlations between all possible pairs of variables.

In order to proceed with the calculation of the correlation matrix, you need to follow these steps:

Step 1: List the variables you have, say X1, X2, ..., etc. Each of these variables has a sample associated to it

Step 2: Take the ith and jth variables from your list, Xi and Xj, and compute the correlation coefficient for them. Call it \(r_{ij}\)

Step 3: Take the value \(r_{ij}\) and that will the value of the row i, column j of the correlation matrix

Correlation values close to 1 or -1 indicate strong linear associations, suggesting that a linear regression calculator (or a multiple linear regression, depending on how many predictors you have).

How do you use a correlation matrix?

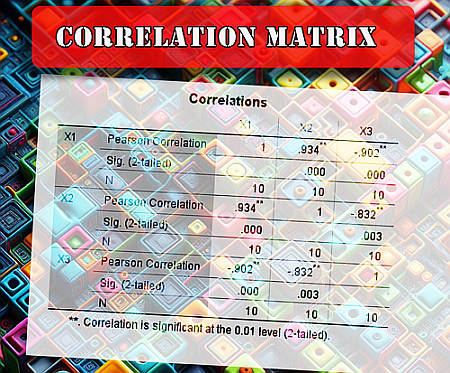
This is a point that needs to be addressed, as often times a correlation matrix can be given in different formats. The correlation matrix will be a table with the same number of rows and columns, where the name of the variables will appear in the corresponding rows and column.

So then, if you the first variable is \(X_1\), then the first row will give you the correlation coefficient of \(X_1\) and each of the other variables. And if the second variable is \(X_2\), then the second row will give you the correlation coefficient of \(X_2\) and each of the other variables, and so on.

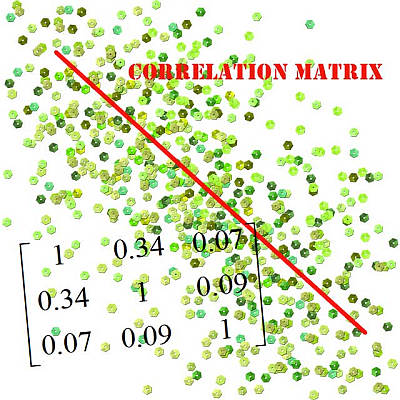
By based on the way this is defined, in row 1, column 1 you have the correlation of \(X_1\) with itself, which is 1, then in row 2, column 2 you have the correlation of \(X_2\) with itself, which is also 1, and so forth.

So what is happening is that you will find that the diagonal of the correlation matrix has only 1's in it, always. Since that is something that happens always, often times the correlation matrix calculated will omit the diagonal (because we already knows it has 1's in it, so what is the point in writing it explicitly).

But there is another thing to observe: the correlation between \(X_1\) and \(X_2\) is the same as the correlation between \(X_2\) and \(X_1\), so the correlation matrix is symmetric, so the values below the diagonal mirror what you have above the diagonal.

That is why very often you see a correlation matrix with values reported only above the diagonal (or below) only, because we know that diagonal is 1, and we know the values below the diagonal are a mirror reflection of the values above the diagonal.