Gráfico de polinomios

Usa esta calculadora si necesitas ayuda para graficar una función polinomial. El proceso es sencillo: solo tienes que teclear la función polinomial que quieres graficar. Puede escribir algo como '3x^3 + x - 1', o puede comenzar con el nombre de la función, como 'p(x) = 3x^3 + x - 1'.

Los coeficientes del polinomio proporcionado no tienen que ser necesariamente enteros, pueden ser fracciones o cualquier expresión algebraica válida. El polinomio que proporciones puede venir simplificado o no, no importa.

Luego, una vez proporcionado el polinomio, opcionalmente puede determinar los rangos de valores de x que se graficarán, y luego hace clic en "Calcular", y en breve, se mostrarán todos los pasos del proceso.

funciones polinómicas son uno de los objetos más importantes que encontrarás tanto en Álgebra como en Cálculo. Además, los polinomios generan la necesidad de resolver ecuaciones polinómicas, que tienen muchas aplicaciones en todas partes, en todos los aspectos de la vida, incluso más allá de las matemáticas.

Conceptos básicos de las funciones polinómicas

Recordemos que una función polinomial tiene la siguiente forma:

\[\displaystyle p(x) = a_0 + a_1 x + a_2 x^2 + .... + a_n x^n \]

donde asumimos que \(a_n \ne 0\), y decimos que el grado del polinomio en este caso es igual a \(n\), y el coeficiente principal es \(a_n\). La forma sencilla de definir el grado de un polinomio es que corresponde a la potencia más alta presente en la expresión del polinomio.

Por ejemplo, \(p(x) = 3x^2 + 2x - 1\) es un polinomio de grado 2, y su coeficiente principal es 3. Ahora, \(p(x) = \sin(3x^2 + 2x - 1)\) NO es un polinomio, por ejemplo.

¿cómo hacer gráficas de polinomios?

Graficar polinomios en principio muestra lo mismo que graficar cualquier otra función. Si tuviera que hacerlo a mano, tabularía varios valores para x e y, y trazaría una curva que más o menos pasaría por los puntos que obtiene en su tabla.

Naturalmente, este método es un poco primitivo porque, en general, no podemos conocer necesariamente la gráfica completa de una función simplemente conociendo un montón de puntos que estamos tabulando.

Afortunadamente, para los polinomios la tarea es un poco más fácil y, en realidad, podemos saber mucho sobre su gráfico conociendo su coeficiente principal y su grado.

Pasos para graficar funciones polinómicas

La gráfica de un polinomio depende en última instancia del coeficiente específico de cada polinomio. Pero podemos hacer algunas afirmaciones sólidas sobre el comportamiento final de un polinomio y la existencia de raíces reales.

Recordemos que el comportamiento final de un polinomio es el comportamiento del polinomio cuando x es muy grande y negativo, y cuando x es muy grande y positivo.

• Paso 1: Identifique la función polinomial y simplifique si puede, ya que es más fácil graficar expresiones que se simplifican
• Paso 2: ¿Conoces las raíces del polinomio? Si esas son raíces reales, conoce los puntos donde el polinomio cruza el eje x, lo que le brinda una referencia gráfica sólida
• Paso 3: Si el grado del polinomio es impar, entonces el comportamiento final será opuesto para valores de x negativos grandes y valores de x positivos grandes. Si el coeficiente principal es positivo, para valores de x negativos grandes, el polinomio será muy grande y negativo, y para valores de x positivos grandes, el polinomio será muy grande y positivo. Si el coeficiente principal es negativo, para valores de x negativos grandes, el polinomio será muy grande y positivo, y para valores de x positivos grandes, el polinomio será muy grande y negativo.
• Paso 4: Si el grado del polinomio es par, entonces el comportamiento final será el mismo para valores de x negativos grandes y valores de x positivos grandes. Si el coeficiente principal es positivo, para valores de x positivos y negativos grandes, el polinomio será muy grande y positivo. Si el coeficiente principal es negativo, para valores de x negativos y positivos grandes, el polinomio será muy grande y negativo
• Paso 5: Si el grado del polinomio es impar, el polinomio cruzará al menos una vez el eje x (por lo que tiene al menos una raíz real), mientras que para un grado par, el polinomio no necesariamente cruzará el eje x
• Paso 6: Un polinomio de grado n cruzará el eje x como máximo n veces. Por ejemplo, un polinomio de 4 grado 4 puede cruzar el eje x como máximo 4 veces

Entonces, por ejemplo, un polinomio cúbico puede cruzar el eje x como máximo 3 veces, pero no tiene por qué hacerlo.

Calculadora gráfica

¿Cuáles son las ventajas de usar una calculadora gráfica? Muchos. Eso no quiere decir que no sea una buena habilidad tener la capacidad de dibujar con precisión un polinomio usando lápiz y papel.

\[\displaystyle \frac{a}{b} \times \frac{c}{d} = \displaystyle \frac{ac}{bd} \]

• Ventaja 1: Te aseguras de obtener una representación precisa del gráfico real del polinomio
• Ventaja 2: Puede usarlo para verificar su propio trabajo, para asegurarse de que estaba siguiendo los pasos correctos
• Ventaja 3: Una buena calculadora con elegir una ventana apropiada para mostrar los aspectos más relevantes del gráfico

Un buen gráfico puede decirte mucho sobre las propiedades de una función, y lo mismo ocurre con un polinomio. Graficar polinomios puede ayudarte a visualizar realmente qué tipo de raíces tiene el polinomio.

Consejos y trucos

Tenga cuidado con la lectura excesiva de lo que ve en un gráfico de polinomios. No se puede decir mucho acerca de las raíces con multiplicidad, por lo que nada reemplaza la función real.

Si quieres probar otros tipos de funciones, prueba esto gráfico de función herramienta.

Ejemplo: graficar funciones polinómicas

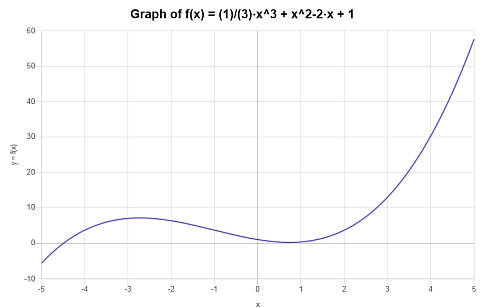
Grafica el siguiente polinomio: \(p(x) = \frac{1}{3} x^3 + x^2- 2x +1 \)

Solución: Se nos proporciona la siguiente expresión polinomial que necesitamos calcular: \(\displaystyle \frac{1}{3} x^3 + x^2- 2x +1\).

La expresión proporcionada es irreducible, por lo que no hay nada que simplificar.

El siguiente gráfico se obtiene para la expresión polinomial dada en el intervalo \([-5, 5]\):

Ejemplo: gráfico de polinomios

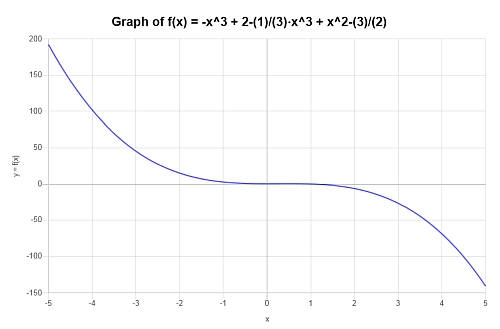
Simplifica y grafica: \(p(x) = x^4 - x^3 + 2 - \frac{1}{3}x^3 + x^2 - \frac{3}{2}\)

Solución: Ahora, necesitamos trabajar con: \(\displaystyle -x^3+2-\frac{1}{3}x^3+x^2-\frac{3}{2}\).

Se obtiene la siguiente simplificación:

lo que concluye el proceso de simplificación de polinomios.

Entonces, se obtiene el siguiente gráfico para \(\displaystyle -\frac{4}{3}x^3+x^2+\frac{1}{2}\) en el intervalo \([-5, 5]\):

Ejemplo: más gráficos polinómicos

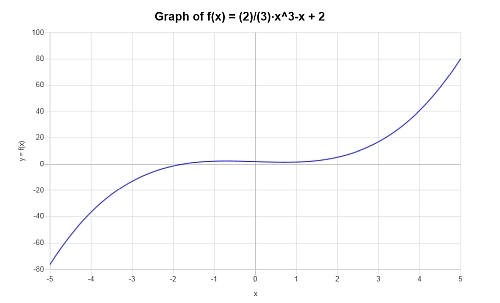
Encuentra la gráfica del siguiente polinomio \( p(x) = \frac{2}{3} x^3 - x +2 \).

Solución: Para este ejemplo, el polinomio provisto es: \(\displaystyle \frac{2}{3} x^3 - x +2 \).

En este caso, la expresión proporcionada es irreducible, por lo que no hay nada que simplificar.

El siguiente gráfico se obtiene para la expresión polinomial dada en el intervalo \([-5, 5]\):

Más calculadoras de polinomios

Graficar polinomios es extremadamente útil ya que nos muestra las principales características de su comportamiento alrededor de sus raíces y su comportamiento final. La representación gráfica generalmente va de la mano con la identificación aproximada de dónde podrían estar las raíces, lo que podría usarse con factorización de polinomios también.

Aunque podemos saber mucho sobre el polinomio con solo graficarlo, todavía necesitamos pasar por el proceso de intentar encontrar raíces racionales , como punto de partida para resolver ecuaciones polinómicas con grado superior a 2 (esto, que no son ecuaciones cuadráticas ).

Adivinar o encontrar sistemáticamente raíces racionales, junto con el uso División larga o División sintética así que para usar el teorema del factor puede conducir a una búsqueda exitosa de raíces polinómicas , pero tal enfoque no siempre funciona, y muchas veces necesita confiar en la calculadora para encontrar aproximaciones numéricas.