Solvers Álgebra

Funciones polinómicas

Instrucciones: Utilice esta calculadora de funciones polinómicas para calcular una operación algebraica que involucre polinomios. Escriba una expresión que involucre alguna operación con polinomios, y la calculadora lo hará, simplificará el resultado y le dará el gráfico, mostrándole todos los pasos.

Funciones polinómicas

Este calculadora de funciones polinómicas te ayudará a calcular funciones de polinomios, calculando y simplificando cualquier expresión polinomial que proporciones.

Puede proporcionar cualquier tipo de expresión que involucre polinomios, y se realizará el cálculo y se tomarán los pasos de simplificación necesarios, para dejar una función polinomial en su forma más compacta. Luego, se proporcionará un gráfico polinomial

Luego, una vez que se haya proporcionado una expresión polinomial válida, puede hacer clic en el botón a continuación, el botón "Calcular", y se mostrarán todos los pasos necesarios del proceso.

El álgebra de fracciones implica la conversión de fracciones, como el uso del denominador común y el uso de reglas aritméticas básicas. Con todo, el proceso de cálculo puede resultar laborioso, aunque se puede realizar de forma sistemática, sin mayor problema.

¿qué es una función polinomial?

Los polinomios, en la explicación más simple, son las funciones que consisten solo en potencias de $x$, posiblemente multiplicadas por constantes numéricas, que se suman (o restan) entre sí. Por ejemplo, $p(x) = x^3 + 2x^2 + 1$ es una función polinomial, ya que consiste en las potencias de $x$ multiplicadas por constantes, sumadas. En este caso, $1 = x^0$ por lo que una constante también es una potencia de $x$. :

En general, una función polinomial tiene la siguiente forma:

\[\displaystyle p(x) = a_0 + a_1 x + a_2 x^2 + .... + a_n x^n \]

con $a_n \ne 0$. En este caso, decimos que el grado del polinomio (o su orden) es $n$, que es la máxima potencia presente en la función polinomial.

Además, el coeficiente $a_n$ se llama Coeficiente de liderazgo , y $a_n x^n$ se llama el término principal . El coeficiente principal y el grado de un polinomio determinarán su comportamiento final (es decir, el comportamiento cuando el valor absoluto de x es grande).

¿cuáles son los pasos para trabajar con una función polinomial?

Paso 1: Identifique claramente la expresión con la que desea trabajar, amplíe y simplifique
Paso 2: Comprueba si los términos que involucran a la variable x solo corresponden a potencias de x, de lo contrario te detienes, no es un polinomio
Paso 3: Asegúrese de que todas las potencias de x se multipliquen por constantes (que podrían ser '1'), y que esos términos aparezcan sumados o restados en la expresión

Es importante asegurarse de tener una función polinomial, de modo que pueda asegurarse de que puede aplicar resultados que son exclusivos de los polinomios, como el teorema del factor el el teorema del resto y el Teorema del cero racional , que son extremadamente útiles para encontrar las soluciones a ecuaciones polinómicas, que son ampliamente utilizadas en diferentes aplicaciones.

Además, la ventaja de trabajar con funciones polinómicas es que puede realizar fácilmente División de polinomios , ya sea usando División larga o División sintética en caso de que el divisor sea lineal.

¿existen funciones polinómicas importantes?

En efecto. Están los notorios polinomios de grado 2, que llamamos polinomios cuadráticos , que se estudian extensamente en Álgebra básica. La razón de esto es que se pueden analizar completamente utilizando fórmulas precisas. Por ejemplo, tienes un fórmula para el vértice , y la famosa fórmula cuadrática se usa para encontrar raíces para polinomios cuadráticos :

\[\displaystyle x = \displaystyle \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

También están los polinomios de grado 2, que llamamos polinomios cúbicos , que también tienen fórmulas explícitas, pero que generalmente se consideran más complejas y, por lo general, no se tratan en los cursos básicos de álgebra.

¿qué sé sobre el comportamiento final de un polinomio?

El comportamiento final de un polinomio dependerá en última instancia del polinomio en sí, pero se pueden decir algunas cosas en función de su grado

Hecho 1: Para polinomios cuadráticos, el gráfico se abre hacia arriba (si el coeficiente principal es positivo) o hacia abajo (si el coeficiente principal es negativo), y la función converge a infinito o menos infinito (según el signo del coeficiente principal) en ambos lados
Hecho 2: Para polinomios con grado impar (por ejemplo, con grado 3) tendrán al menos una raíz real, y la función converge a infinito en un lado, y a menos infinito en el otro lado
Hecho 3: Para polinomios con grado par (por ejemplo, con grado 4), no necesariamente habrá raíces reales (un punto que la gráfica cruza en el eje x), y la función converge a infinito o menos infinito (dependiendo de el signo del coeficiente principal) en ambos lados

Entonces, los polinomios son grandes para valores grandes de x, y si sus valores son positivos o negativos para el positivo de x (en su comportamiento final) depende del signo del coeficiente principal.

Consejos: ¿cuáles son los beneficios de usar una calculadora de funciones polinómicas?

Las calculadoras de polinomios pueden asegurarse de que está llegando a la respuesta correcta. En efecto, cálculos de polinomios no son complicados, pero pueden ser engorrosos y no es difícil cometer errores.

Evite errores algebraicos asegurándose de verificar su trabajo con esta calculadora, para que pueda asegurarse de la consistencia de la respuesta final y los pasos utilizados para llegar allí.

Ejemplo: función polinomial

Calcula la siguiente función polinomial $(x-3)(x-1)(x-4)$

Solución: Se nos proporciona la siguiente expresión polinomial que necesitamos calcular: $\displaystyle (x-3)(x-1)(x-4)$.

Se obtiene el siguiente cálculo:

$ \displaystyle \left(x-3\right)\left(x-1\right)\left(x-4\right)$

Observe that $(x-3) \cdot (x-1) = x^2-1x-3x+3\cdot 1 = x^2-4x+3$, as we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

$ \displaystyle = \,\,$

$\displaystyle \left(x^2-4x+3\right)\left(x-4\right)$

Observe that $(x^2-4x+3) \cdot (x-4) = x^2x-4x^2-4x^2+4\cdot 4x+3x-3\cdot 4 = x^3-8x^2+19x-12$, due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

$ \displaystyle = \,\,$

$\displaystyle x^3-8x^2+19x-12$

lo que concluye el proceso de simplificación de polinomios.

Se obtiene el siguiente gráfico para $\displaystyle x^3-8x^2+19x-12$ en el intervalo $[-5, 5]$:

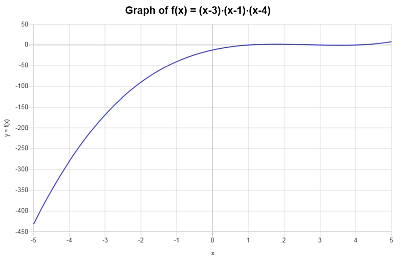
Ejemplo: cálculo de función polinomial

¿Es esta una función polinomial: $\frac{1}{3} x^3+ \frac{5}{4}(x-3)(x - \frac{5}{6})$

Solución:

Se nos proporciona la siguiente expresión polinomial que necesitamos calcular: $\displaystyle \frac{1}{3} x^3+ \frac{5}{4}(x-3)(x - \frac{5}{6})$.

Se obtiene el siguiente cálculo:

$ \displaystyle \frac{1}{3}x^3+\frac{5}{4}\left(x-3\right)\left(x-\frac{5}{6}\right)$

We get that $(x-3) \cdot (x-\frac{5}{6}) = x^2-\frac{5}{6}x-3x+3\cdot \frac{5}{6} = x^2-\frac{23}{6}x+\frac{5}{2}$, as we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

$ \displaystyle = \,\,$

$\displaystyle \frac{1}{3}x^3+\frac{5}{4}\left(x^2-\frac{23}{6}x+\frac{5}{2}\right)$

We get that $(\frac{5}{4}) \cdot (x^2-\frac{23}{6}x+\frac{5}{2}) = \frac{5}{4}x^2-\frac{5}{4}\cdot \frac{23}{6}x+\frac{5}{2}\cdot \frac{5}{4} = \frac{5}{4}x^2-\frac{115}{24}x+\frac{25}{8}$, by using the distributive property on each term of the expression on the left, with respect to the terms on the right

$ \displaystyle = \,\,$

$\displaystyle \frac{1}{3}x^3+\frac{5}{4}x^2-\frac{115}{24}x+\frac{25}{8}$

que finaliza el proceso de simplificación.

Gráficamente se obtiene lo siguiente para la función simplificada $\displaystyle \frac{1}{3}x^3+\frac{5}{4}x^2-\frac{115}{24}x+\frac{25}{8}$ en el intervalo $[-5, 5]$:

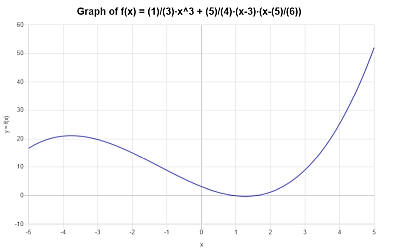
Ejemplo: usar una calculadora de polinomios

Calcula $ x^2 - (2x - 1)x $.

Solución: En este ejemplo final tenemos $\displaystyle x^2 - (2x - 1)x $, que necesitamos simplificar.

Se obtiene el siguiente cálculo:

$ \displaystyle x^2-\left(2x-1\right)x$

Notice that $(2x-1) \cdot (x) = 2x^2-1x = 2x^2-x$, due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

$ \displaystyle = \,\,$

$\displaystyle x^2-2x^2+x$

Putting together the terms with $x^2$

$ \displaystyle = \,\,$

$\displaystyle x+\left(1-2\right)x^2$

Operating the terms that were grouped with $x^2$

$ \displaystyle = \,\,$

$\displaystyle x-x^2$

lo que pone fin a la simplificación.

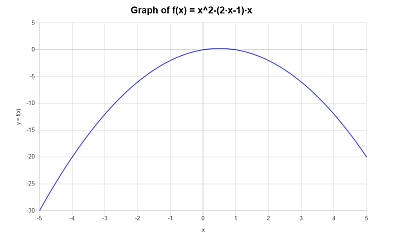
Se obtiene el siguiente gráfico para $\displaystyle -x^2+x$ en el intervalo $[-5, 5]$:

Más calculadoras de álgebra

Las funciones polinómicas son literalmente la pieza central en Álgebra. Para aplicaciones básicas, polinomios cuadráticos Tendrán un papel fundamental la Economía, la Física y la Ingeniería.

Las funciones polinómicas tienen propiedades extremadamente poderosas, especialmente relacionadas con el cálculo de raíces polinómicas , que tienen un fuerte significado en las aplicaciones.