Más información sobre esta calculadora de grados a radianes

¿Por qué tenemos ángulos medidos en grados y ángulos medidos en radianes? La respuesta es simple: porque diferentes sistemas de medición de ángulos usan diferentes referencias para denominar la medida del círculo completo.

Diferentes referencias para el círculo completo

Cuando medimos un ángulo en grados, la apertura completa de un círculo corresponderá a un ángulo de 360 ^o . Luego, los ángulos se calculan proporcionalmente a esas referencias. Es decir, un ángulo correspondiente a la apertura del círculo completo será la mitad de lo que corresponde a la apertura completa, esto es la mitad de 360 ^o , que es 180 ^o

Ahora, si medimos un ángulo en radianes el ángulo correspondiente a la apertura total del círculo se establece como el perímetro de un círculo de radio 1, esto es \(2\pi\). En otras palabras, está midiendo un ángulo en términos de cuántos radios deben usarse para describir la abertura. De esta manera, un 360 ^o el ángulo corresponde a \(2\pi\) radianes.

¿Cómo convertir grados a radianes?

Ahora, si realmente quieres ir y transformar un ángulo en grados a radianes, ¿qué haces? Esto es lo que debe hacer: si tiene un ángulo \(d\) medido en grados y desea convertirlo en un ángulo equivalente n \(r\) que se mide en radianes, utilice la siguiente fórmula:

\[r = \frac{\pi d}{180} \]

La fórmula anterior se aplica ya sea que convierta decimales o fracciones de grados a radianes. Todo lo que necesita hacer es introducir el número de grados \(d\) en la fórmula

Ejemplo 1: Convertir 45 ^o en radianes.

Solución: Todo lo que necesita hacer es conectar \(d\) en la fórmula anterior. En este caso, \(d = 45^o\), entonces obtenemos

\[r = \frac{\pi d}{180} \pi \frac{ 45}{180} = \frac{\pi}{4} \] so then 180 ^o degrees corresponds to \(\frac{\pi}{4}\) radians.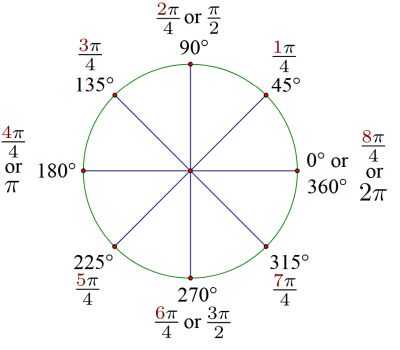

Usando Excel para la conversión de ángulos

Para aquellos de ustedes que trabajan con Excel, pueden usar la función "= RADIANES (d)" para convertir un ángulo d en grados a radianes.

Si, por el contrario, puede utilizar esta otra calculadora para convertir radianes a grados , que esencialmente aplica la fórmula anterior pero resuelve \(r\).

Puede explorar otras calculadoras trigonométricas, como nuestra calculadora de doble ángulo , Entre muchos otros.