El concepto de función es extremadamente importante y está absolutamente omnipresente en matemáticas. Es por eso que debemos darle un buen repaso, antes de intentar comprender algunas de las ventajas que vendrán después cuando profundicemos en los temas de cálculo, como la diferenciación y la integración.

¿QUÉ ES UN SET?

El primer elemento que debemos comprender es el concepto de conjunto . Un conjunto es simplemente una colección de elementos. Entonces, un conjunto se define de manera bastante simple mediante el conocimiento de qué elementos pertenecen al conjunto y qué elemento no. Parece ser una tarea súper simple y la teoría de conjuntos debería reducirse simplemente a tener reglas inequívocas para determinar qué elementos pertenecen a un conjunto.

Por ejemplo, definamos el conjunto de números pares y lo llamamos \(E\). ¿Por qué es incluso un conjunto? Porque tiene una regla inequívoca para determinar qué elementos pertenecen a \(E\): Un número real \(x\) pertenece a \(E\) si es divisible por 2. La regla funciona sin ambigüedades para cada número real individual determinando si pertenece o no a \(E\). Por qué digo “sin ambigüedades” y sigo repitiendo. Porque es importante. Sin ambigüedades significa que no hay forma de concluir que un \(x\) dado pertenece y no pertenece a \(E\). Lamentablemente, las cosas a veces van más allá de nuestra imaginación. Contrariamente a nuestra intuición, un conjunto definible con una simple regla de pertenencia puede conducir a una clasificación de pertenencia ambigua (contradictoria), como lo muestra Bertrand Russell en su famosa paradoja. Russell demostró que debería usarse una definición más cuidadosa de lo que es un conjunto.

Para todos los propósitos prácticos, pensaremos en un conjunto como una colección de elementos, definible por una regla de pertenencia. .

¿CUÁL ES EL PRODUCTO DE DOS JUEGOS?

Deje que \(A\) y \(B\) sean conjuntos, en el contexto de la definición dada anteriormente. El producto \(A\times B\) de dos conjuntos es otro conjunto, que se define como el conjunto de todos los pares ordenados posibles de la forma \(\left( a, b \right)\), donde \(a\) pertenece a \(A\) y \(b\) pertenece a \(B\). Entonces, \(A\times B\) es un conjunto, y sus elementos son pares ordenados de la forma \(\left( a ,b \right)\). No dejes que esa notación te impresione. Cuando digo "pares ordenados de la forma \(\left( a, b \right)\)", el símbolo \(\left( a, b \right)\) es un símbolo inventado, para indicar un elemento que se compone de dos entidades \(a\) y \(b\), e identifico el primer elemento como \(a\), y el segundo elemento como \(b\) . Eso es. En lugar de \(\left( a,b \right)\), podríamos haber elegido el símbolo \(a\_b\), y habría funcionado bien.

Tendrás que perdonarme, pero tengo que escribir la definición matemática del producto de dos conjuntos (también podemos multiplicar conjuntos ... ¿qué pensaste, nos quedaríamos solo con números, eh?):

\(A\times B=\left\{ \left( a,b \right):\,\,\,a\in A,\,\,\,b\in B \right\}\)

La razón por la que escribo la definición es para que la mire y reconozca cómo, usando una notación muy compacta, estamos diciendo exactamente lo mismo que la forma en que la definí con palabras en el párrafo anterior. Espero que afloje un poco el miedo a leer enunciados matemáticos. Los matemáticos a veces pueden ser personas extravagantes, pero encuentran notaciones buenas, inequívocas y compactas. Y en consecuencia, el lenguaje matemático es SUPER fácil de leer. ¿Correcto? ¿Correcto? Por favor dime que tengo razón ...

Una nota al margen, por razones históricas, el producto de dos conjuntos \(A\times B\) normalmente se denomina producto cartesiano .

AHORA, LA DEFINICIÓN DE UNA FUNCIÓN (FINALMENTE)

Ok, mentí, hay un paso más antes de definir qué es una función. Necesitamos definir el concepto de relación . ¿Qué es una relación? Más allá de su uso común como palabra en inglés, una relación es simplemente un subconjunto de un producto cartesiano. CUALQUIER subconjunto de un producto cartesiano es una relación. Entonces, si \(A\) y \(B\) son conjuntos, un conjunto \(R\) es una relación si \(R\subseteq A\times B\). Dado que cualquier conjunto puede considerarse un subconjunto de sí mismo, todos los productos cartesianos son relaciones en sí mismos.

Ponlo en un marco:

Una relación es un conjunto que es un subconjunto de un producto cartesiano

Seamos más gráficos. Considere el conjunto \(A=\left[ 0,1 \right]\) (que son todos los números reales que son mayores o iguales que 0, y también son menores o iguales que 1). ¿Qué es el producto cartesiano \(A\times A\)? Repitamos lo que acabamos de aprender. El producto cartesiano \(A\times A\) es \(\left[ 0,1 \right]\times \left[ 0,1 \right]\) en este caso es el conjunto de todos los pares\(\left( x, y \right)\), donde tanto \(x\) como \(y\) pertenecen a \(\left[ 0,1 \right]\). Los productos cartesianos suelen ser fáciles de graficar. Mire la región sombreada a continuación:

Ahora bien, ¿qué haría una relación? Podemos "tallar" todo lo que queramos en la región sombreada de arriba, y lo que queda es una relación en \(\left[ 0,1 \right]\times \left[ 0,1 \right]\). Por ejemplo, podemos cortar las "esquinas" para obtener la siguiente subregión:

La región (conjunto) anterior es una relación. ¿Por qué? Porque es un subconjunto del producto cartesiano \(\left[ 0,1 \right]\times \left[ 0,1 \right]\). Pero podemos sacar aún más. ¿Qué tal tallar un cuarto de círculo? Vea la región a continuación.

La región (conjunto) anterior es una relación. ¿Por qué? Nuevamente, porque es un subconjunto del producto cartesiano \(\left[ 0,1 \right]\times \left[ 0,1 \right]\).

Ahora, déjeme darle un ejemplo de dos relaciones en \(\left[ -1,1 \right]\times \left[ -1,1 \right]\). Vea los gráficos a continuación:

Relación 1

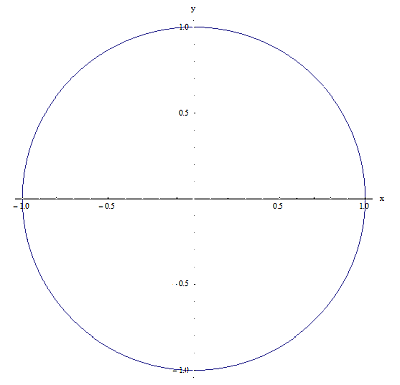
Relación 2

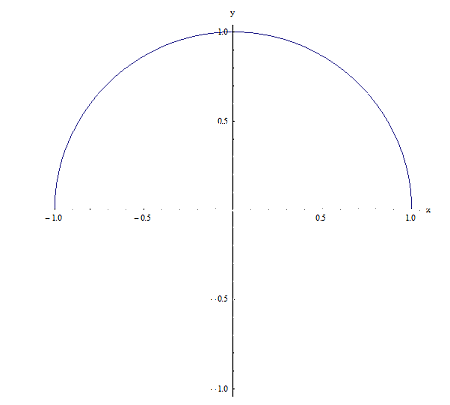
Ambos son obviamente relaciones (porque ambos están contenidos en el producto cartesiano \(\left[ -1,1 \right]\times \left[ -1,1 \right]\), pero tienen una diferencia clave: para la relación 1, para un punto x dado en \(\left[ -1,1 \right]\), hay dos puntos \({{y}_{1}}\) y \({{y}_{2}}\) que tienen la propiedad de que \(\left( x,{{y}_{1}} \right)\) y __XYZ_F a la relación 1. Por ejemplo, para x = 0, hay dos puntos \({{y}_{1}}=1\) y \({{y}_{2}}=-1\) de modo que \(\left( 0,1 \right)\) y\(\left( 0,-1 \right)\) pertenecen a la relación 1. Ahora, para la relación 2 ese no es el caso porque, por ejemplo, para x = 0 es sólo \(y=1\) que hace que el punto \(\left( 0,1 \right)\) pertenezca a la relación 1.

Finalmente podemos definir una función: Una función \(R\) es un conjunto que es una relación y también tiene la propiedad de que si el punto \(\left( x,y \right)\) pertenece a \(R\), entonces no hay otro punto \(\bar{y}\) diferente de \(y\) que tenga la propiedad de que \(\left( x,\bar{y} \right)\)__A__XYZ_ también. En otras palabras, una función es una relación con el requisito adicional de que cada \(x\) en su dominio está asociado con solo un \(y\).

¿Cómo saber diferenciar entre una función y una relación?

¡Artilugio! Usamos un pequeño truco llamado "Prueba de la línea vertical": dibujamos una línea vertical imaginaria y la barremos moviéndola de izquierda a derecha hasta el final y haciendo un mapa mental de dónde la línea vertical se cruza con la relación.

• Si en CUALQUIER punto, la línea vertical interseca la relación en MÁS de un punto, entonces la relación no pasa la prueba de la línea vertical, y entonces la relación no es una función

• Si en CUALQUIER punto, la línea vertical no interseca la relación en ningún lugar en MÁS de un punto, entonces la relación pasa la prueba de la línea vertical, y entonces la relación es una función

Vea los dos ejemplos a continuación:

Ejemplo 1: No pasa la prueba de la línea vertical porque la línea vertical que se muestra en la figura interseca la relación en más de un punto: NO ES UNA FUNCIÓN

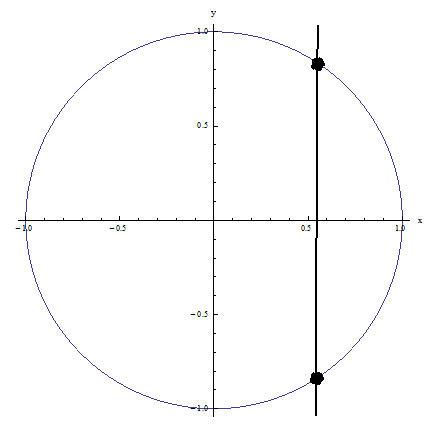
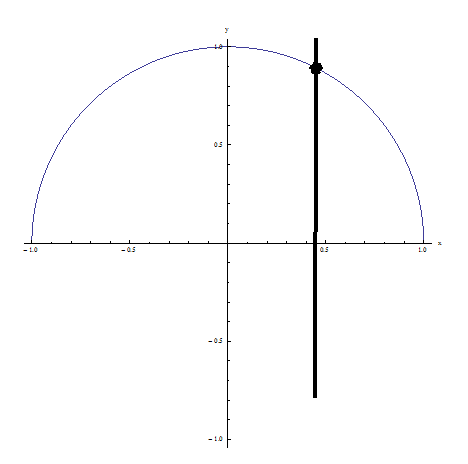
Ejemplo 2: Pasa la prueba de la línea vertical porque ninguna línea vertical cruza la relación en más de un punto: ¡ES UNA FUNCIÓN!

Hay muchas aplicaciones gráficas que se pueden realizar con funciones, incluido el cálculo de asíntotas horizontales , asíntotas verticales y asíntotas inclinadas si corresponde.