¿cómo usar este creador de diagramas de dispersión?

Más sobre diagramas de dispersión : Los diagramas de dispersión son dispositivos gráficos bivariados. El término "bivariado" significa que se construye para analizar el tipo de asociación entre dos variables de intervalo \(X\) y \(Y\). Los datos deben venir en forma de pares ordenados \((X_i, Y_i)\), y esos pares se representan en un conjunto de ejes cartesianos.

Normalmente, se utiliza un diagrama de dispersión para evaluar si las variables \(X\) y \(Y\) tienen o no una asociación lineal, pero podría haber otros tipos de asociaciones no lineales (cuadráticas, exponenciales, etc.). La existencia de una asociación lineal se evalúa estableciendo qué tan apretados están los datos alrededor de una línea recta.

Los pares de datos \((X_i, Y_i)\) que están poco agrupados alrededor de una línea recta tienen una asociación lineal débil o inexistente, mientras que los pares de datos \((X_i, Y_i)\) que están muy agrupados alrededor de una línea recta tienen una fuerte asociación lineal. Ser capaz de evaluar rápidamente la asociación lineal entre dos variables es uno de los propósitos principales de usar un generador de diagramas de dispersión.

Una forma numérica (cuantitativa) de evaluar el grado de asociación lineal para un conjunto de pares de datos es calculando el coeficiente de correlación .

¿cómo se hace un diagrama de dispersión?

Los estudiantes a menudo se preguntan cómo pueden trazar un diagrama de dispersión. Por lo general, un diagrama de dispersión se hará utilizando algún tipo de software computacional, como Excel. Por lo general, los estilos y los esquemas de color pueden cambiar un poco, pero en términos generales, el diagrama de dispersión que puede hacer con este gráfico se parece mucho a los proporcionados por Excel o cualquier otro paquete de software diferente.

Si vas a hacer un diagrama de dispersión a mano, entonces las cosas son un poco más elaboradas: necesitas lidiar con los ejes x e y correspondientes, y sus escalas correspondientes. Luego, es necesario identificar cada par \((X, Y)\), y ubicarlo en el plano, respetando la escala correspondiente definida para cada uno de los ejes.

¿cómo puedes describir la correlación de un diagrama de dispersión?

Se utiliza un diagrama de dispersión para evaluar el grado de asociación lineal entre dos variables. Cuanto más fuerte sea el grado de asociación lineal que vemos, más cercano será el valor absoluto de la correlación será a 1.

En términos generales, mirando el diagrama de dispersión podemos estimar la fuerza de la asociación lineal entre las dos variables, pero para obtener una magnitud precisa, necesitamos calcular el valor numérico del coeficiente de correlación correspondiente.

Por ejemplo, el diagrama de dispersión a continuación muestra un grado débil de asociación lineal positiva, por lo que uno esperaría que el coeficiente de correlación sea positivo pero cercano a cero.

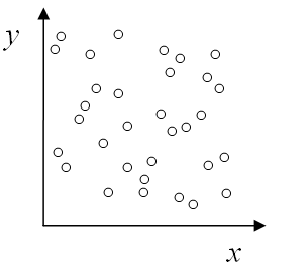
Por otro lado, en el diagrama de dispersión a continuación tenemos un grado moderadamente fuerte de asociación lineal positiva, por lo que uno esperaría que el coeficiente de correlación sea positivo, relativamente cercano a 1 pero no demasiado cercano.

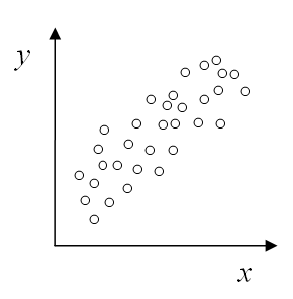
Finalmente, en el siguiente diagrama de dispersión tenemos un fuerte grado de asociación lineal positiva, por lo que uno esperaría que el coeficiente de correlación sea positivo y cercano a 1.

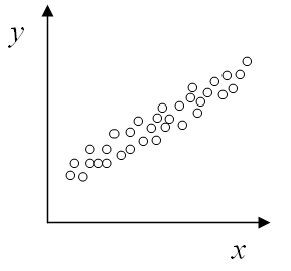
El vínculo entre la correlación y la regresión lineal

Cuando dos variables X e Y exhiben un grado significativo de asociación lineal, entonces tiene sentido estimar un modelo de regresión lineal , con el fin de predecir una variable en términos de la otra.

Para estimar un modelo de la forma Y = a + b X + e, a calculadoras de mínimos cuadrados tendrá que ser utilizado. Este enfoque consiste en encontrar los parámetros de una línea que minimice la suma de los errores al cuadrado.

¿qué otros creadores de gráficos puedo usar?

Otros creadores de gráficos que están disponibles en nuestro sitio son nuestros Creador de diagramas de Pareto , creador de gráficos circulares , gráfico de ojiva y Creador de gráficos de barras , Por mencionar sólo algunos.