Calculadora de división larga de polinomios

Esta calculadora te ayuda con el proceso de realizar una división larga entre dos polinomios dados. Para ello, debe proporcionar dos expresiones polinómicas válidas. Estos polinomios pueden estar ya simplificados o no, y la calculadora los simplificará si lo necesitan.

Cuándo dividir polinomios debe proporcionar dos polinomios, uno por el que dividirá, que se llama dividendo, y el otro es el divisor.

Una vez que proporcione dos válidos polinomios , el siguiente paso sería hacer clic en el botón "Calcular", que mostrará todos los cálculos correspondientes necesarios para la división larga deseada entre los polinomios proporcionados.

El proceso de realizar una división de polinomios usando el Método De División Larga es un método relativamente sencillo, pero que requiere un enfoque muy organizado, para no perderse. Por lo general, funciona mejor con un enfoque tabular para mostrar los pasos correspondientes.

Se utiliza un enfoque más simple con División sintética , pero eso solo se aplica cuando el divisor tiene grado uno, por lo que tiene un alcance más limitado

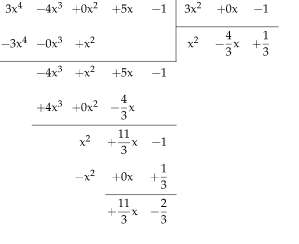
¿qué es un polinomio?

Un polinomio es un tipo de expresión simple que combina con sumas y restas las potencias enteras de una cierta variable x (o cualquier nombre de variable que se elija), posiblemente multiplicada por constantes.

Por ejemplo, la expresión \(p(x) = 2x^2 + x + 1\) es una combinación de los términos \(2x^2\), \(x\) y \(1\) con sumas de potencias de x (nótese que 1 es una potencia de x, como \(x^0 = 1\).

Por otro lado, \(f(x) = 2x^2 + \sin(x) + 1\) no es un polinomio, porque el término \(\sin(x)\) no es potencia de x.

Operaciones con polinomios

Los polinomios, al igual que los números, se pueden operar con sumas, restas, multiplicaciones y divisiones de polinomios . Las sumas y restas son simples de hacer, de una manera muy intuitiva. Por ejemplo, si tiene dos polinomios, \(p(x) = 2x+1\) y \(q(x) = x^3 + 2x+ 3\), la suma del polinomio se logra sumando literalmente los términos como

\[p(x) + q(x) = 2x + 1 + x^3 + 2x+ 3 = x^3 + 4x + 4\]

Para las restas, también resta los términos correspondientes del polinomio que se está restando. Por ejemplo, si tiene dos polinomios, \(p(x) = 2x+1\) y \(q(x) = x^3 + 2x+ 3\), entonces, la resta se realiza como

\[p(x) - q(x) = 2x + 1 - (x^3 + 2x+ 3) = 2x + 1 - x^3 - 2x - 3) = -x^3 -2\]

La multiplicación es más complicada, porque tienes que cruzar términos usando la propiedad distributiva:

\[p(x) \cdot q(x) = (2x + 1) \cdot (x^3 + 2x+ 3) = 2x \cdot x^3 + 2x \cdot 2x + 2x \cdot 3 + 1\cdot x^3 + 1\cdot1 2x+ 1\cdot 3 = 2x^4 +x^3+4x^2+8x+3\]

La división es un poco más complicada, porque involucra la idea de que un polinomio no puede dividir exactamente otro polinomio. Matemáticamente, cuando tenemos dos polinomios \(p(x)\) y \(s(x)\), y queremos dividir \(p(x)\) entre \(s(x)\), buscamos un cociente \(q(x)\) y un resto \(r(x)\) (ambos polinomios), que tienen la propiedad de que \(p(x)= q(x)\cdot s(x) + r(x)\), con la condición de que el grado del polinomio \(r(x)\) es menor que el grado de \(s(x)\). Esto generalmente se llama el Descomposición De Euclides .

El método de división larga

Entonces, el método de división larga es una forma sistemática de comenzar con dos polinomios que queremos dividir \(p(x)\) y \(s(x)\), por lo que encontramos el cociente \(q(x)\) y un resto \(r(x)\) en tales una manera que

\[p(x)= q(x)\cdot s(x) + r(x)\]

Este algoritmo es extremadamente útil, y aunque el problema parece simple en apariencia, no es difícil perderse si no se usa un enfoque sistemático, que garantice llegar al cociente y al resto requeridos.

¿cuáles son los pasos para hacer una división larga?

• Paso 1: Identifique los dos polinomios p(x) y s(x) que desea dividir e identifique p(x) como el dividendo y s(x) como el divisor
• Paso 2: Compara el grado del dividendo p(x) con el grado de s(x). Si el grado de s(x) es mayor que el grado de p(x), tenemos que el resto es el mismo dividendo p(x), y el cociente es cero: q(x) = 0, y listo
• Paso 3: En este caso, asumimos que el grado del dividendo p(x) es mayor o igual que el grado de la división s(x), de lo contrario, nos habríamos detenido en el paso 2
• Paso 4: Necesitamos llevar a cabo un proceso iterativo para encontrar un resto temporal, hasta que hayamos llegado a un resto que tenga un grado menor que el grado de s(x)
• Paso 5: El resto temporal o intermedio se actualiza cada vez encontrando primero la relación entre el término más alto del resto temporal actual y el divisor s(x). Esta relación (que es un término de potencia) se multiplica luego por s(x), y el resultado de esta multiplicación se resta del resto temporal actual, lo que genera un resto actualizado.
• Paso 6: Este proceso continúa hasta que el resto tiene un grado inferior al de s(x). En cada paso de la iteración, el grado del resto temporal se reduce en al menos 1, por lo que se garantiza que el proceso finaliza

Al final, el proceso de dividir dos polinomios se reduce a calcular multiplicaciones que son sumas de polinomios, que es más o menos lo que sucede con los números. El método de división larga para polinomios es la extensión de la forma en que dividimos números en polinomios.

¿cómo se conecta la división larga con la búsqueda de raíces de una ecuación polinomial?

Suponga que p(x) es el dividendo que desea dividir y s(x) es el divisor. De acuerdo con el método de la División Larga, podrás encontrar un cociente q(x) y un resto r(x) tal que:

\[\displaystyle p(x) = q(x)s(x) + r(x) \]

Pero a veces sucede que el resto es r(x) = 0, y en ese caso decimos que s(x) divide a p(x) (o divide exactamente a p(x)). Entonces, cuando r(x) = 0

\[\displaystyle p(x) = q(x)s(x) \]

Esto indica que para encontrar raíces de p(x) = 0, podemos resolver q(x) = 0 y s(x) = 0, por separado, que son ecuaciones más sencillas de resolver.

Ventajas de esta calculadora de división larga

Como mencioné antes, la división larga no es demasiado difícil, pero requiere un enfoque sistemático. Una gran ventaja de usar un calculadora de división como este es que obtendrá todos los pasos del proceso que se muestran

Puede que no sea esencial saber cómo realizar los pasos usted mismo, pero esta calculadora le permite ver cómo se hace, explicando cada paso, eliminando el misterio de obtener el resto y el cociente de, digamos, una calculadora digital, que le dará usted la respuesta sin mostrar los pasos.

Una calculadora de división larga con pasos que muestran todo el trabajo asegura que tenga una idea clara de lo que está sucediendo con el cálculo.

Ejemplo: cálculo de la división de polinomios

Calcula la división de los siguientes polinomios: \(p(x) = \frac{1}{3} x^3 + \frac{5}{4}x - \frac{5}{6}\) y \(s(x) = x+3\).

Solución: Se ha proporcionado el siguiente polinomio: \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\), que debe dividirse por el polinomio \(\displaystyle s(x) = x+3\).

Observe que el grado del dividendo es \(\displaystyle deg(p) = 3\), mientras que el grado del divisor es \(\displaystyle deg(s)) = 1\).

Paso 1: El término principal del dividendo \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\) es \(\displaystyle \frac{1}{3}x^3\), mientras que el término principal del divisor \(\displaystyle s(x) = x+3\) es igual a \(\displaystyle x\).

Entonces, el término que necesitamos multiplicar \(x\) para llegar al término principal del dividendo es \(\displaystyle \frac{ \frac{1}{3}x^3}{ x} = \frac{1}{3}x^2\), entonces sumamos este término al cociente. Además, multiplicamos esto por el divisor para obtener \(\displaystyle \frac{1}{3}x^2 \cdot \left(x+3\right) = \frac{1}{3}x^3+x^2\), que debemos restar al dividendo:

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle & \displaystyle &\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \end{array}\]

Paso 2: En este caso, el término principal del resto actual \(\displaystyle -x^2+\frac{5}{4}x-\frac{5}{6}\) es \(\displaystyle -1x^2\), y sabemos que el término principal del divisor es \(\displaystyle x\).

Entonces, el término que necesitamos multiplicar \(x\) para llegar al término principal del resto actual es \(\displaystyle \frac{ -1x^2}{ x} = -x\), entonces sumamos este término al cociente. Además, multiplicamos esto por el divisor para obtener \(\displaystyle -x \cdot \left(x+3\right) = -x^2-3x\), que debemos restar al recordatorio actual:

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle -x & \displaystyle &\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle +3x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle \frac{17}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \end{array}\]

Paso 3: En este caso, el término principal del resto actual \(\displaystyle \frac{17}{4}x-\frac{5}{6}\) es \(\displaystyle \frac{17}{4}x\), y sabemos que el término principal del divisor es \(\displaystyle x\).

Entonces, el término que necesitamos multiplicar \(x\) para llegar al término principal del resto actual es \(\displaystyle \frac{ \frac{17}{4}x}{ x} = \frac{17}{4}\), entonces sumamos este término al cociente. Además, multiplicamos esto por el divisor para obtener \(\displaystyle \frac{17}{4} \cdot \left(x+3\right) = \frac{17}{4}x+\frac{51}{4}\), que debemos restar al recordatorio actual:

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle -x & \displaystyle +\frac{17}{4}&\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle +3x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle \frac{17}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle & \displaystyle -\frac{17}{4}x & \displaystyle -\frac{51}{4}\\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle & \displaystyle -\frac{163}{12}\\[0.8em] \end{array}\]

con lo cual concluye este cálculo, ya que el grado del resto actual \(r(x) = -\frac{163}{12}\) es menor que el grado del divisor \(s(x) = x+3\).

Conclusión: Therefore, we conclude that for the given dividend \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\) and divisor \(\displaystyle s(x) = x+3\), we get that the quotient is \(\displaystyle q(x) = \frac{1}{3}x^2-x+\frac{17}{4}\) and the remainder is \(\displaystyle r(x) = -\frac{163}{12}\), and that