Más sobre la gráfica de probabilidad normal

Un gráfico de probabilidad normal es un gráfico que normalmente se utiliza para evaluar la normalidad de la distribución a la que pertenecen los datos de muestra pasados.

Existen diferentes tipos de gráficos de normalidad (PP, QQ y otras variedades), pero todos se basan en la misma idea: los cuantiles teóricos de una distribución normal estándar se grafican en función de los cuantiles observados.

Por lo tanto, si los datos de muestra provienen de una población distribuida con normalidad , entonces el gráfico de probabilidad normal debería verse como un 45 ^oh Línea, con variaciones aleatorias. Si no es así, y el patrón del gráfico de probabilidad normal se desvía significativamente/sistemáticamente del gráfico de probabilidad normal, se debe sospechar que la distribución no es normal.

¿cómo se calcula un gráfico de probabilidad normal?

Hay varios pasos concretos que debes seguir, en un orden específico, para construir un gráfico de probabilidad normal

1. En este caso concreto, los datos se ordenan en orden ascendente y los llamamos \(X_1, X_2, ...., X_i , ...., X_n\).
2. Para cada \(X_i\) en esta secuencia de datos ordenados, calculamos las frecuencias teóricas \(f_i\), que se aproximan utilizando la siguiente fórmula:
\[ f_i = \frac{i - 0.375}{n + 0.25} \] (where \(i\) corresponds to the position in the ordered dataset)
3. Luego calculamos también \(z_i\), cuyo puntaje z asociado corresponde como
\[ z_i = \Phi^{-1}(f_i)\]
4. Luego, el gráfico de probabilidad normal se obtiene trazando los valores X ordenados (sus datos de muestra) en el eje horizontal y los valores \(z_i\) correspondientes en el eje vertical.

Gráfico de probabilidad normal de excel

Puedes trazar un gráfico de probabilidad normal en Excel, pero lleva algo de tiempo

Calculadoras para la distribución normal y otras

Otros creadores de gráficos que puedes utilizar son nuestros graficador de distribución normal , Creador de diagramas de dispersión o nuestro Creador de diagramas de Pareto .

Ejemplo: cálculo de un gráfico de probabilidad normal

Pregunta :Se le proporcionan los siguientes datos de muestra: 2, 3, 4, 3, 3, 2, 3, 4, 5, 3, 2, 3, 1, 2, 3, 4, 5, 6, 3, 2, 4, 5, 6 10 10 10 12 12 1 2 3 3 y 23. Construya un gráfico de probabilidad normal.

Solución:

Necesitamos construir un gráfico de probabilidad normal. Estos son los datos de muestra proporcionados:

Observación:	\(X\)
1	2
2	3
3	4
4	3
5	3
6	2
7	3
8	4
9	5
10	3
11	2
12	3
13	1
14	2
15	3
16	4
17	5
18	6
19	3
20	2
21	4
22	5
23	6
24	10
25	10
26	10
27	12
28	12
29	1
30	2
31	3
32	3
33	23

Es necesario calcular las frecuencias teóricas \(f_i\) así como los puntajes z asociados \(z_i\), para \(i = 1, 2, ..., 33\):

Observe que las frecuencias teóricas \(f_i\) se aproximan utilizando la siguiente fórmula:

\[ f_i = \frac{i - 0.375}{n + 0.25} \]

donde \(i\) corresponde a la posición en el conjunto de datos ordenado y \(z_i\) es la puntuación z asociada correspondiente. Esto se calcula como

\[ z_i = \Phi^{-1}(f_i)\]

Se obtiene la siguiente tabla

Posición (i)	X (Orden Ascendente)	F i	z i
1	1	0.0188	-2.079
2	1	0.0489	-1.656
3	2	0.0789	-1.412
4	2	0.109	-1.232
5	2	0.1391	-1.084
6	2	0.1692	-0.957
7	2	0.1992	-0.844
8	2	0.2293	-0.741
9	3	0.2594	-0.645
10	3	0.2895	-0.555
11	3	0.3195	-0.469
12	3	0.3496	-0.386
13	3	0.3797	-0.306
14	3	0.4098	-0.228
15	3	0.4398	-0.151
16	3	0.4699	-0.075
17	3	0.5	0
18	3	0.5301	0.075
19	4	0.5602	0.151
20	4	0.5902	0.228
21	4	0.6203	0.306
22	4	0.6504	0.386
23	5	0.6805	0.469
24	5	0.7105	0.555
25	5	0.7406	0.645
26	6	0.7707	0.741
27	6	0.8008	0.844
28	10	0.8308	0.957
29	10	0.8609	1.084
30	10	0.891	1.232
31	12	0.9211	1.412
32	12	0.9511	1.656
33	23	0.9812	2.079

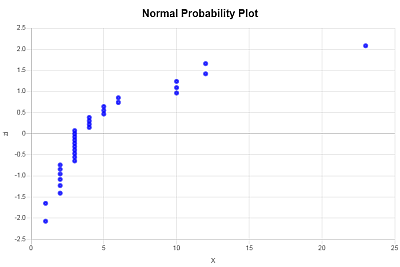
El gráfico de probabilidad normal se obtiene trazando los valores X (datos de muestra) en el eje horizontal y los valores \(z_i\) correspondientes en el eje vertical. Se obtiene el siguiente gráfico de normalidad: