Más acerca de esta herramienta de cálculo de probabilidad de distribución normal

Aquí hay algunos datos sobre el probabilidad de distribución normal para que puedas entender mejor este generador de gráficos de distribución normal. En primer lugar, la probabilidad normal es un tipo de distribución de probabilidad continua que puede tomar valores aleatorios en toda la línea real. Las principales propiedades de la distribución normal son:

• Es continuo (y como consecuencia, la probabilidad de obtener un resultado único y específico es cero)


• Tiene una distribución "en forma de campana" (y de ahí viene el nombre "Bell-Curve")


• La distribución normal está determinada por dos parámetros: la media de la población y la desviación estándar de la población.


• es simétrica con respecto a su media

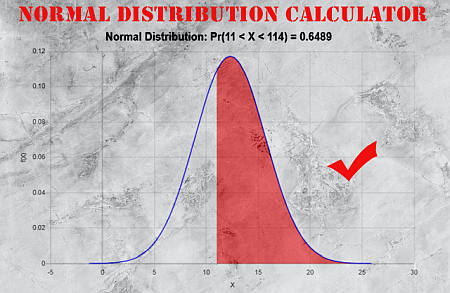
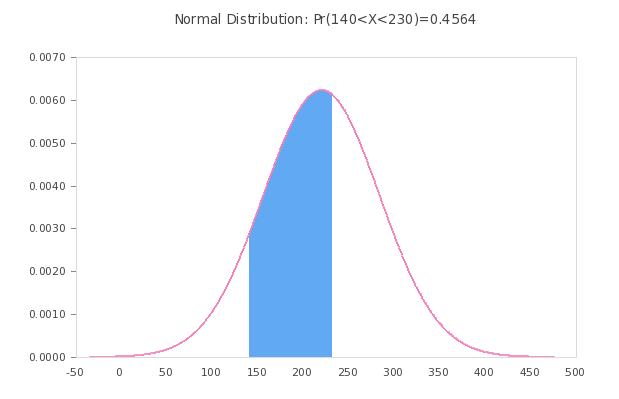
Utilizando lo anterior calculadora de curva de distribucion normal , podemos calcular probabilidades de la forma \(\Pr(a \le X \le b)\), junto con su respectivo gráficos de distribución normal . Esto no es exactamente un calculadora de densidad de probabilidad normal , pero es una calculadora de distribución normal (acumulativa). Cambie los parámetros para a y b para graficar la distribución normal según sus necesidades de cálculo. Si necesita calcular \(\Pr(3 \le X \le 4)\), escribirá "3" y "4" en los cuadros correspondientes del script.

Un caso especial muy importante consiste en el caso del Distribución normal estándar , que corresponde al caso de una distribución normal con media igual a \(\mu = 0\), y desviación estándar igual a \(\sigma = 1\). En los casos de una distribución normal regular o de una distribución normal estándar, todos pueden manejarse con la calculadora de probabilidad anterior.

Parámetros de la distribución normal

Por lo tanto, no olvide que la distribución normal en general está determinada por su media y su desviación estándar. La media puede ser cualquier número real y la desviación estándar puede ser cualquier número no negativo.

Pero en particular, la distribución normal estándar es una distribución normal que tiene la propiedad de que la media de la distribución normal estándar es cero y la desviación estándar de la distribución normal estándar es 1.

No dude en contactarnos si tiene alguna pregunta sobre este generador de gráficos de distribución normal.

Enlace con la distribución normal y la cdf normal

La cdf normal es la abreviatura de la función de distribución acumulativa normal, que para un valor dado de \(z\), proporciona la probabilidad total hasta el valor del valor dado \(z\).

Puedes usar esto calculadora cdf normal para calcular la probabilidad acumulada que desee, y es lo mismo que usar esta calculadora de distribución normal con límite inferior \(-\infty\) y límite superior \(z\).

La distribución normal y las puntuaciones z

En muchos aspectos, puede ver una calculadora de distribución normal como una calculadora de probabilidad de puntuación z , debido a la forma en que calculamos las probabilidades normales en general.

De hecho, cuando tiene una distribución normal general con la media \(\mu\) y \(\sigma\) como la distribución de X, y quiere calcular \(P(a \le X\le b)\), entonces en realidad usa puntuaciones z:

\[P(a \le X\le b) = Pr\left(\frac{a-\mu}{\sigma} \le \frac{X-\mu}{\sigma} \le \frac{b-\mu}{\sigma} \right)\] \[ = Pr\left(z_a \le Z \le z_b \right)\]

Entonces, en otras palabras, en lugar de calcular la probabilidad de que X esté entre a y b, lo que hace es calcular los puntajes z correspondientes de a y b, y los llama \(z_a\) y \(z_b\) y calcula la probabilidad de que Z (una variable con una distribución normal estándar) esté entre \(z_a\) y \(z_b\).

Otra calculadora de distribución normal

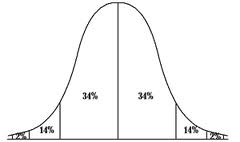
La distribución normal es una distribución continua crucial. Además de esta calculadora de distribución de probabilidad para distribuciones normales, puede usar la Calculadora de la regla 68-95-99 , que muestra cómo usar la regla empírica.

Además, con frecuencia te interesa el comportamiento de los tamaños de muestra, para lo cual puedes utilizar nuestro calculadora de distribución de muestreo , donde está tomando el promedio de muestras de tamaño \(n\)

Otras distribuciones continuas

Para otro tipo de distribuciones continuas, puede probar, por ejemplo. Nuestro sitio ofrece muchas otras calculadoras de distribución continua, como la calculadora de distribución exponencial . F calculadora de distribucion uniforme .