Graficador de funciones trigonométricas

Las funciones trigonométricas tienen la propiedad de repetir su comportamiento. Es decir, son periódicas. Matemáticamente, eso significa que hay un número \(P\) con la propiedad de que

\[f(x+P) = f(x)\]

para todos los valores de \(x\). Ese número \(P\) se llama período . Todo esto está diciendo que el comportamiento de la función se repite en los gráficos trigonométricos cada \(P\) unidades en el eje x.

Observe que para todas las funciones trigonométricas que proporciona para esta calculadora, se supone que el argumento \(x\) es medido en radianes .

Ejemplo de funciones periódicas

Por ejemplo, para el caso de la función seno, \(f(x) = \sin x\), la gráfica se muestra a continuación:

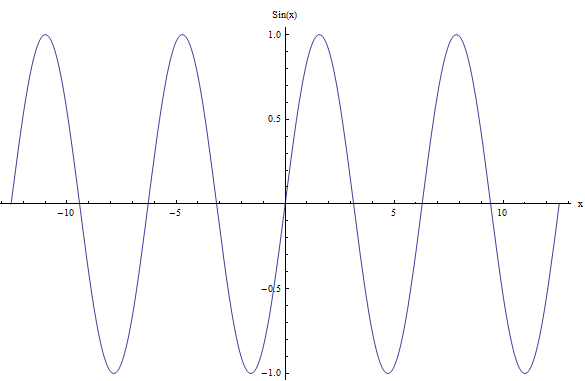
Puede ver que el comportamiento de la función se repite. De hecho, puedes tomar cualquier intervalo de longitud \(2\pi\) y el siguiente intervalo de longitud \(2\pi\) será idéntico al anterior, en términos de la forma de la función.

¿Por qué pasó esto? Porque \(\sin(x + 2\pi) = \sin(x)\), para todo \(x\), y luego la función es periódica.

¿qué puedo graficar con este trazador de funciones trigonométricas?

Puede trazar cualquier función trigonométrica. El uso más común es para graficar seno y coseno, pero puede usarlo para cualquier función trigonométrica.

Verás que las funciones periódicas pueden hacerse más complejas combinándolas con otras expresiones algebraicas.

Por ejemplo, ¿cuál es el comportamiento de la función \(f(x) = 3\sin(2x+1)-4\) Bueno, es incluso periódica? Sí, apuesta. El comportamiento de la función \(f(x) = 3\sin(2x+1)-4\) es similar en todos los sentidos al de la función \(f(x) = \sin x\).

Este graficador de funciones trigonométricas lo ayudará a encontrar el gráfico y las características específicas (período, frecuencia, amplitud, cambio de fase y cambio vertical) de funciones trigonométricas más complejas, como \(f(x) = 3\cos(\pi(x-2)+3)-\frac{\pi}{4}\)

¿importan los paréntesis?

La respuesta corta es: DEPENDE. A veces tendrá una expresión simple donde solo están presentes las sumas o solo las multiplicaciones, en cuyo caso el propiedad asociativa puede ser usado. Pero cuando hay operaciones mixtas con mucha frecuencia no se puede omitir o cambiar un paréntesis sin romper la función o cambiarla.

Calculadoras gráficas

Este graficador solo trata con funciones trigonométricas. Con el fin de graficar otras funciones , puedes usar nuestro trazador de funciones generales , que tomará cualquier función, no solo las trigonométricas.

Ejemplo de gráfico trigonométrico

Pregunta : Considere la función \(f(x) = \sin(3x-2)\). Encuentre el período, la frecuencia, la amplitud y el cambio de fase. Además, proporciona una gráfica de la función.

Solución:

Se ha proporcionado la siguiente función:

\[f(x) = \sin\left(3x-2\right)\]

Con base en el argumento de la función trigonométrica que se pasó, la frecuencia y el período se calculan de la siguiente manera:

\[ \begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{3} \\\\ \\\\ & \approx & 2.0944 \end{array}\]

y también

\[ \begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{3}{2\pi} \\\\ \\\\ & \approx & 0.4775 \end{array}\]

Con base en la función trigonométrica proporcionada, \(f(x) = \sin\left(3x-2\right)\), obtenemos que:

• La amplitud en este caso es \(A = 1\).

• El cambio de fase es igual a \(\displaystyle\frac{2}{3} = 0.6667\).

• El desplazamiento vertical es igual a \( 0\).

En base a la información anterior, se obtiene el siguiente gráfico: