Rationale funktionen

Mit diesem Rechner für rationale Funktionen können Sie die wichtigsten Punkte einer von Ihnen angegebenen rationalen Funktion analysieren, wobei alle Schritte angezeigt werden. In der Regel können Sie für die meisten rationalen Funktionen den Schnittpunkt, die vertikalen Asymptoten und den Graphen finden. Einige spezifische rationale Funktionen haben auch horizontale Asymptoten.

Sie können eine Funktion wie 'f(x)=1/x - x' oder eine Funktion mit Polynomen höheren Grades wie 'f(x) = (x^3-1)/(x^2+x)' angeben

Wenn Sie eine gültige rationale Funktion eingegeben haben, können Sie auf die Schaltfläche "Berechnen" klicken, und Sie erhalten alle Schritte angezeigt.

Eine der wichtigsten Eigenschaften einer rationalen Funktion ist, dass man die Berechnung meist auf das Problem reduzieren kann, dass Polynomgleichungen lösen die eine der "einfachsten" Arten von gleichungen, die Sie lösen können .

Was ist eine rationale funktion?

Eine rationale Funktion ist eine Funktion, bei der die quotient aus zwei Polynomen \(P(x)\) und \(Q(x)\), wobei der Divisor \(Q(x)\) nicht gleich dem Nullpolynom ist. Die Formel für die rationale Funktion lautet also

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \]

Zum Beispiel kann die Funktion

\[\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \]

ist eine rationale Funktion, denn sie ist genau der Quotient zweier Polynome. Aber zum Beispiel

\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{\sin x} \]

ist nicht rational, weil der Divisor kein Polynom ist. Beachten Sie, dass, wenn wir sagen, dass der Divisor \(Q(x)\) nicht gleich dem Nullpolynom ist, wir damit NICHT sagen, dass \(Q(x)\) keine Nullen haben kann. In diesem Fall von \(\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \) ist der Divisor zum Beispiel \(Q(x) = x + 1\), der eine Nullstelle bei \(x = -1\) hat.

Was wir nicht wollen, ist etwas wie

\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{0} \]

denn obwohl in diesem Fall \(Q(x) = 0\) technisch gesehen ein Polynom ist, ist es das Nullpolynom (das überall Null ist).

Schritte zur berechnung einer rationalen funktion

• Schritt 1: Vergewissern Sie sich zunächst, dass Sie eine rationale Funktion haben, für die Sie den Zähler P(x) und den Nenner Q(x) bestimmen können
• Schritt 2: Wenn Sie nicht genau die oben beschriebene Struktur finden, hören Sie auf. Möglicherweise müssen Sie Begriffe gruppieren über algebraische Reduktionen .
• Schritt 3: Sie müssen die reellen Nullstellen von P(x) und Q(x) finden, falls vorhanden. Die gefundenen Schlussfolgerungen stehen in engem Zusammenhang mit den Nullstellen von P(x) und Q(x)
• Schritt 4: Um den y-Achsenabschnitt zu finden, wertet man die Funktion bei Null aus, indem man f(0) berechnet. Der y-Achsenabschnitt ist gut definiert, wenn x = 0 keine Nullstelle von Q(x) ist
• Schritt 5: Um die x-Achsen zu finden, erhält man die Nullstellen von P(x), die nicht Nullstellen von Q(x) sind
• Schritt 6: Um vertikale Asymptoten zu finden, müssen Sie die Nullstellen von Q(x) finden, die nicht Nullstellen von P(x) sind
• Schritt 7: Um horizontale Asymptoten zu finden, muss der Grad von Q(x) größer oder gleich dem Grad von P(x) sein

Es ist zu beachten, dass die Analyse einer rationalen Funktion erwartungsgemäß abhängig ist von Nullen eines Polynoms finden und dann alle Schlussfolgerungen zusammenzufassen. .

Beachten Sie, dass der Bereich einer rationalen Funktion die gesamte reelle Linie ist, mit Ausnahme der Nullstellen des Divisors Q(x). Wenn es eine Nullstelle von Q(x) gibt, die auch eine Nullstelle von P(x) ist, dann kann die Unstetigkeit behoben werden. Der Bereich einer rationalen Funktion hängt von den Graden von P(x) und Q(x) ab.

Warum rationale funktionen verwenden

Rationale Funktionen werden verwendet, weil sie natürliche Erweiterungen von Polynomen sind. Man kann sie als die nächste Stufe der Komplexität einer Funktion betrachten. Wie wir wissen, polynomiale Ausdrücke gehören zu den einfachsten Funktionen, die wir finden können, aber auch zu den nützlichsten.

Rationale Gleichungen tauchen in der Regel bei fortgeschrittenen Mischungsproblemen auf und sind dennoch erstaunlich einfach zu handhaben, vorausgesetzt, die beteiligten Polynome sind einfach genug. Wir wissen wie man quadratische Gleichungen löst für Polynome vom Grad 3 und höher können die Dinge jedoch etwas haariger werden.

Sind polynomfunktionen auch rationale funktionen?

Ja, wenn P(x) ein Polynom ist, dann ist P(x) auch rational, denn wir können schreiben:

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{1} \]

und Q(x) = 1 ist ein echtes Polynom. Umgekehrt gilt das nicht: Eine rationale Funktion ist nicht unbedingt ein Polynom. Warum ist das so? Wenn Q(x) = 1 ist, sind bei \(\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \) natürlich nicht alle Terme freie Terme, wie es die Definition eines Polynoms verlangt.

Formaler ausgedrückt, mit Restsatz haben wir

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} = d(x) + \frac{r(x)}{Q(x)}\]

wobei \(d(x)\) ein Polynom ist, \frac{r(x)}{Q(x)} aber nicht, weil der Grad von r(x) niedriger ist als der Grad von Q(x).

Beispiel: arbeiten mit rationalen funktionen

Finden Sie die Schnittpunkte und Asymptoten und den Graphen von : \(f(x) = \frac{x^2-1}{x+1}\)

Lösung:

Die folgende Funktion wurde uns zur Verfügung gestellt:

\[f\left(x\right)=\frac{x^2-1}{x+1}\]

Wir müssen die Achsenabschnitte und Asymptoten finden, falls vorhanden. Danach wird der Graph der Funktion dargestellt.

Wir wollen die Nullstellen der gegebenen Funktion finden. Wir müssen die folgende rationale Gleichung lösen:

\[\frac{x^2-1}{x+1}=0\]

Beachten Sie, dass wir für \(x \ne -1\) vereinfachen können als:

\[\frac{x^2-1}{x+1} = 0 \Rightarrow \frac{(x-1)(x+1)}{x+1} = 0 \Rightarrow x-1 = 0\]

Hilfszählergleichung

Nun setzen wir den Zähler gleich Null und finden die Lösungen. Dann sind diejenigen Wurzeln, die den Nenner nicht gleich Null machen, Lösungen der rationalen Gleichung.

Die folgende Aufgabe muss gelöst werden, um die Wurzeln des Zählers zu finden: \(x^2-1=0\)

Für eine quadratische Gleichung der Form \(a x^2 + bx + c = 0\) werden die Wurzeln mit Hilfe der folgenden Formel berechnet:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

In diesem Fall ist die Gleichung, die wir lösen müssen, \(\displaystyle x^2-1 = 0\), was bedeutet, dass die entsprechenden Koeffizienten sind:

\[a = 1\] \[b = 0\] \[c = -1\]

Erstens werden wir die Diskriminanz berechnen, um die Art der Wurzeln zu bewerten.Die Diskriminierung wird berechnet als:

\[\Delta = b^2 - 4ac = \displaystyle \left( 0\right)^2 - 4 \cdot \left(1\right)\cdot \left(-1\right) = 4\]

Da die Diskriminante in diesem Fall \(\Delta = \displaystyle 4 > 0\) ist, die positiv ist, wissen wir, dass die Gleichung zwei verschiedene reelle Wurzeln hat.

Stecken Sie diese Werte nun in die Formel für die Wurzeln, die wir erhalten:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{0 \pm \sqrt{\left(0\right)^2-4\left(1\right)\left(-1\right)}}{2\cdot 1} = \displaystyle \frac{0 \pm \sqrt{4}}{2}\]

Also finden wir das:

\[ {x}_1 = \frac{0}{2}-\frac{1}{2}\sqrt{4}=\frac{0}{2}-1=-1 \] \[{x}_2 = \frac{0}{2}+\frac{1}{2}\sqrt{4}=\frac{0}{2}+1=1\]

Hilfsnennergleichung

Wir müssen die Wurzeln des Nenners finden: \(x+1=0\)

Daher führt die Lösung von \(x\) für die gegebene lineare Gleichung zu \(x=-1\).

Zähler und nenner nullen

Nach der oben dargestellten Analyse sind die reellen Nullstellen des Zählers der gegebenen rationalen Funktion \( x_{ 1} = -1\) und \( x_{ 2} = 1\).

Es wird auch festgestellt, dass der Nenner eine reelle Nullstelle hat, nämlich \( x_{ 1} = -1\).

Suche nach x-abschnitten

Ausgehend von den Nullen des Zählers, die keine Nullen des Nenners sind, ergibt sich ein x-Achsenabschnitt, der \(\left(1, 0\right)\) ist.

Suche nach y-achsen

Die Auswertung der unter \(x = 0\) angegebenen Funktion ergibt, dass:

\[ f(0) = \frac{0^2-1}{0+1} = -1\]

der y-Achsenabschnitt ist also \( \left(0, -1\right)\).

Vertikale asymptoten

Nach der Analyse der Nullstellen kommt man zu dem Schluss, dass die Funktion keine vertikalen Asymptoten hat.

Horizontale asymptoten

Man beachte, dass der Grad des Zählers \(2\) und der Grad des Nenners \(1\) ist. Da der Grad des Polynoms im Zähler größer ist als der im Nenner, kann man daraus schließen, dass es keine horizontale Asymptote gibt.

Es ergibt sich das folgende Diagramm:

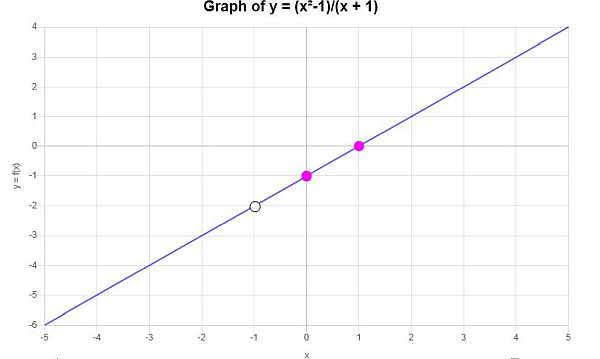
Beispiel: horizontale asymptoten

Hat diese rationale Funktion eine horizontale Asymptote? \(f(x) = \frac{x^2-1}{x^2+1}\)?

Lösung: Es ist klar, dass in diesem Fall die Funktion aus dem Quotienten zweier Polynome besteht, die beide den Grad 2 haben, d. h. sie haben den gleichen Grad, und daher gibt es eine horizontale Asymptote.

Wir können dies auch anhand von Grenzwerten sehen:

\[\lim_{x\to +\infty} f(x) = \lim_{x\to +\infty}\frac{x^2-1}{x^2+1} = \lim_{x\to +\infty}\frac{1-\frac{1}{x^2}}{1+\frac{1}{x^2}} = 1\]

was bedeutet, dass die horizontale Asymptote \(y = 1\) ist. Damit ist die Berechnung abgeschlossen.

Nützliche funktionsrechner

Funktionen sind grundlegende mathematische Objekte, die die Beziehung zwischen verschiedenen Variablen verkörpern. Die Verwendung einer Funktionsrechner kann Ihnen helfen, Funktionen, die zu kompliziert sind, um sie von Hand zu bearbeiten, systematisch zu bearbeiten.

Graphische Darstellung rationaler Funktionen ist eines der häufigsten Spielzeugbeispiele, die Studenten in Algebra und Calculus lernen, und obwohl rationale Funktionen per se vielleicht nicht so oft in Anwendungen auftauchen, können sich die analytischen Fähigkeiten, die für den Umgang mit ihnen erforderlich sind, als unschätzbar erweisen

Das Gleiche gilt für Lösen rationaler Gleichungen hier werden die Prinzipien der Manipulation algebraischer Ausdrücke und deren Reduktion auf ihre niederen Terme für die Erlangung fortgeschrittener Fähigkeiten äußerst hilfreich sein.

Wenn wir nun über die Funktion sprechen, dürfen wir die berechnung der Ableitung einer Funktion , Integration und andere fortgeschrittene Infinitesimaltechniken.