Derivatrechner

Dieser Ableitungsrechner führt Sie durch alle Schritte und Regeln, mit denen Sie die Ableitung einer bestimmten Funktion ermitteln.Sie müssen eine Funktion wie 3x + sin (x^2) eingeben, oder Sie können sie tatsächlich mit der gesamten Funktionsdefinition wie f (x) = 3x^2 + 2tan (x^3) vornehmen.

Beachten Sie, dass dieser Rechner als Rechner für die erste Ableitung bezeichnet werden kann, genauso wie als Rechner für die Ableitung. Die erste Ableitung und die Ableitung stellen dasselbe dar, und der "erste" Teil wird normalerweise weggelassen.

Die bereitgestellte Funktion kann vollständig vereinfacht werden oder nicht. Sie spielt keine Rolle, da der Taschenrechner die Funktion zuerst vereinfacht, falls dies erforderlich ist, bevor er sein Ableitungen berechnet.

Einmal Gültige Funktion Wenn Sie bereitgestellt wurden, müssen Sie nur auf "Berechnen" klicken, einige Sekunden warten und alle Schritte der Berechnung werden Ihnen präsentiert.

Die Differenzierung ist das Hauptwerkzeug der Infinitesimalrechnung (zusammen mit der Integration) und ist eine wichtige Operation, die in der fortgeschrittenen Mathematik weit verbreitet ist. Einige sehr häufige Anwendungen sind tangentenlinienberechnung , Maxima und Minima und vieles mehr.

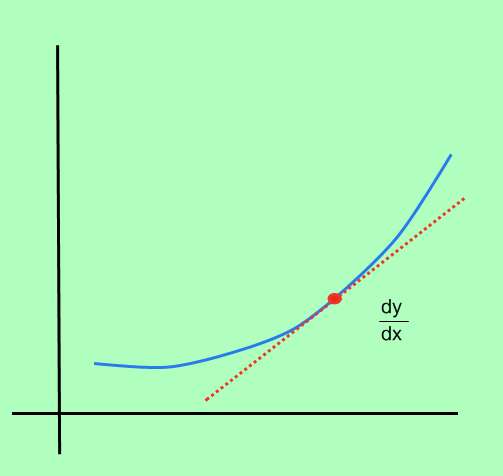
Wie berechnet man die ableitung einer funktion?

Der Prozess der Berechnung der Ableitung einer Funktion wird aufgerufen Unterschied und es besteht darin, die sofortige Änderungsrate des Punktes an jedem Punkt im Bereich der Funktion zu bestimmen.

Wie hoch ist die sofortige Änderungsrate einer Funktion?Beginnen wir mit der Definition von Änderungsrate : Betrachten Sie eine Funktion \(f\), und nehmen Sie an, dass wir zwei Punkte haben, \(x_0\) und \(x_1\). Am Punkt \(x_0\) hat die Funktion den Wert \(f(x_0)\), und am Punkt \(x_1\) nimmt die Funktion den Wert \(f(x_1)\) an

Dann wird die Änderung von f als \(\Delta y = f(x_1) - f(x_0)\) definiert (was auch als Änderung von y bezeichnet wird). Auch die Änderung von x ist definiert als \(\Delta x = x_1 - x_0)\). In einfachen Worten: \(\Delta x\) ist die Änderung von x, während \(\Delta y\) die Änderung des Funktionswerts aufgrund der Änderung von x ist.

Grafisch:

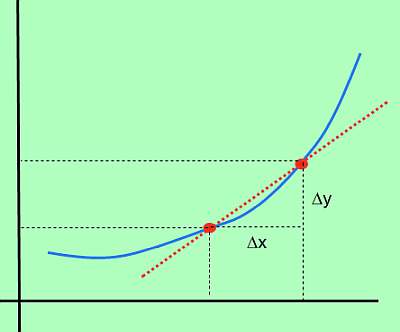
Ableitungsformel

Wenn also \(\Delta x\) für die Änderung von x und \(\Delta y\) für die Änderung des Funktionswerts aufgrund der Änderung von x steht, sind die entsprechenden Änderungsrate Ist:

\[\text{Rate of Change} = \displaystyle \frac{\Delta y}{\Delta x} \]

Was wäre dann die unmittelbare Änderungsrate? Das entspräche der Analyse, was passieren würde, wenn \(\Delta x\) wirklich klein wird. Man würde erwarten, dass \(\Delta y\) auch klein wird, aber was würde mit der Rate zwischen \(\Delta y\) und \(\Delta x\) passieren?

In diesem Zusammenhang wird also die sofortige Änderungsrate definiert als

\[\text{Instant Rate of Change} = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} \]

Laienhaft ausgedrückt, setzen wir also \(x_0\) fest und berechnen die Änderungsrate für Werte von \(x_1\), die immer näher an \(x_0\) liegen. Mit dieser Idee der momentanen Änderungsrate können wir die folgende Formel für die Ableitung an einem Punkt \(x_0\) angeben.

\[f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \]

Wenn der obige Grenzwert existiert, sagen wir, dass die Funktion f differenzierbar ist bei \(x_0\). Wir sagen auch, dass eine Funktion an einer Menge A differenzierbar ist, wenn die Funktion an jedem Punkt der Menge differenzierbar ist.

Schritte für die verwendung der ableitungsformel

• Schritt 1: Identifizieren Sie deutlich die Funktion f, die Sie unterscheiden möchten
• Schritt 2: Stellen Sie sicher, dass Sie F so weit wie möglich vereinfachen, da ansonsten die erforderliche Grenze unnötig schwieriger sein kann
• Schritt 3: Entscheiden Sie, ob Sie mit einem generischen Punkt X0 arbeiten oder einen bestimmten numerischen Punkt für X0 geben
• Schritt 4: Verwenden Sie auf der Grundlage der Definition der Funktion die Formel \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \). Das heißt, man setzt die Werte von x0 und x1 in f ein und schaut, wie die Formel algebraisch aussieht
• Schritt 5: Vereinfachen Sie so viel wie möglich, bevor Sie die Grenze nehmen
• Schritt 6: Manchmal leichter, x1 = x0 + h festzulegen, und dann das Limit als H -Konversation auf 0 berechnen

Beachten Sie, dass Schritt 6 eine ist, die manche Leute als Standard mögen.In der Tat lautet die alternative Ableitungsformel, die für die Vereinfachung einfacher erscheinen mag,:

\[f'(x_0) = \displaystyle \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h} \]

Welches ist die Formel, die Sie in Ihrem Lehrbuch finden, anstatt in der anderen.

Ableitungsregeln

Es scheint ein verdammt viel Arbeit, das Derivat mithilfe der Formel zu berechnen.Und in der Tat könnte es ein mühsamer Prozess sein, wenn wir uns entschlossen haben, jeden Differenzierungsprozess mit der Derivatformel auszuarbeiten.

Glücklicherweise gibt es eine Reihe von Funktionen (nämlich Polynom , Trigonometrische Funktionen ) für die wir mit Genauigkeit wissen, was ihre Derivat ist.

Darüber hinaus haben wir Differenzierungsregeln Das ermöglicht es uns, die Ableitung einer Funktion zu finden, die a ist Zusammenesetzte Fungion und/oder eine Kombination von Elementarfunktionen (für die wir ihre Ableitung kennen) in Bezug auf Elementarderivate.

Was sind schritte zur berechnung des derivats?

• Schritt 1: Identifizieren Sie die Funktion f Sie möchten differenzieren.Vereinfachen Sie so viel wie möglich vor der Berechnung der Ableitung
• Schritt 2: Stellen Sie fest, ob Sie die Ableitungsformel verwenden müssen oder nicht
• Schritt 3: Wenn Sie die Ableitungsformel verwenden müssen, verwenden Sie \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \), oder Sie können \(f'(x_0) = \displaystyle \lim_{h \to 0}\frac{f(x_0+h) - f(x_0)}{h} \) verwenden, wenn Ihnen dies einfacher erscheint
• Schritt 4: Wenn Sie nicht die Ableitungsformel verwenden müssen, können Sie die Hauptdifferenzierungsregeln verwenden: Linearität, Produktregel , Quotienteregel und Kettenregel , die Ihnen helfen, die Berechnung des Derivats für die Verwendung bekannter Ableitungen zu verringern

Oftmals die Funktion, die Sie versuchen, Funde sie Dasivat Denn ist keine einfache Funktion, aber es ist eine grundlegende Kombination mehrerer einfacher Funktionen.Zum Beispiel die Funktion

\[f(x) = x + \cos(x) + \sin(x)\]

ist an sich keine elementare Funktion, aber sie ist Zusammenesetzte Fungion von drei elementaren Funktionen, \(x\), \(\sin x\) und \(\cos x\).

Anwendungen von derivaten

Man könnte denken "Nun, Derivate beinhalten Grenzen und das ist super theoretisch, also darf es nicht zu viele Anwendungen haben", aber Sie wären völlig falsch.Die Magie der Derivate ist, dass es sich im Wesentlichen um die Änderungsrate von Funktionen handelt, die verschiedene Arten von Prozessen darstellen können.

Aus diesem Grund ermöglicht die Differenzierung den Veränderungsprozess und den Vergleich ändernder Variablen, was eine breite Anwendbarkeit hat.

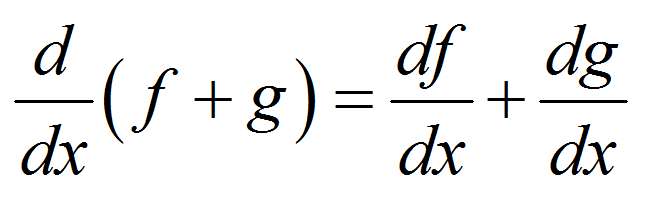
Beispiel: berechnung des derivats

Berechnen Sie die Ableitung nach x für \(f(x) = \displaystyle \frac{x}{3} + \frac{5}{4} \cos(x) - \frac{5}{4} \sin(x^2)\)

Lösung: Die folgende Funktion wurde bereitgestellt: \(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\), für die wir ihre Ableitung berechnen müssen.

Erstschritt: In diesem Fall müssen wir zunächst die gegebene Funktion \(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right) \) vereinfachen, und dazu führen wir die folgenden Vereinfachungsschritte durch:

Nach der Vereinfachung der Funktion können wir mit der Berechnung des Derivats fortfahren:

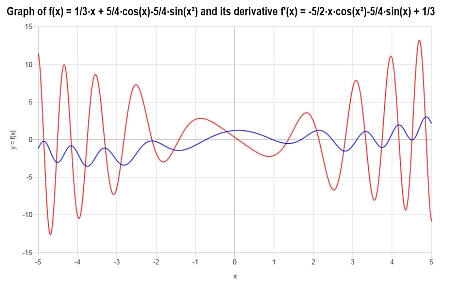
Die folgende Darstellung ergibt sich für \(\displaystyle f(x)=\frac{1}{3}x+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\) auf dem Intervall \([-5, 5]\):

Beispiel: differenzierung einer funktion

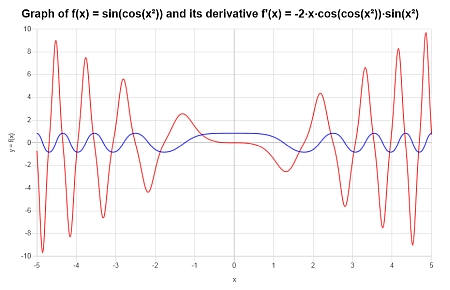
Berechnen Sie die Ableitung von : \(f(x) = \sin(\cos(x^2))\), und geben Sie den Graphen von \(f(x)\) und \(f'(x)\) an.

Lösung: Jetzt haben wir \(\displaystyle f(x)=\sin\left(\cos\left(x^2\right)\right)\).

Die Funktion wurde bereits vereinfacht, so dass wir direkt zur Berechnung ihrer Ableitung übergehen können. Durch die Verwendung dieser Ableitung cal erhalten wir:

Daraus ergibt sich die folgende Darstellung für die Funktion auf dem Intervall \([-5, 5]\):

Beispiel: derivatrechner

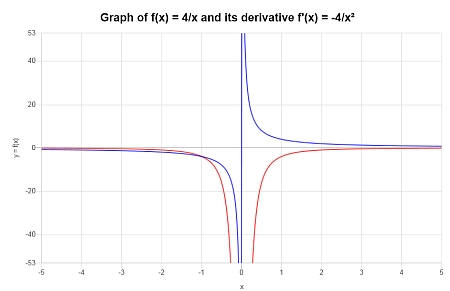
Finden Sie die Ableitung von \( f(x) = \displaystyle \frac{4}{x}\). Ist sie überall wohldefiniert? Zeichnen Sie sie.

Lösung: Die Funktion, für die die Ableitung benötigt wird, ist \(\displaystyle f(x)=\frac{4}{x}\).

Es ist keine weitere Vereinfachung erforderlich, sodass wir direkt sein Derivat berechnen können:

Grafisch:

Mehr über derivate und funktionen

Diese derivat-Rechner mit Stufen wird sich für Sie als sehr nützlich erweisen, da es die Berechnung der Ableitung einer beliebigen Funktion durchführt und alle Schritte des Prozesses anzeigt, wobei die entsprechenden Fähigkeitsregeln und Ihnen mitteilen, wann und warum sie angewendet werden.

Dieser Rechner kann auch aufgerufen werden dy dx-Rechner oder differentialquotienten-Rechner denn genau das tut es, es berechnet den Grenzwert des Verhältnisses dy/dx, wenn dx gegen 0 geht.

Funktionen sind extrem wichtige Konstrukte in der Mathematik. Neben der Differenzierung müssen Sie in der Lage sein Vereinfachensier -Funktion Normalerweise als Präambel anderer spezialisierterer Berechnungen.Es gibt spezielle Arten von Funktionen, mit denen Sie bestimmte Vorgänge durchführen können, z. B. das, was Sie mit Polynomoperation .

Interessanterweise viele wichtige Elemente wie das Finden der Koordinaten der Scheitelpunkt Einer Parabel Dies kann auf clevere Weise unter Verwendung geometrischer Argumente abgeleitet werden, kann unter Verwendung der Differenzierung trivial erhalten werden.

Auch die Idee der Tangente und Annauerung Erster Ordnung ergeben sich auf natürliche Weise aus dem Konzept der Ableitung und sind eine natürliche Erweiterung.