Löser Algebra

Trigendrechner

Anweisungen: Verwenden Sie den Trig -Taschenrechner, um den von Ihnen bereitgestellten trigonometrischen Ausdruck zu berechnen und zu bewerten. Bitte geben Sie den TRIG -Ausdruck ein, den Sie berechnen möchten, oder eine Trig -Funktion, die Sie analysieren möchten, in der folgenden Formularbox.

Mehr zu diesem trig -taschenrechner

Dies Trigendrecht Ermöglichen Sie Ihnen, jeden von Ihnen bereitgestellten Trig -Ausdruck zu bewerten.Stellen Sie sicher, dass Sie einen gültigen trigonometrischen Ausdruck anbieten, es kann etwas direktes wie cos (pi/2) sein, oder es könnte etwas sein, das nicht vollständig vereinfacht wird, wie Sünde (1/3*PI+3/4*PI).

Sie können auch eine TRIG -Funktion wie sin (1/3*pi x + 3/4*pi + x) bereitstellen, und dieser Taschenrechner analysiert und nach Möglichkeit die entsprechende Zeit, Frequenz usw. zusammen mit seinem Graph .

Sobald ein gültiger Trig -Ausdruck bereitgestellt wurde, müssen Sie lediglich auf "Berechnen" klicken, und alle Schritte der Berechnung werden Ihnen angezeigt.

Trigonometrische Austrücke sind ziemlich notwendig, besonders wenn Sie sind Dreickke Lösen .Normalerweise ist es einfach, jede Trig -Berechnung auf die Berechnung einiger bemerkenswerter Winkel für die zu reduzieren Kosinus und Sinus .

Wie mache ich trig -berechnungen?

Eine TRIG -Berechnung kann eine sehr allgemeine und umfassende Aufgabe sein, die möglicherweise bestimmte Strategien aufweist, die je nach der spezifischen Trig -Berechnung, die Sie tun müssen, und den TRIG -Funktionen am besten funktionieren, aber es gibt einige allgemeine Strategien, die Ihnen gut dienen können.

Was sind die schritte für eine trig -berechnung?

Schritt 1: Identifizieren Sie klar den Trig -Ausdruck, den Sie berechnen möchten, und vereinfachen Sie die Zahlen und den Bruch so viel wie möglich.Wenn Sie beispielsweise COS (1+1/2) haben, werden Sie zunächst feststellen, dass 1+1/2 = 3/2, sodass Sie tatsächlich COS (3/2) benötigen, also benötigen Sie tatsächlich (3/2).
Schritt 2: Sobald mögliche Brüche und einfache Zahlen gruppiert und betrieben werden, stellen Sie fest, ob es andere Triggfunktionen als Sünde und Cosinus gibt.Wenn es gibt, drücken Sie alles in Sinus und Cosinus aus
Schritt 3: Gehen Sie nun alle Teile durch, die jetzt nur Sinus und beinhalten Kosinus und beurteilen Sie, ob es bemerkenswerte Winkel gibt, die Multiplikatoren oder Brüche von π beinhalten
Schritt 4: Bewerten Sie diese Ausdrücke direkt mit bemerkenswerten Winkel Das kann vereinfacht werden.Diejenigen, die nicht direkt vereinfacht werden können (falls vorhanden), wie es ist, oder liefern eine approximierte ( Abgerundeter Wert ) von ihnen

Es ist üblich zu gehen, wie sie sind Ausdrucke Das haben keine einfachen Vereinfachungen gewusst.Zum Beispiel hat COS (1/4) keine einfache Reduzierung, so dass es normalerweise so bleibt, wie es ist.Aber zum Beispiel cos (π/3) = 1/2, so dass so einfache Reduktionen offensichtlich durchgeführt werden

Trigonometrierechner mit schritten

Der Vorteil von Dieser Taschenrechner ist, dass es Ihnen alle relevanten Schritte des Prozesses zeigt.Der Prozess ist einfach: Es geht darum Ausdrucke Vereinfachen Dies beinhaltet nur Zahlen, Brüche und insgesamt direkt evaluierbare numerische Ausdrücke.

Dann und nur dann sollten Sie sich für die Trig -Berechnung entscheiden, um die Dinge so viel wie möglich zu beseitigen, bevor Sie eine Trig -Berechnung versuchen.

Vorteile der verwendung einer trigonometrischen taschenrechner -app

Sie mögen denken, na ja, ich weiß ziemlich gut, dass meine Trig -Funktionen für grundlegende bemerkenswerte Winkel funktioniert, also brauche ich keine Trig -Taschenrechner -App.Das mag durchaus der Fall sein, obwohl Sie vielleicht ein bisschen zögern, dass Sie mit etwas wie \(\sin\left(\displaystyle\frac{345}{11}\pi\right)\) .... können Sie es vereinfachen?Ist es ein bemerkenswerter Winkel?

Es ist wirklich eine gute Sache, zu versuchen, Dinge von Hand zu lösen und Ihr trigonometrisches Gedächtnis auszuüben, aber a Trig -Rechner -App Kann Ihnen zumindest helfen, Ihre Antworten zu überprüfen.

Beispiel: trig -berechnung

Berechnen Sie den TRIG -Ausdruck: \(\sin\left(\frac{5}{4}\pi\right)\)

Lösung: Der folgende trigonometrische Ausdruck wurde bereitgestellt, um berechnet zu werden:

\[ \sin\left(\frac{5\pi}{4}\right)\]

Durch die Überprüfung des gegebenen trigonometrischen Ausdrucks können wir einen bemerkenswerten Winkel finden, nämlich \(\sin\left(\frac{5\pi{}}{4}\right)\).

▹ Für den Winkel \(\frac{5\pi{}}{4}\) wir bekommen grafisch:

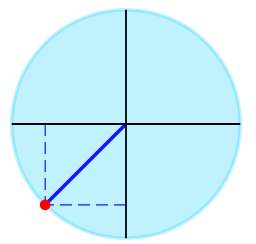
Der angegebene trigonometrische Ausdruck kann vereinfacht werden als:

\( \displaystyle \sin\left(\frac{5\pi{}}{4}\right)\)

Evaluating the trigonometric expression at the notable angle \(\displaystyle\frac{5\pi{}}{4}\) we get that: \(\displaystyle \sin\left(\frac{5\pi{}}{4}\right) = -\frac{ \sqrt{2}}{ 2}\)

\( = \,\,\)

\(\displaystyle -\frac{ \sqrt{2}}{ 2}\)

Fazit: Wir schließen daraus, dass \(\displaystyle \sin\left(\frac{5\pi}{4}\right) = -\frac{1}{2}\sqrt{2} \approx -0.7071\).

Beispiel: verwenden des trigendrechners

Reduzieren: \(\displaystyle \cos\left(\frac{1}{3} + \frac{5}{4}\right)\)

Lösung: Jetzt müssen wir daran arbeiten:

\[ \cos\left(\frac{1}{3}+\frac{5}{4}\right)\]

Dieser trigonometrische Begriff kann wie folgt vereinfacht werden:

\( \displaystyle \cos\left(\frac{1}{3}+\frac{5}{4}\right)\)

Grouping and operating all the integer terms and fractions: \(\displaystyle \frac{ 1}{ 3}+\frac{ 5}{ 4}=\frac{ 1}{ 3} \times \frac{ 4}{ 4}+\frac{ 5}{ 4} \times \frac{ 3}{ 3}=\frac{ 4+5 \times 3}{ 12}=\frac{ 4+15}{ 12}=\frac{ 19}{ 12}\)

\( = \,\,\)

\(\displaystyle \cos\left(\frac{19}{12}\right)\)

Fazit: Es wird geschlossen, dass \(\displaystyle \cos\left(\frac{1}{3}+\frac{5}{4}\right) = \cos\left(\frac{19}{12}\right) \approx -0.0125\).

Beispiel: trig -vereinfachung

Berechnen Sie \( \sin\left(\frac{2}{3} \times \frac{6}{5} \pi\right)+ \frac{2}{5}\cdot \cos(\frac{\pi}{4}) \).

Lösung: Durch die Überprüfung des gegebenen trigonometrischen Ausdrucks können wir einen bemerkenswerten Winkel finden, nämlich \(\cos\left(\frac{\pi{}}{4}\right)\).

▹ Für den Winkel \(\frac{\pi{}}{4}\) wir bekommen grafisch:

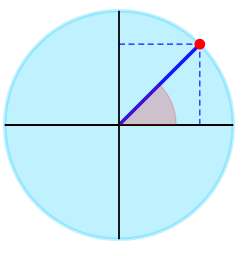
Der angegebene trigonometrische Ausdruck kann vereinfacht werden als:

\( \displaystyle \sin\left(\frac{2}{3}\cdot\frac{6}{5}\pi{}\right)+\frac{2}{5}\cos\left(\frac{\pi{}}{4}\right)\)

Evaluating the trigonometric expression at the notable angle \(\displaystyle\frac{\pi{}}{4}\) we get that: \(\displaystyle \cos\left(\frac{\pi{}}{4}\right) = \frac{1}{2}\sqrt{2}\)

\( = \,\,\)

\(\displaystyle \sin\left(\frac{2}{3}\cdot\frac{6}{5}\pi{}\right)+\frac{2}{5}\cdot\frac{1}{2}\sqrt{2}\)

Grouping and operating all the integer terms and fractions: \(\displaystyle \frac{ 2}{ 3} \times \frac{ 6}{ 5}=\frac{ 2 \times 6}{ 3 \times 5}=\frac{ 2 \times (\cancel{3} \times 2)}{ \cancel{3} \times 5}=\frac{ 2 \times 2}{ 5}=\frac{ 4}{ 5}\)

\( = \,\,\)

\(\displaystyle \sin\left(\frac{4}{5}\pi{}\right)+\frac{2}{5}\cdot\frac{1}{2}\sqrt{2}\)

Evaluating the trigonometric expression at the notable angle \(\displaystyle\frac{4}{5}\pi{}\) we get that: \(\displaystyle \sin\left(\frac{4}{5}\pi{}\right) = \frac{1}{4}\sqrt{-2\sqrt{5}+10}\)

\( = \,\,\)

\(\displaystyle \frac{1}{4}\sqrt{-2\sqrt{5}+10}+\frac{\frac{2}{5}\cdot1}{2}\sqrt{2}\)

Grouping and operating all the integer terms and fractions: \(\displaystyle \frac{ 2}{ 5} \times \frac{ 1}{ 2}=\frac{ 2}{ 5 \times 2}=\frac{ \cancel{2}}{ 5 \times \cancel{2}}=\frac{ 1}{ 5}\)

\( = \,\,\)

\(\displaystyle \frac{1}{4}\sqrt{-2\sqrt{5}+10}+\frac{1}{5}\sqrt{2}\)

Fazit: Wir schließen daraus, dass \(\displaystyle \sin\left(\frac{2}{3}\cdot\frac{6}{5}\pi\right)+\frac{2}{5}\cos\left(\frac{\pi}{4}\right) = \frac{1}{5}\sqrt{2}+\frac{1}{4}\sqrt{-2\sqrt{5}+10} \approx 0.8706\).

Weitere geometrierechner

Die Arbeit mit TRIG -Funktionen ist eng mit der Arbeit mit Dreiecken verbunden. Bei der Arbeit mit a also Dreckksrechner Sie werden viele Trig -Berechnungen finden.