Löser Infinitesimalrechnung

Quotientenregel

Anweisungen: Verwenden Sie diesen Quotientenregel -Rechner, um die Ableitung der Funktion zu ermitteln, die von Ihnen bereitgestellte Quotienten umfasst und alle Schritte angezeigt.Bitte geben Sie die Funktion im folgenden Formularfeld ein.

Die quotientenregel

Mit diesem Taschenrechner können Sie die Quotientenregel für eine Funktion verwenden, die einen Quotienten beinhaltet, der alle Schritte des Prozesses zeigt.Alles, was Sie bereitstellen müssen, ist eine gültige differenzierbare Funktion.Diese Funktion muss mindestens einen Quotienten beinhalten, damit die Quotientenregel anwendbar ist.

Ein Beispiel für eine gültige Funktion wäre f (x) = (x^2 + 2x + 1)/(x^2-1) oder so etwas wie f (x) = sin (x)/x usw.

Sobald eine gültige Funktion mit Quotienten bereitgestellt wird, müssen Sie auf die Schaltfläche "Berechnen" klicken, um die Schritte der angezeigten Berechnung zu erhalten.

Zusammen mit Produktregel und Kettenregel , das Quotienteregel ist eine der wichtigsten Grundlagen Fähigkeitsregeln .

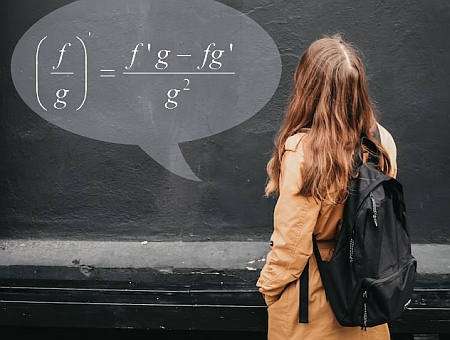
Quotientenregelformel

In einfachen Worten die Quotienteregel Hilft Ihnen, die Ableitung eines Quotienten zu berechnen, indem Sie das Wissen der einzelnen Funktionen und ihrer Derivate verwenden.Die Quotientenregel -Formel lautet:

\[\displaystyle \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \displaystyle \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} \]

Was sind die schritte zur verwendung der quotientenregel?

Schritt 1: Identifizieren Sie klar die Funktionen F (x) und g (x), die in den Zähler und Nenner des Quotienten eingehen
Schritt 2: Vereinfachen Sie jeden offensichtlichen Begriff, der vereinfacht werden kann
Schritt 3: Berechnen Sie die entsprechenden Derivate f '(x) und g' (x)
Schritt 4: Schließen Sie die in Schritt 3 gefundenen Werte in der Formel \(\displaystyle \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \displaystyle \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} \)

Beachten Sie, dass F (x) und g (x) möglicherweise noch komplexe Funktionen sein können. Sie müssen daher möglicherweise andere Regeln wie die Kettenregel verwenden, um sowohl F '(x) als auch g' (x) zu berechnen.

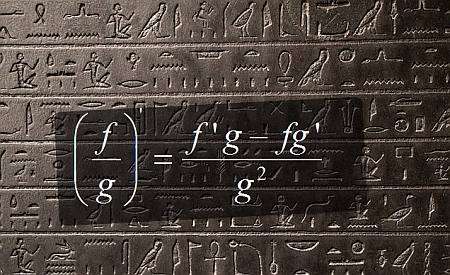
Quotientenregel derivat

Wenn Sie ein Quotientenregelderivat berechnen, reduzieren Sie die Ableitung eines Quotienten auf das Wissen der einzelnen Derivate, aber diese einzelnen Derivate benötigen möglicherweise noch viele Schritte mit Grunddlegende Thelitungsregeln gelöst werden.

Deshalb wird die Differenzierung als „unkomplizierte“ Operation angesehen, aber dennoch müssen Sie alle Teile, die beim Zersetzen mit Derivatregeln entstehenangewandt.

Sie können also einen iterativen Prozess haben, aber es wird garantiert, dass es irgendwann endet, indem Sie tiefer in jeden kleineren Teil eingehen, bis Sie ein elementares Derivat finden Polynom oder ein Trig -Dederivat .

Quotientenregel in der differenzierung

Die Rolle der Rolle der Quotienteregel in der differenzierung ist ziemlich wichtig, ein guter Grund, warum Sie dafür einen Taschenrechner verwenden möchten.In algebraischen Begriffen könnte die Quotientenregel als gewundener angesehen werden als die Produktregel, und sie könnte in vielen Fällen wahr sein, hängt jedoch letztendlich von der Komplexität der Funktionen im Zähler und des Nenners ab.

Beispiele für quotientenregel

Betrachten Sie die Funktion: \(f(x) = \frac{x^2+1}{x-2}\), finden Sie ihre Ableitung.

Lösung: In diesem Beispiel müssen wir die Funktion \(\displaystyle f(x)=\frac{x^2+1}{x-2}\) analysieren, um dasivat zu finden.

\( \displaystyle \frac{d}{dx}\left(\frac{x^2+1}{x-2}\right)\)

By using the Quotient Rule: \(\frac{d}{dx}\left( \frac{x^2+1}{x-2} \right) = \frac{\left(x-2\right) \cdot \frac{d}{dx}\left(x^2+1\right)-\left(x^2+1 \right) \cdot \frac{d}{dx}\left(x-2\right)}{\left(x-2\right)^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \cdot \frac{d}{dx}\left(x^2+1\right)-\left(x^2+1 \right) \cdot \frac{d}{dx}\left(x-2\right)}{\left(x-2\right)^2}\)

By linearity, we know \(\frac{d}{dx}\left( x-2 \right) = \frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(2\right)\) and \(\frac{d}{dx}\left( x^2+1 \right) = \frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\right)-\left(x^2+1 \right) \left(\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(2\right)\right)}{\left(x-2\right)^2}\)

Since the derivative of a constant is 0, we get that:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)\right)-\left(x^2+1 \right) \left(\frac{d}{dx}\left(x\right)\right)}{\left(x-2\right)^2}\)

We already know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)\right)-\left(x^2+1 \right)}{\left(x-2\right)^2}\)

In this case we use the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \left(2x\right)-\left(x^2+1 \right)}{\left(x-2\right)^2}\)

and then we get

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2x\left(x-2\right)-\left(x^2+1\right)}{\left(x-2\right)^2}\)

Note that \((2x) \cdot (x-2) = 2x^2-2\cdot 2x = 2x^2-4x\), as we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2x^2-4x-\left(x^2+1\right)}{\left(x-2\right)^2}\)

Removing unnecessary parentheses and multiplying the terms by \(-1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2x^2-4x-x^2-1}{\left(x-2\right)^2}\)

Aggregating those terms with \(x^2\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{-4x+\left(-1+2\right)x^2-1}{\left(x-2\right)^2}\)

Putting together the numerical values and operating the terms that were grouped with \(x^2\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{-4x+x^2-1}{\left(x-2\right)^2}\)

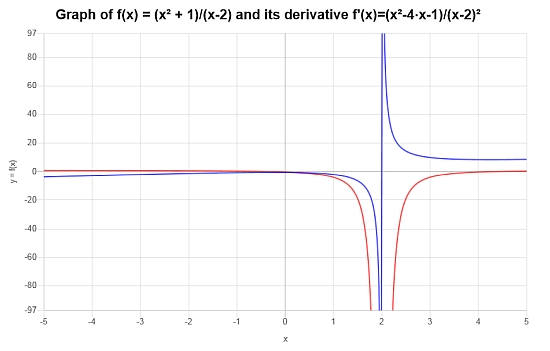
Fazit : Wir finden, dass die Ableitung der angegebenen Funktion lautet:

\[f'(x) = \frac{x^2-4x-1}{\left(x-2\right)^2}\]

Die grafische Darstellung der Funktion und ihres Ableitung lautet also \([-5, 5]\):

Beispiel: quotientenregelberechnung

Betrachten Sie nun \(f(x) = \frac{x}{\sin(x)}\), finden Sie ihre Ableitung mit der Quotientenregel.

Lösung: Für dieses zweite Beispiel ist die Funktion, an der wir interessiert sind, \(\displaystyle f(x)=\frac{x}{\sin\left(x\right)}\).Lassen Sie es mit der Quotientenregel unterscheiden.

\( \displaystyle \frac{d}{dx}\left(\frac{x}{\sin\left(x\right)}\right)\)

Using the Quotient Rule: \(\frac{d}{dx}\left( \frac{x}{\sin\left(x\right)} \right) = \frac{\sin\left(x\right) \cdot \frac{d}{dx}\left(x\right)-x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\sin\left(x\right) \cdot \frac{d}{dx}\left(x\right)-x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)

We already know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\sin\left(x\right) -x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)

Directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\sin\left(x\right) -x\cdot \cos\left(x\right)}{\sin\left(x\right)^2}\)

so then we get that

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\sin\left(x\right)-x\cos\left(x\right)}{\sin\left(x\right)^2}\)

By reorganizing/simplifying/expanding the terms that are amenable to

\( \displaystyle = \,\,\)

\(\displaystyle \frac{-\left(x\cos\left(x\right)-\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)

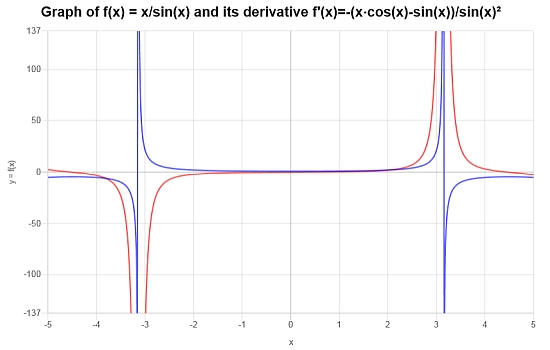
Fazit : Die Schlussfolgerung ist, dass die Ableitung basierend auf der obigen Berechnung angegeben wird durch:

\[f'(x) = \frac{-\left(x\cos\left(x\right)-\sin\left(x\right)\right)}{\sin\left(x\right)^2}\]

Grafisch können wir die Funktion (in blau) und ihre Ableitung (in Rot) sehen:

Weitere beispiele für quotientenregel

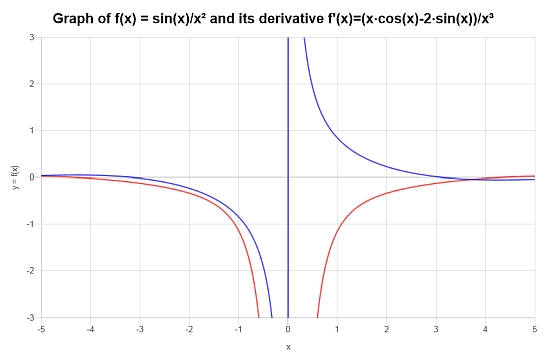
Betrachten Sie schließlich die Funktion: \(f(x) = \frac{\sin(x)}{x^2}\), finden Sie ihre Ableitung.

Lösung: Für dieses endgültige Beispiel für Quotientenregel arbeiten wir mit der Funktion \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x^2}\)..

\( \displaystyle \frac{d}{dx}\left(\frac{\sin\left(x\right)}{x^2}\right)\)

The Quotient Rule applies: \(\frac{d}{dx}\left( \frac{\sin\left(x\right)}{x^2} \right) = \frac{\left(x^2\right) \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x^2\right)}{\left(x^2\right)^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x^2\right) \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x^2\right)}{\left(x^2\right)^2}\)

We use the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\) and directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x^2\right) \cdot \cos\left(x\right)-\sin\left(x\right)\cdot 2x}{\left(x^2\right)^2}\)

which then leads to

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\cos\left(x\right)\cdot x^2-\sin\left(x\right)\cdot 2x}{x^4}\)

By simplifying and regrouping terms

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x\cos\left(x\right)-2\sin\left(x\right)}{x^3}\)

Fazit : Für die angegebene Funktion ist das Ableitungen:

\[f'(x) = \frac{x\cos\left(x\right)-2\sin\left(x\right)}{x^3}\]

Die folgende Grafik zeigt die Situation für \(f\) und \(f'\):

Mehr derivatrechner

In Kalkül wirst du Funde Sie Können Können Überall, wo du dich ansiehst.Es gibt Tausende von Anwendungen, bei denen sie die wichtigsten Instrumente für Wissenschaft und Ingenieurwesen betreffen.

Sie müssen etwas lernen Implizit -Unterschied Für verschiedene Anwendungen, die häufig verwandte Raten oder in multivariatem Kalkül beteiligt sind, werden Sie interessiert sein Teilendeivate Funde .

Insgesamt finden Sie Ihr Leben leichter, wenn Sie mit Derivaten umgehen, wenn Sie in der Lage sind, die häufigsten Fähigkeitsregeln , einschließlich der Kettenregel auch die Produktregel und Quotienteregel .