Über diesen tangential -leitungsrechner

Mit diesem Rechner können Sie die Berechnungen, die erforderlich sind, um die Tangentenlinie einer Funktion zu erhalten, an einem bestimmten Punkt nahtlos durchzuführen, die alle Schritte anzeigen.

Sie müssen lediglich eine gültige Funktion F (x) und einen Punkt bereitstellen, an dem Sie die Tangentenlinie möchten.Die Funktion kann eine gültige, differenzierbare Funktion wie f (x) = sin (x) oder f (x) = x^2 - x + 1 usw. sein. Der Punkt kann jeder gültige numerische Ausdruck sein, wie 1/2 fürBeispiel.

Wenn dann die erforderlichen Informationen bereitgestellt und gültig sind, müssen Sie auf "Berechnen" klicken, um alle Schritte der Tangentenliniengleichung zu erhalten.

Tangentenlinienanwendungen in der Wissenschaft sind in der Nähe reichlich vorhanden.Auch genannt Erste Ordnung -Oden -Lineare Annauerung Es hat eine wirklich tiefe Bedeutung in der Physik und Ingenieurwesen, bei denen die Idee des Hauptbeitrags zum Veränderung (dem Teil erster Ordnung) eine viele Informationen über einen Prozess enthüllt.

Was ist die tangentenlinie?

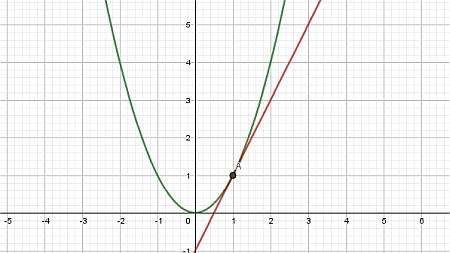
Vereinfacht ausgedrückt, ist eine Tangente eine Linie, die eine Kurve schneidet, aber nur in einem Punkt (zumindest lokal). Diese Tangente wird konstruiert, indem man einen Punkt \(x_0\) festlegt und dann einen anderen Punkt \(x_1\) nimmt.

Wenn man dann die Linie konstruiert, die durch die Punkte \((x_0, f(x_0))\) und \((x_1, f(x_1))\) verläuft, erhält man eine sogenannte Sekantenlinie , wie in der Grafik unten gezeigt:

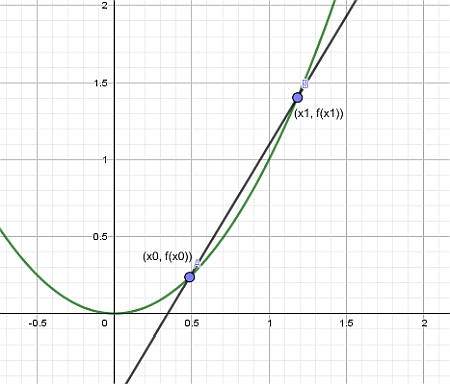
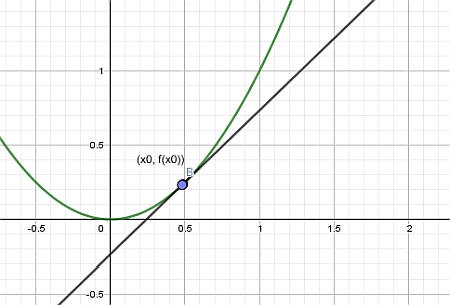
Schließlich lassen wir den Punkt \(x_1\) sich dem Punkt \(x_0\) nähern, und wir erhalten die Tangente:

Schritte zum finden der tangentenlinie geometrisch

• Schritt 1: Identifizieren Sie die Funktion f (x), mit der Sie arbeiten möchten, und den Punkt X0.Sie brauchen beide
• Schritt 2: Der Punkt (x0, f (x0)) befindet sich auf der Kurve der Funktion f (x).Planen Sie es
• Schritt 3: Wählen Sie einen Punkt (x1, f (x1)) für einen x1, der sich von x0 unterscheidet (kann links oder rechts von x sein).Planen Sie es
• Schritt 4: Zeichnen Sie eine Linie durch die Punkte (x0, f (x0)) und (x1, f (x1)).
• Schritt 5: Wählen Sie einen Punkt x2, der auf halber Strecke zwischen x0 und x1 liegt, und zeichnen Sie eine Linie durch die Punkte (x0, f (x0)) und (x2, f (x2)).
• Schritt 6: Wiederholen Sie diesen Vorgang einige Male

Diese grafische Methode hilft Ihnen dabei, eine grobe Vorstellung davon zu erhalten, wie die Tangentenlinie aussieht, ist jedoch eine Annäherung (es sei denn, die Funktion f (x) ist linear).

Tangentenlinienformel

Die Näherungsmethode mit Hilfe von Sekantenlinien kann Ihnen eine Vorstellung davon geben, wonach Sie suchen, aber glücklicherweise gibt es eine exakte Formel zur Berechnung der Tangente an eine Funktion in einem Punkt \(x_0\). Die Formel für die Tangente lautet:

\[\displaystyle y = f(x_0) + f'(x_0) (x - x_0) \]

Einfach, oder?In einfachen Worten zeigt diese Formel, dass die Tangentenlinie a ist Linie, Diedirch Den Punkt Geht \((x_0, f(x_0))\) und die eine Steigung von \(m = f'(x_0)\) hat

Die Steigung der Tangente an einem bestimmten Punkt ist also, einfach ausgedrückt, genau die Ableitung der Funktion an diesem Punkt.

Schritte zum anwenden der tangentenlinienformel

• Schritt 1: Identifizieren Sie die Funktion f (x) und den Punkt x0
• Schritt 2: Berechnen Sie den Wert der Funktion bei x0, dh f (x0)
• Schritt 3: Berechnen Sie die Ableitung von F (x) an Punkt X0, sodass Sie F '(x0) benötigen.
• Schritt 4: Direkte Anwendung der Formel für die Tangente \(y = f(x_0) + f'(x_0) (x - x_0)\)

Sobald Sie das haben Geilung der Linie Sie können es in das Format verwandeln, dass es für die jeweilige Situation am nützlichsten ist.

Die neigung der tangentenlinie

Eine der wichtigsten Erkenntnisse ist, dass die Steigung der Tangente an \(x_0\) genau \(f'(x_0)\) ist, was der Ableitung am Punkt \(x_0\) entspricht. Dies liefert eine klare und äußerst nützliche Interpretation der Ableitung in geometrischen Begriffen.

Diese Verbindung ermöglicht es, die Gleichung der Tangentenlinie zu einer bestimmten Kurve an einem bestimmten Punkt zu finden, indem einfach die Ableitung der Funktion betrachtet wird.

Wann haben sie eine horizontale tangente?

Eine horizontale Tangente entsteht, wenn der gewählte Punkt \(x_0\) die entsprechende Ableitung an diesem Punkt gleich Null ist. In diesem Fall verläuft die Tangente (d. h. die Linie, die die Kurve an einem Punkt lokal berührt) parallel zur y-Achse.

Alles, was man also wissen muss, um horizontale Tangenten zu erkennen, ist, Punkte zu finden, an denen die Ableitung der Funktion Null ist.

Wann haben sie eine vertikale tangente?

Eine vertikale Tangente liegt vor, wenn die Ableitung in einem Punkt "unendlich" ist. Dies ist eine einfache Art zu sagen, dass die Ableitung in einem bestimmten Punkt nicht definiert ist, aber bei Annäherung an den Punkt gegen unendlich konvergiert.

Zum Beispiel könnte man sagen, dass \(f(x) = \frac{1}{x}\) eine vertikale Tangente an x = 0 hat. Man könnte aber auch argumentieren, dass es keine Tangente gibt, weil die Ableitung bei x = 0 nicht wohldefiniert ist.

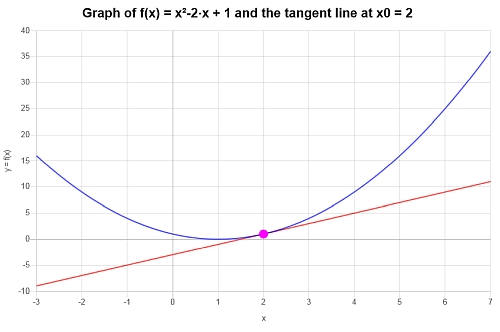
Beispiel: tangentenlinie

Ermitteln Sie die Gleichung der Tangente an \(f(x) = x^2 - 2x + 1\) im Punkt \(x_0 = 2\).

Lösung: Die folgende Funktion ist diejenige, mit der wir arbeiten müssen: \(\displaystyle f(x)=x^2-2x+1\). Zunächst müssen wir ihre Ableitung berechnen.

Die Funktion wurde bereits vereinfacht, sodass wir direkt sein Ableitungsbereich berechnen können:

Tangente : Die Gleichung der Tangente an die Funktion \(\displaystyle f(x)=x^2-2x+1\) im Punkt \(x_0 = 2\) lautet:

\[y = y_0 + f'(x_0)(x - x_0) \]

In diesem Fall ist es \(\displaystyle y_0 = f(x_0)\). Wenn man also den Wert des Punktes \(x_0 = 2\) in die Funktion einfügt, ergibt sich folgendes:

\[y_0 = f(x_0) = f(2) = 2^2-2\cdot 2+1 = 1 \]

Auch das Einsetzen des Wertes des Punktes \(x_0 = 2\) in die berechnete Ableitung führt zu:

\[f'(x_0) = f'(2) = 2\cdot 2-2 = 2 \]

Dann stecken wir diese Werte jetzt in die Tangentenlinienformel ein, um zu erhalten:

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 1+2\left(x-2\right) = 2x-3 \]

Schlussfolgerung : Daher wird festgestellt, dass die Tangente für die Funktion \(\displaystyle f(x)=x^2-2x+1\) im Punkt \(x_0 = 2\) ist:

\[y = 2x-3 \]

Die folgende Darstellung ergibt sich für die gegebene Funktion und ihre Tangente an \(x_0 = 2\):

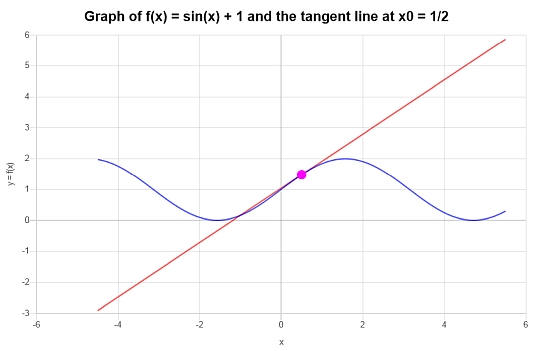
Beispiel: tangentenliniengleichung

Wie lautet die Tangente an x = 1/2 für die Funktion \(f(x) = \sin(x) + 1\)?

Lösung:

Die folgende Funktion wurde bereitgestellt: \(\displaystyle f(x)=\sin\left(x\right)+1\), für die wir ihre Ableitung berechnen müssen.

Die Funktion wurde bereits vereinfacht, sodass wir direkt sein Ableitungsbereich berechnen können:

Tangente : Die entsprechende Gleichung der Tangente im Punkt \(x_0 = \frac{1}{2}\) ist gegeben durch:

\[y = y_0 + f'(x_0)(x - x_0) \]

Aber in diesem speziellen Fall, \(\displaystyle y_0 = f(x_0)\), was bedeutet, dass wir den Wert des Punktes \(x_0 = \frac{1}{2}\) in die Funktion einfügen müssen, so dass wir erhalten:

\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \sin\left(\frac{1}{2}\right)+1\]

Wenn wir nun das Gleiche bei der Ableitung tun, finden wir für \(x_0 = \frac{1}{2}\)

\[f'(x_0) = f'\left(\frac{1}{2}\right) = \cos\left(\frac{1}{2}\right) \]

Jetzt müssen wir nur die Werte anschließen, also finden wir das

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = \sin\left(\frac{1}{2}\right)+1+\cos\left(\frac{1}{2}\right)\left(x-\frac{1}{2}\right) = x\cos\left(\frac{1}{2}\right)-\frac{1}{2}\cos\left(\frac{1}{2}\right)+\sin\left(\frac{1}{2}\right)+1 \]

Schlussfolgerung : Wir finden, dass die entsprechende Tangente, die wir suchen, im entsprechenden Punkt \(x_0 = \frac{1}{2}\) gegeben ist durch

\[y = x\cos\left(\frac{1}{2}\right)-\frac{1}{2}\cos\left(\frac{1}{2}\right)+\sin\left(\frac{1}{2}\right)+1 \]

Grafisch:

Beispiel: eine andere tangentenlinie

Wie lautet die Tangente an x = 0 für die Funktion \(f(x) = \cos(x)\)? Ergibt dieses Ergebnis einen Sinn?

Lösung: Beachten Sie, dass \(f'(x) = -\sin(x)\), also dann \(f'(0) = -\sin(0) = 0\). Das heißt, die Tangente hat eine Steigung von m = 0 bei x = 0, also ist die Gleichung der Tangente einfach \(y = y_0 = \cos(0) = 1\). Das macht Sinn, denn in diesem Fall ist die Tangente eine horizontale Linie.

Weitere differenzierungsrechner

Einige Menschen können behaupten, dass die Differenzierung eine relativ einfache Übung ist und dass ein verwendet wird Derivatnetisch kann nicht benötigt werden, aber in Wahrheit kann die Berechnung von Derivaten immer noch ziemlich umständlich sein und möglicherweise langwierig erfordern Algebrasche Berechnungen .

Wenn Sie einen Ausdruck mit mehr als einer Variablen haben, müssen Sie feststellen, ob die Variablen voneinander unabhängig sind, um die Ableitung zu finden. In diesem Fall verwenden Sie in diesem Fall Telableitungen , oder wenn es eine Gleichung gibt, die die Variablen verknüpft. In diesem Fall müssten Sie verwenden Implizit -Unterschied .

Die beiden Hauptbereiche im Differentialkalkül sind Integration und Differenzierung, und beide haben überall ihre breiten Anwendungen. Telableitungen erscheinen in großer Länge in technischen und wirtschaftlichen Anwendungen.

Einerseits befasst sich die Differenzierung mit den unendlichen Veränderungsraten, während die Integration mit der Summierung infinitesimaler Veränderungsraten befasst ist, und dies sind dies bewundernswert, wenn sie eng von der verknüpft sind Grundsatz des Kalköls .