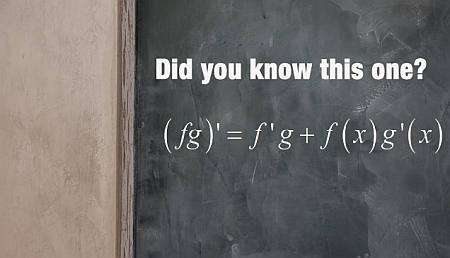Mehr über die produktregel
Dieser Taschenrechner hilft Ihnen dabei, die Ableitung von Funktionen mithilfe der Produktregel zu finden.Um den Taschenrechner zu verwenden, müssen Sie eine gültige Funktion bereitstellen, für die ein Produkt beteiligt ist.
Ein Beispiel für eine gültige Funktion könnte so etwas wie f (x) = x*sin (x) oder so etwas wie g (x) = sin (x)*cos (x), nur um nur einige zu erwähnen.
Dann tippen wir Dong die Funktion, für die Sie die Produktregel verwenden möchten. Sie müssen dann klicken. Sie müssen lediglich auf die Schaltfläche "Berechnen" klicken, und alle Schritte der Berechnungen werden bereitgestelltfür dich.
Eine der ersten Regelregel, die Sie lernen werden, ist in der Tat die Produktregel, da die meisten Funktionen, die Sie aus elementaren Funktionen konstruieren, das Produkt von Funktionen verwenden.

Produktregelformel
Lernen über
Derivatregel
ist vielleicht das erste, was Sie tun werden, wenn Sie lernen, wie es geht
Funde sie Dasivat
einer Funktion.Und eins ist die erste Regeln, die Sie lernen werden, ohne Zweifel die Produktregel.
Die Produktregel einfach ist eine Regel, die Ihnen hilft, die Ableitung eines Produkts von Funktionen zu berechnen.Die Produktregelformel lautet:
\[\displaystyle (f(x) g(x))' = f'(x) g(x) + f(x) g'(x) \]
Schritte zur verwendung der produktregel
-
Schritt 1:
Identifizieren Sie klar die Funktionen F (x) und g (x), die das Produkt bilden, mit dem Sie arbeiten
-
Schritt 2:
Bei Bedarf Vereinfachungen vereinfachen, während die Produktstruktur beibehalten wird
-
Schritt 3:
Verwenden Sie die Produktregelformel: \((f(x) g(x))' = f'(x) g(x) + f(x) g'(x) \), bei der der Wert der Funktionen f (x) und g (x) sowie der Derivate f '(x) und g' (x) angeschlossen werden soll.
Durch die Arbeit mit einem Produktregelderivat erhalten Sie im Wesentlichen die Ableitung des Produkts auf der Grundlage der Kenntnis der individuellen Funktionen und ihrer Derivate.
Welche anderen ableitungen gibt es?
Abgesehen von der Produktregel gibt es andere wichtige Regeln wie die Linearitätsregel, die
Quotienteregel
was besagt, dass \(\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}\) und die
Kettenregel
, was sagt, dass \(\frac{d}{dx} f(g(x)) = f'(g(x))g'(x)\).
Sie werden auch andere Regeln finden, die um die Leistungsregel erwähnt werden, die angibt, dass \(\frac{d}{dx} x^n = n x^{n-1}\) für eine konstante \(n\).

Tipps und tricks
Die Produktregel kann als abgeleitete Multiplikationsregel betrachtet werden, und die Produktregel spielt eine entscheidende Rolle im Kalkül, sodass sie sich auszahlt, um sie gut zu lernen.
Beachten Sie, dass Sie bei multivariablen Funktionen die Regel der Matrixmultiplikation verwenden können, um die Produktregel zu betreiben.
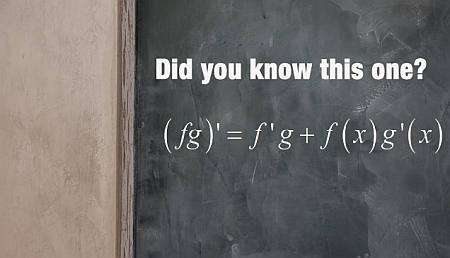
Beispiel: verwenden der produktregel
Berechnen Sie die Ableitung von: \(f(x) = (x-1)(2x+1) \)
Lösung:
Wir betrachten die folgende Funktion \(\displaystyle f(x)=\left(x-1\right)\left(2x+1\right)\), die differenziert werden muss.
\( \displaystyle \frac{d}{dx}\left(\left(2x+1\right)\left(x-1\right)\right)\)
By using the Product Rule: \(\frac{d}{dx}\left( \left(2x+1\right)\left(x-1\right) \right) = \frac{d}{dx}\left(2x+1\right) \cdot \left(x-1\right)+\left(2x+1 \right) \cdot \frac{d}{dx}\left(x-1\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(2x+1\right) \cdot \left(x-1\right)+\left(2x+1 \right) \cdot \frac{d}{dx}\left(x-1\right)\)
By linearity, we know \(\frac{d}{dx}\left( x-1 \right) = \frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\) and \(\frac{d}{dx}\left( 2x+1 \right) = \frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:
\( \displaystyle = \,\,\)
\(\displaystyle \left(\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)\right) \left(x-1\right)+\left(2x+1 \right) \left(\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\right)\)
Since the derivative of a constant is 0, we find that:
\( \displaystyle = \,\,\)
\(\displaystyle \left(\frac{d}{dx}\left(2x\right)\right) \left(x-1\right)+\left(2x+1 \right) \left(\frac{d}{dx}\left(x\right)\right)\)
It is known that \(\frac{d}{dx}\left(x\right) = 1\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(\frac{d}{dx}\left(2x\right)\right) \left(x-1\right)+\left(2x+1 \right)\)
So, we directly get: \(\frac{d}{dx}\left( 2x \right) = 2\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(2\right) \left(x-1\right)+\left(2x+1 \right)\)
\( \displaystyle = \,\,\)
\(\displaystyle 2x+1+2\left(x-1\right)\)
Note that \((2) \cdot (x-1) = 2x-2\cdot 1 = 2x-2\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right
\( \displaystyle = \,\,\)
\(\displaystyle 2x+1+2x-2\)
Grouping the terms with \(x\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(2+2\right)x+1-2\)
Grouping together numerical values and operating the terms that were grouped with \(x\)
\( \displaystyle = \,\,\)
\(\displaystyle 4x+1-2\)
Reducing the integers that can be subtracted together: \(\displaystyle 1-2 = -1\)
\( \displaystyle = \,\,\)
\(\displaystyle 4x-1\)
Fazit
: Daher wird der Schluss gezogen, dass die Ableitung der Funktion lautet:
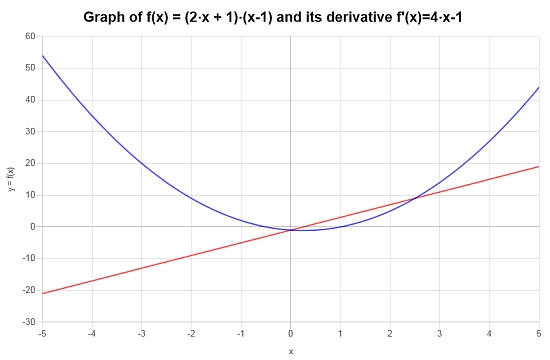
\[f'(x) = 4x-1\]
Grafisch zeigt das folgende Diagramm die Situation:
Beispiele für produktregel
Finden Sie die Ableitung von: \(f(x) = x \sin(x)\)
Lösung:
In diesem Beispiel lautet die angegebene Funktion \(\displaystyle f(x)=x\sin\left(x\right)\).Lassen Sie uns sein Derivat finden
\( \displaystyle \frac{d}{dx}\left(x\sin\left(x\right)\right)\)
Wir verwenden die Produktregel: \(\frac{d}{dx}\left( x\sin\left(x\right) \right) = \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)\)
Indem wir direkt unterscheiden, finden wir: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \cos\left(x\right)\)
Nach der Vereinfachung bekommen wir das:
\( \displaystyle = \,\,\)
\(\displaystyle x\cos\left(x\right)+\sin\left(x\right)\)
Fazit
: DAHER STELLEN WIR FEST, DASS DIELELTUNG DURCH DIE FOLGENDE Formel Angegeben ist:
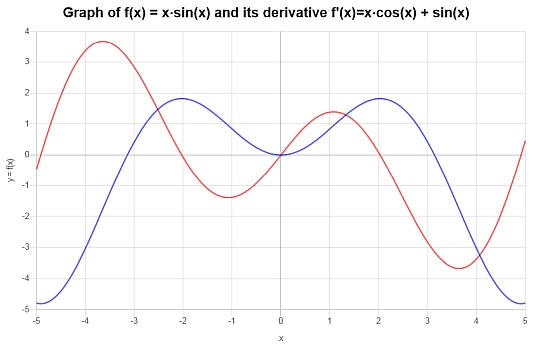
\[f'(x) = x\cos\left(x\right)+\sin\left(x\right)\]
Das Folgende Diagramm ist für Funktion und iHr ferleitung konstruiert:
Beenpiel: eine andere berechnung der produktregel
Unersche an der Folgende Funktion \( f(x) = x (x+1)^2 \).
Lösung:
Schliebenlich Lautet Die Angegebe Funktion in Dieem BEISPIEL \(\displaystyle f(x)=x\left(x+1\right)^2\).
\( \displaystyle \frac{d}{dx}\left(\left(x+1\right)^2x\right)\)
Wir verwenden die Produktregel: \(\frac{d}{dx}\left( \left(x+1\right)^2x \right) = \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 \cdot \frac{d}{dx}\left(x\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 \cdot \frac{d}{dx}\left(x\right)\)
Wir wissen, dass \(\frac{d}{dx}\left(x\right) = 1\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 \)
Verwenden der Leistungsregel für einen konstanten Exponenten: \(\frac{d}{dx}\left( \left(x+1\right)^2 \right) = 2x+1\cdot \frac{d}{dx}\left(x+1\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(2x+1\cdot \frac{d}{dx}\left(x+1\right)\right) x+\left(x+1\right)^2 \)
Nach Linearität wissen wir \(\frac{d}{dx}\left( x+1 \right) = \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)\), also stecken Sie das in:
\( \displaystyle = \,\,\)
\(\displaystyle \left(2x+1\left(\frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)\right)\right) x+\left(x+1\right)^2 \)
Die Ableitung einer Konstante beträgt 0, also:
\( \displaystyle = \,\,\)
\(\displaystyle \left(2x+1\left(\frac{d}{dx}\left(x\right)\right)\right) x+\left(x+1\right)^2 \)
Wir wissen, dass \(\frac{d}{dx}\left(x\right) = 1\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(2x+1\right) x+\left(x+1\right)^2 \)
\( \displaystyle = \,\,\)
\(\displaystyle \left(x+1\right)^2+2\left(x+1\right)x\)
Erweiterung der Begriffe: \(\left(x+1\right)^2 = \left(x+1\right)\left(x+1\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(x+1\right)\left(x+1\right)+2\left(x+1\right)x\)
Beachten Sie, dass \((x+1) \cdot (x+1) = x^2+1x+1x+1^2 = x^2+2x+1\), da wir die Verteilungseigenschaft für jeden Begriff des Ausdrucks links in Bezug auf die Begriffe auf der rechten Seite verwenden können
\( \displaystyle = \,\,\)
\(\displaystyle x^2+2x+1+2\left(x+1\right)x\)
Beachten Sie, dass \((x+1) \cdot (x) = x^2+1x = x^2+x\) aufgrund der Tatsache, dass wir die Verteilungseigenschaft für jeden Term des Ausdrucks links in Bezug auf die Begriffe rechts verwenden können
\( \displaystyle = \,\,\)
\(\displaystyle x^2+2x+1+2\left(x^2+x\right)\)
Wir erhalten \((2) \cdot (x^2+x) = 2x^2+2x = 2x^2+2x\), indem wir die Verteilungseigenschaft für jeden Begriff des Ausdrucks links in Bezug auf die Begriffe auf der rechten Seite verwenden
\( \displaystyle = \,\,\)
\(\displaystyle x^2+2x+1+2x^2+2x\)
Gruppieren Sie die Begriffe mit \(x\), \(x^2\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(2+2\right)x+\left(1+2\right)x^2+1\)
Die Ganzzahlen zusammenfügen und die Begriffe vereinfachen, die mit \(x\), \(x^2\) gruppiert wurden
\( \displaystyle = \,\,\)
\(\displaystyle 4x+3x^2+1\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(3x+1\right)\left(x+1\right)\)
Fazit
: Basierend auf Dem, war beobe berechnet wurde, wird festgestell, Dasivspeivat Derivat Lautet:
\[f'(x) = \left(3x+1\right)\left(x+1\right)\]
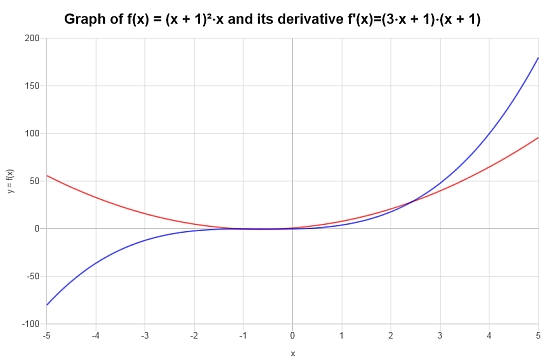
Das Folgende Diagramm Wird für Die Angegebe Funktion Auf dem -intervall \([-5, 5]\) Erhalten:
Mehratrechtner
Nur Wenige Menschen Werden Dieser Differenzierung Zusammen MIT Integration und Zentralem Kalkül Nick Zustimmen.
Berechnung Eines Derivat
ist ein Inentscheidende fähigkeit, Die Sie als Kalköl -Student Lernen Müssen.
Sie Kön Können Imper
Teildifferenzierung
Ebenso Gut Wie
Implizit -Unterschied
, sterben in Verschiedenen Anwendungskontexten Verwendet Werden.
Anwendungen Umfassen
Tangente
Berechnung, Die Gleiich ist Wie a
Lineare Nähung
Sowie Die Verwendung von Derivaten Höherer Ordnung, Annend MIT
Derivat Zweiiter Ordnung
.