Löser Infinitesimalrechnung

Ableitungsregeln

Anweisungen: Verwenden Sie diesen Ableitungsrechner, um die Ableitung jeder von Ihnen bereitgestellten Funktion mit den häufigsten Ableitungen zu ermitteln, die alle Schritte angezeigt.Bitte geben Sie die Funktion ein, die Sie abgeleitet möchten, in dem folgenden Formularfeld.

Über abgeleitete regeln

Mit diesem Taschenrechner können Sie die Ableitung einer Funktion berechnen, die Sie anwenden, indem Sie die erforderlichen grundlegenden Differenzierungsregeln anwenden, alle Schritte des Prozesses zeigen und feststellen, wo jede Regel angewendet wird.

Sie müssen nur eine gültige Funktion bereitstellen, die differenzierbar ist (was bedeutet, dass sie ein Derivat hat).Beispielsweise könnte eine gültige Funktion f (x) = 1/3*x*sin (x) sein, um nur ein Beispiel zu erwähnen.

Wenn Sie Ihre Funktion bereits eingegeben haben, klicken Sie einfach auf "Berechnen", um alle Schritte der angezeigten Differenzierung zu erhalten.

Die Einfachheit der Regeln der Derivate macht den Differenzierungsprozess zu einem, der als „einfach“ anerkannt wird, ein Urteil, das möglicherweise eine Überbeanspruchung ist.

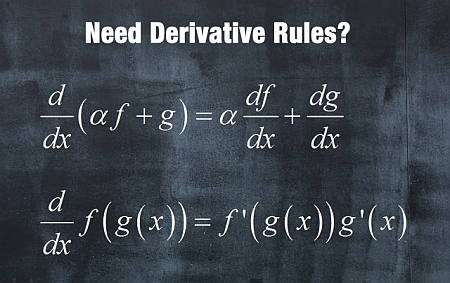
Grundlegende ableitungsregeln

Es gibt vier grundlegende Ableitungsregeln, die Sie lernen können

Linearitätsregel: Für Funktionen \(f(x)\) und \(g(x)\) und eine konstante \(a\) ist das Ableitungsableitungsvorgang eine lineare Operation: \((af(x)+g(x))' = af'(x)+g'(x)\)
Produktregel Für Funktionen \(f(x)\) und \(g(x)\) ist die Ableitung des Produkts \((f(x)g(x))' = f'(x)g(x) + f(x)g'(x)\)
Quotienteregel: Für Funktionen \(f(x)\) und \(g(x)\) ist die Ableitung des Quotienten \(\left(\frac{f(x)}{g(x)}\right)' = \left(\frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)}\right)\)
Kettenregel Für Funktionen \(f(x)\) und \(g(x)\) ist die Ableitung der zusammengesetzten Funktion \((f(g(x)))' = f'(g(x))g'(x)\)

Diese Regeln funktionieren wie ein Charme und helfen Ihnen, die Ableitung jeder grundlegenden Funktion zu finden.

Wie benutze ich die ableitungsregeln?

Schritt 1: Identifizieren Sie die Funktion f (x), die Sie unterscheiden möchten, und vereinfachen Sie bei Bedarf
Schritt 2: Versuchen Sie, die Funktion unter Verwendung der Linearität in kleinere abgeleitete Stücke zu unterteilen
Schritt 3: Verwenden Sie abhängig von der Struktur der Funktion F (x) die verfügbaren Regeln (Produkt-, Quoten- und Kettenregel) und sind Sie sich bewusst, dass Sie möglicherweise viele der Regeln nacheinander anwenden müssen).

Normalerweise werden Sie eine Kombination aus mehreren Differenzierungsregeln erhalten, bis Sie Punkte erreichen, an dem Sie eine elementare Funktion finden, von der Sie bereits wissen, wie Sie es unterscheiden können.

Kann ich alle derivate lösen?

Wenn Sie sagen, dass Sie mit Differenzierungsregeln alle Derivate verwenden können, kann dies eine Überbeamte sein.Sie werden in der Lage sein, die meisten und sicherlich alle grundlegenden Derivate zu lösen, aber es gibt Funktionen, die ein weniger intuitives Verhalten haben, das definiert werden kann, obwohl sie in den grundlegenden Kalkülkursen in der Regel nicht behandelt werden.

Für welche grundlegenden Funktionen werden die meisten von ihnen ohne Problem unterschieden.

Ein Produktregel Derivat Anwesend Quotienteregel Derivat oder Kettenregelderivat Es ist unwahrscheinlich, dass es isoliert ist, und wird wahrscheinlich in einer Abfolge mehrerer Regeln kommen, die zusammen verwendet werden müssen.

Beispiel: ableitungsregeln

Berechnen Sie die folgende Ableitung anhand der grundlegenden Ableitungen: \(\frac{d}{dx}\left( x^2 \cos(x^2) \right)\)

Lösung: Betrachten wir die folgende angegebene Funktion, für die das Ableitungen berechnet werden muss \(\displaystyle f(x)=x^2\cos\left(x^2\right)\)

Die Funktion erfordert keine Vereinfachung, sodass wir direkt in die Berechnung ihres Ableitung eingehen können:

\( \displaystyle \frac{d}{dx}\left(x^2\cos\left(x^2\right)\right)\)

Now, using the Product Rule: \(\frac{d}{dx}\left( x^2\cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)\)

We have to use the Chain Rule: \(\frac{d}{dx}\left( \cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right)\cdot \left(-\sin\left(x^2\right)\right)\) and using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(2x\right) \cos\left(x^2\right)+x^2 \cdot 2x\cdot \left(-\sin\left(x^2\right)\right)\)

so then we get

\( \displaystyle = \,\,\)

\(\displaystyle x^2\cdot 2x\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)\)

By reordering some of the numerical values, and then grouping the terms with \(x\) in the term \(x^2\cdot 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x^3\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)\)

But we get \((2x^3) \cdot (-\sin\left(x^2\right)) = -2x^3\sin\left(x^2\right) = -2x^3\sin\left(x^2\right)\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle -2x^3\sin\left(x^2\right)+2x\cos\left(x^2\right)\)

And finally, grouping the terms together

\( \displaystyle = \,\,\)

\(\displaystyle -2\left(x^2\sin\left(x^2\right)-\cos\left(x^2\right)\right)x\)

Das entsprechende Diagramm der Funktion und ihre Ableitung ist unten dargestellt:

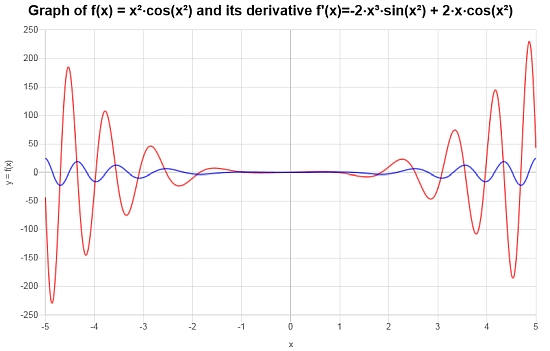
Beispiel: mehr abgeleitete regeln

Berechnen Sie die folgende Ableitung: \(\frac{d}{dx}\left( x \cos(x^2+1) \right)\) Verwenden der grundlegenden Ableitungsregeln.

Lösung: Jetzt besteht die vorliegende Aufgabe darin, die Funktion \(\displaystyle f(x)=x\cos\left(x^2+1\right)\) zu differenzieren

\( \displaystyle \frac{d}{dx}\left(x\cos\left(x^2+1\right)\right)\)

In this case, we have to use the Product Rule: \(\frac{d}{dx}\left( x\cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)\)

The Chain Rule for this composition: \(\frac{d}{dx}\left( \cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^2+1 \right) = \frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(2x\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)

which then leads to

\( \displaystyle = \,\,\)

\(\displaystyle x\cdot 2x\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)\)

Putting together the numerical values and grouping the terms with \(x\) in the term \(x\cdot 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x^2\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)\)

Observe that \((2x^2) \cdot (-\sin\left(x^2+1\right)) = -2x^2\sin\left(x^2+1\right) = -2x^2\sin\left(x^2+1\right)\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle -2x^2\sin\left(x^2+1\right)+\cos\left(x^2+1\right)\)

So then we get

\( \displaystyle = \,\,\)

\(\displaystyle -2x^2\cos\left(x^2\right)\sin\left(1\right)-2x^2\cos\left(1\right)\sin\left(x^2\right)+\cos\left(1\right)\cdot \cos\left(x^2\right)-\sin\left(1\right)\cdot \sin\left(x^2\right)\)

Beispiel für abgeleitete regeln

Verwenden Sie für die Funktion \( f(x) = (x-1)(x^2+1) \) die Ableitungsregeln, um ihre Ableitung zu finden.

Lösung: Für dieses letzte Beispiel müssen wir: \(\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)\) differenzieren.

Erstschritt: In diesem Fall müssen wir zunächst die angegebene Funktion \(\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right) \) erweitern, und dazu führen wir die folgenden Vereinfachungsschritte durch:

\( \displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)\)

Note that \((x-1) \cdot (x^2+1) = x\cdot x^2+x-x^2-1^2 = x^3-x^2+x-1\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle x^3-x^2+x-1\)

Nach der Erweiterung der Funktion können wir mit der Berechnung des Derivats fortfahren:

\( \displaystyle \frac{d}{dx}\left(x^3-x^2+x-1\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^3-x^2+x-1 \right) = \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\)

The derivative of a constant is 0, so then:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)\)

We know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+1\)

Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\) and \(\frac{d}{dx}\left( x^3 \right) = 3x^2\)

\( \displaystyle = \,\,\)

\(\displaystyle 3x^2-2x+1\)

Grafisch ist so die Funktion und ihr abgeleitete Aussehen:

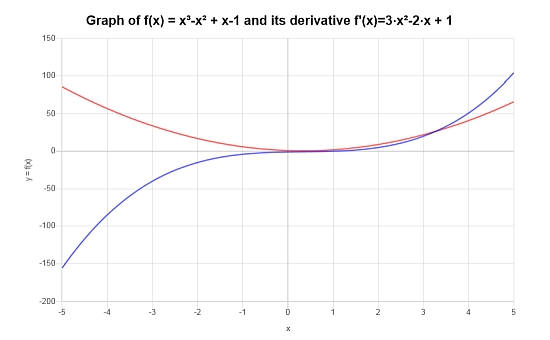
Mehr derivatrechner

Eine der Magie über Differenzierung ist, dass Sie können Funde sie Dasivat von jeder Funktion unter Verwendung einiger grundlegender und einfacher Regeln, einschließlich der Produktregel Anwesend Quotienteregel und natürlich, Die Kettenregel .Dieses kleine Arsenal reicht in der Regel aus, um ein Derivat zu berechnen, das Sie benötigen

Differenzierung und Integration sind die Hauptspuren im Kalkül ohne Streit, da sie das Zentrum so vieler Anwendungen in allen Aspekten der Wissenschaft sind.Von verwandten Preisen bis Implizit -Unterschied , mit Telableitungen in Physik und Wirtschaftlichkeit