Löser Infinitesimalrechnung

Implizite differenzierungsrechner

Anweisungen: Verwenden Sie diesen Rechner für implizite Differenzierung, um die Ableitung \(\frac{dy}{dx}\) zu berechnen, wenn \(x\) und \(y\) über eine Gleichung verbunden sind. Geben Sie eine Gleichung, die x und y beinhaltet, in das untenstehende Formularfeld ein.

Implizite differenzierung

Dieser Taschenrechner hilft Ihnen dabei, eine implizite Differenzierung für eine Gleichung durchzuführen, die die Variablen x und y betrifft.Sie müssen eine gültige Gleichung wie x^2 + y^2 = 1 oder xy - x^2 y^2 = 0 usw. angeben.

Sobald Sie eine gültige Gleichung mit zwei Variablen (\(x\) und \(y\)) angeben, müssen Sie nur noch auf die Schaltfläche "Berechnen" klicken, und alle Schritte der entsprechenden impliziten Differenzierung werden angezeigt.

Dies ist eine dy/dx-Rechner mit Stufen in dem Sinne, dass es Ihnen alle relevanten Schritte der Berechnung der Ableitung einer Variablen nach einer anderen aufzeigt, sofern diese beiden Variablen in einer Gleichung miteinander verbunden sind. Diese Beziehung ermöglicht es Ihnen, die entsprechende Ableitung zu finden implizite Ableitung .

Wenn wir eine Gleichung haben, die die beiden Variablen \(x\) und \(y\) in Beziehung setzt, sollten wir in der Lage sein, \(y\) als Funktion von \(x\) auszudrücken und \(y = y(x)\) zu schreiben. Oft können wir \(y\) nicht explizit als Funktion von \(x\) ausdrücken, sondern nehmen an, dass es eine solche Funktion gibt. In diesem Fall ist es sinnvoll, \(y\) nach \(x\) zu differenzieren.

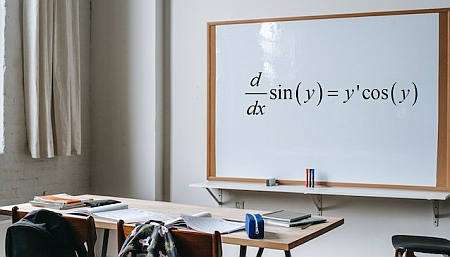
Was ist implizite differenzierung?

Implizite Differenzierung ist eine differenzierungsrechnung technik, die auf der Annahme beruht, dass es möglich ist, aus einer gegebenen Gleichung mit \(x\) und \(y\) zu schließen, dass \(y\) eine Funktion von \(x\) ist, obwohl wir diese Funktion oft nicht explizit schreiben können.

Sobald diese Annahme getroffen ist, gehen wir davon aus, dass wir \(\frac{dy}{dx}\) berechnen können und wir alle bekannten Fähigkeitsregeln ( Produktregel , Quotienteregel und Kettenregel ), um beide Seiten der Gleichung zu differenzieren, und lösen Sie für \(\frac{dy}{dx}\).

Was ist die implizite differenzierungsmethode?

Die implizite Differenzierungsmethode ist eine Methode, die es Ihnen ermöglicht, eine Ableitung von Ausdrücken zu berechnen, die nicht direkt im Format \(f(x)\) angegeben sind. Das heißt, wenn wir zum Beispiel eine Funktion einer Variablen \(x\) gegeben haben, machen wir einfach weiter und differenzieren diese Funktion.

Wenn aber zwei Variablen \(x\) und \(y\) über eine Gleichung miteinander verbunden sind, wie z.B. \(x^2+y^2 = 1\), kann man auch y nach x differenzieren. Nach der traditionellen Methode muss man y in Bezug auf x lösen und DANN kann man differenzieren.

Mit der impliziten Differenzierung können Sie direkt differenzieren, indem Sie nur die Annahme machen, dass \(y = y(x\), und die Verwendung der Kettenregel .

Schritte zur verwendung implizite differenzierung

Schritt 1: Identifizieren Sie die Gleichung, die zwei Variablen x und y umfasst.Vereinfachen Sie alle redundanten Begriffe
Schritt 2: Angenommen, y ist eine Funktion von x, y = y (x), daher ist es sinnvoll, die Ableitung von y in Bezug auf x zu berechnen
Schritt 3: Berechnen sie Dasivat von beiden Seiten der Gleichung unter Verwendung aller Fähigkeitsregeln du brauchst.Dies wird zu einer Gleichheit führen, in der x, y und y möglicherweise vorhanden sind
Schritt 4: Lösen Sie, was Sie in Schritt 3 für y erhalten haben.Beachten Sie, dass y 'normalerweise als Funktion von x und y geschrieben wird, was in Ordnung ist, da y auch von x abhängt

Dies ist eine sehr allgemeine Methodik, und es wird Feinheiten von Fall zu Fall haben, aber das ist die Blaupause, die in den meisten Fällen funktionieren sollte, wobei die zusätzlichen potenziellen algebraischen Manipulationen Schwierigkeiten haben.

Warum unter verwendung eines impliziten differenzierungsrechners

Die implizite Differenzierung könnte manchmal verwirrend sein, wenn Sie nicht sehr klar sind, was Sie unterscheiden und welche Variable.Ein Taschenrechner hilft Ihnen dabei, Ihr Ergebnis zu vergleichen, und eine besondere Sache an unserem Taschenrechner ist, dass alle Schritte des Prozesses angezeigt werden.

Das ist eine entscheidende Hilfe für Sie, da es Ihnen genau zeigt, welche derivativen Regel und wo Sie sie angewendet haben.

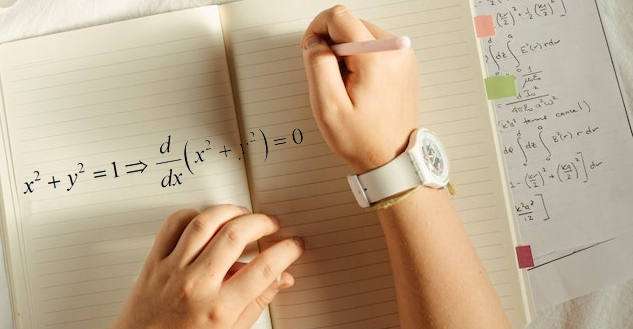
Was ist der sinn der implizite differenzierung?

Das ist eine faire Frage.Wenn Sie eine Gleichung mit x und y haben, warum nicht y in Bezug auf x und verwenden Sie eine regelmäßige Ableitungsberechnung, um die Ableitung von y in Bezug auf x zu erhalten.Ich kann Ihnen mindestens zwei gute Gründe geben:

Grund 1: Es kann sein, dass Sie y in Bezug auf X explizit nicht lösen können.Es kann eine Funktion geben, aber Sie können sie nicht einfach finden.Denken Sie an y + tan (y) = x^2
Grund 2: Auch wenn Sie zufällig Lösen Sie y in Deraufzeit von x Es kann ein wirklich komplizierter Ausdruck sein, und die abgeleitete Berechnung könnte sehr verworren und schwierig sein.Normalerweise ist die implizite Differenzierung algebraisch einfach in relativ

Hängt das implizite derivat von y ab?

Nicht immer, aber oft. Damit wird nur gesagt, dass \(\frac{dy}{dx}\) von x und y abhängen kann, aber da y von x abhängt, heißt es nur, dass \(\frac{dy}{dx}\) erwartungsgemäß von x abhängt.

Im folgenden Abschnitt werden unterschiedliche Beispiele für implizite Differenzierung vorgestellt.

Zweite implizite ableitung

Eine Frage ist: Kann man die zweite Ableitung mit impliziter Differenzierung berechnen? Die Antwort ist JA. Man macht einfach dasselbe wie bei der ersten Ableitung mit impliziter Differenzierung, man nimmt einfach an, dass \(y\) eine Funktion von \(x\) ist, also schreibt man \(y = y(x)\), und man kann so viel differenzieren, wie man will.

Ein Beispiel: Sie wollen \(\frac{d^2y}{dx^2}\) finden, wenn Sie die Gleichung \(x^2+y^2=1\) haben. Differenzieren Sie beide Seiten in Bezug auf \(x\):

\[ \frac{d}{dx}\left(x^2+y^2\right)=\frac{d}{dx}\left(1\right)\] \[ \Rightarrow 2x+2yy' = 0\]

Nun differenzieren Sie wieder nach x:

\[ \frac{d}{dx}\left(2x+2yy'\right)=\frac{d}{dx}\left(0\right)\] \[ \Rightarrow 2+2(y')^2+2yy'' = 0\]

und jetzt lösen wir für \(y''\):

\[ \Rightarrow y'' = -\frac{(2+2(y')^2)}{2y}\] \[ \Rightarrow y'' = -\frac{(1+(y')^2)}{y}\]

Beispiel: beispiel für implizite differenzierung

Finden Sie \(\frac{dy}{dx}\) für die Gleichung: \(x^2 - y^2 = 2y\)

Lösung: Dies ist ein Beispiel für implizite Differenzierung. Die folgende Gleichung ist gegeben: \(\displaystyle x^2-y^2=2y\), für die wir eine implizite Differenzierung durchführen müssen, wobei wir annehmen, dass \(y\) eine Funktion von \(x\) ist.

Die Gleichung erfordert keine weitere Vereinfachung, sodass wir mit der impliziten Differenzierung fortfahren können:

Wir müssen beide Seiten der Gleichung in Bezug auf \(x\) differenzieren, und auf beiden Seiten nehmen wir an, dass \(y = y(x)\).

Linke Site : Differenzierung der linken Seite in Bezug auf \(x\)

\( \displaystyle \frac{d}{dx}\left(x^2-y^2\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^2-y^2 \right) = \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(y^2\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(y^2\right)\)

Using the Chain Rule: \(\frac{d}{dx}\left( y^2 \right) = 2y\cdot \frac{d}{dx}\left(y\right)\) and using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x-2y\cdot \frac{d}{dx}\left(y\right)\)

We assume that \(y\) is a function of \(x\): \(\frac{d}{dx}\left( y \right) = \frac{dy}{dx}\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x-2y\cdot \frac{dy}{dx}\)

Sete Sete : Differenzierung der rechten Seite in Bezug auf \(x\)

\( \displaystyle \frac{d}{dx}\left(2y\right)\)

Since it is a constant times \(y\), we directly get: \(\frac{d}{dx}\left( 2y \right) = 2 \cdot \frac{d}{dx}\left(y\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle 2 \cdot \frac{d}{dx}\left(y\right)\)

We assume that \(y\) is a function of \(x\): \(\frac{d}{dx}\left( y \right) = \frac{dy}{dx}\)

\( \displaystyle = \,\,\)

\(\displaystyle 2 \cdot \frac{dy}{dx}\)

Nach Differenzierung beider Seiten in Bezug auf \(x\) ergibt sich daher Folgendes:

\[\displaystyle 2x-2y\frac{dy}{dx} = 2\frac{dy}{dx}\]

Setzen Sie alle Begriffe auf eine Seite:

\[-2\,y\frac{d}{dx}y+2\,x-2\,\frac{d}{dx}y = 0\]

Gruppierung von allem, was \(\displaystyle \frac{dy}{dx}\) enthält:

\[-2\,{\left(y+1\right)}\frac{d}{dx}y+2\,x = 0\]

Schließlich führt die Lösung für \(\displaystyle \frac{dy}{dx}\) zu:

\[\displaystyle \frac{dy}{dx} = \frac{x}{y+1}\]

Beispiel: implizite differenzierungsberechnungen

Was ist die Steigung der Tangente an einen Einheitskreis im Punkt \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\)?

Lösung: Beachten Sie, dass die Gleichung des Einheitskreises \(\displaystyle x^2 + y^2 = 1\) ist, die implizit \(y\) als Funktion von \(x\) definiert. Um die Tangente zu finden, müssen wir \(\frac{dy}{dx}\) im angegebenen Punkt berechnen. Durch implizite Differenzierung differenzieren wir beide Seiten der Gleichung, die den Einheitskreis definiert: \[\displaystyle x^2 + y^2 = 1\] \[\Rightarrow \displaystyle \frac{d}{dx}\left(x^2 + y^2\right) = \frac{d}{dx}\left(1\right)\] \[\Rightarrow \displaystyle 2x+2yy' = 0 \] \[\Rightarrow \displaystyle 2yy' = -2x \] \[\Rightarrow \displaystyle y' = -\frac{x}{y} \]

Der Punkt von Interesse ist \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\), also .

#XYZA

Dies bedeutet, dass die Steigung der Tangente am Punkt \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\) \(m = -1\) ist, was bedeutet, dass die Gleichung der Tangente an diesem Punkt lautet

\[\displaystyle y - \frac{\sqrt{2}}{2} = -\left(x-\frac{\sqrt{2}}{2}\right)\] \[\Rightarrow \displaystyle y = \frac{\sqrt{2}}{2} - x + \frac{\sqrt{2}}{2}\] \[\Rightarrow \displaystyle y = \sqrt{2} - x \]

Beisiziel für die implizit -unterschiede

Betrachten Sie die Gleichung: \( \displaystyle \frac{2}{3} x + y^2 = \frac{2}{5} \). Berechne \(\frac{dy}{dx}\)

Lösung: In diesem Fall haben wir die folgende Gleichung: \(\displaystyle \frac{2}{3} x + y^2 = \frac{2}{5}\), also müssen wir eine implizite Differenzierung durchführen, unter der Annahme, dass \(y\) von \(x\) abhängt.

Ein weitere vereinfachung der gleichung ist nick erforderlich.DAHER KRNNEN WIR DANN MIT Der Impliziten Differzierung Fortfahre:

Nun müssen wir die Ableitung beider Seiten nach der Variablen \(x\) berechnen, wobei wir davon ausgehen, dass \(y = y(x)\).

Linke Site : Differenzieren der linken Seite in Bezug auf die Variable \(x\)

#XYZA

Mit Hilfe der Linearität kennen wir \(\frac{d}{dx}\left( \frac{2}{3}x+y^2 \right) = \frac{d}{dx}\left(\frac{2}{3}x\right)+\frac{d}{dx}\left(y^2\right)\), also setzen wir das ein:

#XYZA

Wir müssen die Kettenregel anwenden: \(\frac{d}{dx}\left( y^2 \right) = 2y\cdot \frac{d}{dx}\left(y\right)\) und wir erhalten direkt: \(\frac{d}{dx}\left( \frac{2}{3}x \right) = \frac{2}{3}\)

#XYZA

Angenommen, dass \(y\) eine Funktion von \(x\) ist: \(\frac{d}{dx}\left( y \right) = \frac{dy}{dx}\)

#XYZA

Sete Sete : Nun differenzieren wir die rechte Seite in Bezug auf \(x\)

#XYZA

Der Ausdruck ist eine Konstante, daher ist seine Ableitung 0

#XYZA

Das Ergebnis nach der Differenzierung beider Seiten in Bezug auf \(x\) ist also:

#XYZA

Daher können wir jetzt für \(\displaystyle \frac{dy}{dx}\) lösen und erhalten:

#XYZA

Weitere nützliche kalkül solvers

Einer der Interessanten anwendungen der Regeln von Derivaten ist das Konzept der Implizit -Unterschiede unter Differenzierung.Es ist äUzwedst Praktisch, Die aarderungsrate entlang der Kurven Zuchreiben.

Eine Andere Art von Derivaten ist Telableitungen In dem Im -Gegensatz Zum Fall Einer Impliziten differenzierung, bei Wir Annehmen, Dass y = y (x), in Dieem Fall y als Konstante AnteseHen Wird, verenn x äsdert.