Dieser scheitelpunkt -formelrechner

Dieser Taschenrechner ermöglicht es, das anzuwenden Scheitelpunktform für eine gegebene quadratische Funktion, die Sie bereitstellen.Diese quadratische Funktion muss gültig sein, wie z. B. 2x^2 + 3x + 1/3, oder sie kann nicht festgelegt werden, wie z.Die gültige gültige quadratische Funktion erfolgt.

Sobald Sie eine gültige quadratische Funktion angegeben haben, müssen Sie auf die Schaltfläche "Berechnen" klicken, und die Schritte der Anwendung der Scheitelpunktformel werden angezeigt, wobei die Schritte zur Berechnung des Scheitelpunkts der Parabel berechnet werden.

Quadratische Funktionen sind in Anwendungen in Algebra und Kalkül wirklich wichtig, und der Scheitelpunkt einer quadratischen Funktion ist sehr interpretierbar.

What is the vertex formula?

Zunächst gehen wir davon aus, dass wir mit einer quadratischen Funktion beginnen, und wir haben es vereinfacht zu:

\[ f(x) = ax^2 + bx + c \]

Dann lautet die Scheitelpunktformel für die X-Koordinate des Scheitelpunkts:

\[ x_V = \displaystyle -\frac{b}{2a}\]

Wie wende ich die scheitelpunktformel an?

• Schritt 1: Identifizieren Sie die quadratische Funktion in seiner vereinfachten Form.Sie müssen so etwas wie f (x) = ax² + bx + c haben
• Schritt 2: Aus der quadratischen Formel müssen Sie klar identifizieren, was A und B sind
• Schritt 3: Stecken Sie sie aus A und B, die Sie identifiziert haben, in die Formel XV = -B/2a

Beachten Sie, dass die Formel, wenn a = 0 ist, undefiniert ist, aber in diesem Fall wird A nicht Null sein, da wir eine quadratische Funktion haben und der Begriff, dass es sich um Multiplizierung von X² handelt, nicht Null sein kann, um eine gültige quadratische Funktion zu sein.

Warum ist es wichtig, den scheitelpunkt zu finden?

Der Scheitelpunkt verfügt).

Wenn wir also den Scheitelpunkt finden, erhalten wir bereits den extremen Punkt der quadratischen Funktion.

Beispiel: berechnen sie den scheitelpunkt

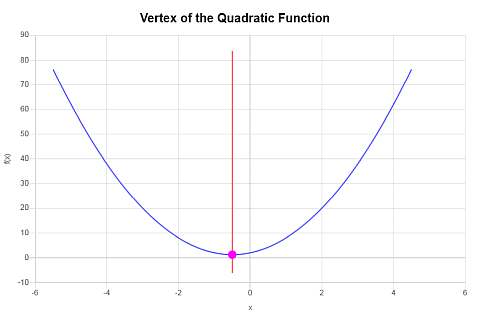
Berechnen Sie den Scheitelpunkt für die folgende quadratische Funktion: \(f(x) = 3x^2+3x+2\)

Lösung: Wir müssen die Koordinaten des Scheitelpunkts der quadratischen Funktion \(f(x) = \displaystyle 3x^2+3x+2\) finden.

Für eine quadratische Funktion des Formulars \(f(x) = a x^2 + bx + c\) wird die X-Koordinate des Scheitelpunkts unter Verwendung der folgenden Formel berechnet:

\[x_V = \displaystyle -\frac{b}{2a}\]

In diesem Fall haben wir die Funktion, für die wir den Scheitelpunkt finden müssen, für \(f(x) = \displaystyle 3x^2+3x+2\), was impliziert, dass entsprechende Koeffizienten sind:

\[a = 3\] \[b = 3\] \[c = 2\]

Stecken Sie die bekannten Werte von << xyz >> und << xyz >> in die Formel für die X-Koordinate des Scheitelpunkts, wir erhalten:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot 3} = -\frac{1}{2}\]

Jetzt müssen wir den Wert von \(x_V = \displaystyle -\frac{1}{2}\) in die quadratische Funktion anschließen, damit wir:

\[y_V = f(x_V)\] \[ = 3\cdot \left(-\frac{1}{2}\right)^2+3\cdot \left(-\frac{1}{2}\right)+2=3\cdot\frac{1}{4}+3\cdot \left(-\frac{1}{2}\right)+2=\frac{3}{4}-\frac{3}{2}+2=\frac{5}{4}\]

Daher ist der X-Koordinat des Scheitelpunkts \(x_V = \displaystyle -\frac{1}{2}\) und der y-Koordinat des Scheitelpunkts ist \(y_V = \displaystyle \frac{5}{4}\).Dies ist der Punkt, der den Scheitelpunkt darstellt, \( \displaystyle \left(-\frac{1}{2}, \frac{5}{4}\right)\).

Das Folgende wird grafisch erhalten:

Beispiel: vertex -formelanwendung

Verwenden Sie die Vertex -Formel, um die Koordinaten des mit der Funktion zugeordneten Scheitelpunkts zu berechnen \(f(x) = x^2 + 4x - \frac{3}{4}\)

Lösung: Auch hier verwenden wir die folgende Formel:

\[x_V = \displaystyle -\frac{b}{2a}\]

Da \(f(x) = \displaystyle x^2+4x-\frac{3}{4}\), was impliziert, dass entsprechende Koeffizienten sind:

\[a = 1\] \[b = 4\] \[c = -\frac{3}{4}\]

Stecken Sie die bekannten Werte von << xyz >> und << xyz >> in die Formel für die X-Koordinate des Scheitelpunkts, wir erhalten:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{4}{2 \cdot 1} = -2\]

Jetzt müssen wir den Wert von \(x_V = \displaystyle -2\) in die quadratische Funktion anschließen, damit wir:

\[y_V = f(x_V)\] \[ = 1\cdot \left(-2\right)^2+4\cdot \left(-2\right)-\frac{3}{4}=1\cdot \left(-2\right)^2+4\cdot \left(-2\right)-\frac{3}{4}=-2^2+4\cdot \left(-2\right)-\frac{3}{4}=4-8-\frac{3}{4}=-4-\frac{3}{4}=-\frac{19}{4}\]

Daher ist der X-Koordinat des Scheitelpunkts \(x_V = \displaystyle -2\) und der y-Koordinat des Scheitelpunkts ist \(y_V = \displaystyle -\frac{19}{4}\).Dies ist der Punkt, der den Scheitelpunkt darstellt, \( \displaystyle \left(-2, -\frac{19}{4}\right)\).

Dies schließt die Berechnung ab.

Beispiel: scheitelpunktanwendung

Finden Sie den extremen Punkt der Funktion \(f(x) = -2x^2 - 3x + 5\).Ist dieser extreme Punkt ein minimaler oder maximaler Punkt?

Lösung: Wir müssen die Koordinaten des Scheitelpunkts der quadratischen Funktion \(f(x) = \displaystyle -2x^2-3x+5\) finden.

Wir verwenden die folgende Formel:

\[x_V = \displaystyle -\frac{b}{2a}\]

In diesem Fall haben wir, dass die Funktion, für die wir den Scheitelpunkt finden müssen, \(f(x) = \displaystyle -2x^2-3x+5\) ist, also:

\[a = -2\] \[b = -3\]

Das bedeutet, dass:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{-3}{2 \cdot -2} = -\frac{3}{4}\]

Jetzt müssen wir den Wert von \(x_V = \displaystyle -\frac{3}{4}\) in die quadratische Funktion anschließen, damit wir:

\[y_V = f(x_V)\] \[ = \left(-2\right)\cdot \left(-\frac{3}{4}\right)^2+-3\cdot \left(-\frac{3}{4}\right)+5=\left(-2\right)\cdot\frac{9}{16}+-3\cdot \left(-\frac{3}{4}\right)+5=-\frac{9}{8}+\frac{9}{4}+5=\frac{49}{8}\]

Daher ist der X-Koordinat des Scheitelpunkts \(x_V = \displaystyle -\frac{3}{4}\) und der y-Koordinat des Scheitelpunkts ist \(y_V = \displaystyle \frac{49}{8}\).Dies ist der Punkt, der den Scheitelpunkt darstellt, \( \displaystyle \left(-\frac{3}{4}, \frac{49}{8}\right)\).

Beachten Sie, dass \(a = -2 < 0\), also öffnet sich die Parabel nach unten und der Punkt \( \displaystyle \left(-\frac{3}{4}, \frac{49}{8}\right)\) entspricht einem maximalen Punkt.Dies ist die quadratische Funktion \(f(x) = \displaystyle -2x^2-3x+5\) erreicht ein Maximum von \( \displaystyle \frac{49}{8}\) at \( x = -\frac{3}{4}\)

Mehr quadratische taschenrechner

Viele können mit quadratischen Funktionen erfolgen.Sie können die berechnen Wurzeln Einer Quadratischen Gleisung , du kannst Funde sie Die Symmetriseachse einer quadratischen Funktion und so weiter und so weiter.

Anwenden des Scheitelpunktform ist eng mit der Anwendung des Quadratische Formel und die Symmetriseachse .