Funciones racionales

Esta calculadora de funciones racionales te permitirá analizar los puntos más relevantes de una función racional que proporciones, con todos los pasos mostrados. Normalmente, para la mayoría de las funciones racionales puedes encontrar intersecciones, asíntotas verticales y su gráfica. Algunas funciones racionales específicas también tendrán asíntotas horizontales.

El tipo de función que puede proporcionar es como 'f(x)=1/x - x', o algo que involucre polinomios de mayor grado como 'f(x) = (x^3-1)/(x^2+x )'

Una vez que se haya proporcionado una función racional válida, puede hacer clic en el botón calcular y obtendrá todos los pasos que se le muestran.

Uno de los principales atributos de una función racional es que principalmente se puede reducir el cálculo al problema de resolver ecuaciones polinómicas , que es uno de los tipos "más simples" de ecuaciones que puedes resolver .

¿qué es una función racional?

Una función racional es una función que involucra la cociente de dos polinomios \(P(x)\) y \(Q(x)\), donde el divisor \(Q(x)\) no es igual al polinomio cero. Entonces, la fórmula de la función racional es

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \]

Por ejemplo, la función

\[\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \]

es una función racional, porque es precisamente el cociente de dos polinomios. pero por ejemplo

\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{\sin x} \]

no es racional porque el divisor no es un polinomio. Observa que cuando decimos que el divisor \(Q(x)\) no es igual al polinomio cero, NO estamos diciendo que \(Q(x)\) no puede tener ceros. Por ejemplo, en este caso de \(\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \), el divisor es \(Q(x) = x + 1\), que tiene un uno cero, en \(x = -1\).

Lo que no queremos es algo como

\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{0} \]

porque aunque en este caso \(Q(x) = 0\) es técnicamente un polinomio, es el polinomio cero (que es cero en todas partes).

Pasos para calcular una función racional

• Paso 1: Primero, asegúrese de tener una función racional, para la cual pueda identificar el numerador P(x) y el denominador Q(x)
• Paso 2: Si no encuentra estrictamente la estructura descrita anteriormente, se detiene. Es posible que necesite agrupar términos mediante reducciones algebraicas .
• Paso 3: Necesitas encontrar los ceros reales de P(x) y Q(x), si los hay. Las conclusiones encontradas estarán estrechamente relacionadas con los ceros de P(x) y Q(x)
• Etapa 4: Para encontrar la intersección con el eje y, evalúas la función en cero calculando f(0). La intersección con el eje y estará bien definida si x = 0 no es un cero de Q(x)
• Paso 5: Para encontrar las intersecciones con el eje x, obtienes los ceros de P(x) que no son ceros de Q(x)
• Paso 6: Para encontrar asíntotas verticales, necesitas encontrar los ceros de Q(x) que no son ceros de P(x)
• Paso 7: Para encontrar asíntotas horizontales, es necesario tener que el grado de Q(x) sea mayor o igual que el grado P(x)

Observe que, como era de esperar, el análisis de una función racional depende de Encontrar ceros de un polinomio y luego juntar todas las conclusiones. .

Observe que el dominio de una función racional es toda la recta real excepto los ceros del divisor Q(x). Si hay un cero de Q(x) que también es un cero de P(x), entonces la discontinuidad puede repararse. El rango de una función racional dependerá de los grados de P(x) y Q(x).

Por qué utilizar funciones racionales

Las funciones racionales se utilizan porque son extensiones naturales de polinomios. Se pueden ver como el siguiente paso en la complejidad de una función. Como la conocemos, expresiones de polinomios Se encuentran entre las funciones más simples que podemos encontrar, pero también se encuentran entre las más útiles.

Las ecuaciones racionales suelen aparecer en problemas de mezcla más avanzados y, sin embargo, son sorprendentemente simples de manejar, siempre que los polinomios involucrados sean lo suficientemente simples. Sabemos cómo resolver ecuaciones cuadráticas , pero para polinomios de grado 3 y superiores las cosas pueden ser más complicadas.

¿las funciones polinomiales también son funciones racionales?

Sí, si P(x) es un polinomio, entonces P(x) también es racional, porque podemos escribir:

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{1} \]

y Q(x) = 1 es un polinomio real. Lo contrario no es cierto: una función racional no es necesariamente un polinomio. ¿Porqué es eso? Porque, naturalmente, a menos que Q(x) = 1, siempre que tenga \(\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \), no tendrá que todos los términos sean términos libres como lo exige la definición de un polinomio.

Más formalmente, usando Teorema Del Resto , tenemos

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} = d(x) + \frac{r(x)}{Q(x)}\]

donde \(d(x)\) es un polinomio, pero \frac{r(x)}{Q(x)} no lo es, porque el grado de r(x) es menor que el grado de Q(x).

Ejemplo: trabajar con funciones racionales

Encuentra las intersecciones y asíntotas y la gráfica de: \(f(x) = \frac{x^2-1}{x+1}\)

Solución:

Se nos ha proporcionado la siguiente función:

\[f\left(x\right)=\frac{x^2-1}{x+1}\]

Necesitamos encontrar las intersecciones y las asíntotas, si las hay. Después de eso, se presentará la gráfica de la función.

Encontremos los ceros de la función dada. Necesitamos resolver la siguiente ecuación racional:

\[\frac{x^2-1}{x+1}=0\]

Observe que para \(x \ne -1\) podemos simplificar como:

\[\frac{x^2-1}{x+1} = 0 \Rightarrow \frac{(x-1)(x+1)}{x+1} = 0 \Rightarrow x-1 = 0\]

Ecuación del numerador auxiliar

Ahora igualamos el numerador a cero y encontramos las soluciones. Entonces, aquellas raíces que no hagan que el denominador sea igual a cero serán soluciones de la ecuación racional.

Para encontrar las raíces del numerador es necesario resolver lo siguiente: \(x^2-1=0\)

Para una ecuación cuadrática de la forma \(a x^2 + bx + c = 0\), las raíces se calculan usando la siguiente fórmula:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

En este caso, tenemos que la ecuación que necesitamos resolver es \(\displaystyle x^2-1 = 0\), lo que implica que los coeficientes correspondientes son:

\[a = 1\] \[b = 0\] \[c = -1\]

Primero, calcularemos el discriminante para evaluar la naturaleza de las raíces. La discriminación se calcula como:

\[\Delta = b^2 - 4ac = \displaystyle \left( 0\right)^2 - 4 \cdot \left(1\right)\cdot \left(-1\right) = 4\]

Como en este caso obtenemos que el discriminante es \(\Delta = \displaystyle 4 > 0\), que es positivo, sabemos que la ecuación tiene dos raíces reales diferentes.

Ahora, reemplazando estos valores en la fórmula de las raíces obtenemos:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{0 \pm \sqrt{\left(0\right)^2-4\left(1\right)\left(-1\right)}}{2\cdot 1} = \displaystyle \frac{0 \pm \sqrt{4}}{2}\]

entonces, encontramos que:

\[ {x}_1 = \frac{0}{2}-\frac{1}{2}\sqrt{4}=\frac{0}{2}-1=-1 \] \[{x}_2 = \frac{0}{2}+\frac{1}{2}\sqrt{4}=\frac{0}{2}+1=1\]

Ecuación del denominador auxiliar

Necesitamos encontrar las raíces del denominador: \(x+1=0\)

Por lo tanto, resolver \(x\) para una ecuación lineal dada conduce a \(x=-1\).

Ceros del numerador y denominador

Según el análisis mostrado arriba, los ceros reales del numerador de la función racional dada son \( x_{ 1} = -1\) y \( x_{ 2} = 1\).

También se encuentra que el denominador tiene un cero real, que es \( x_{ 1} = -1\).

Encontrar intersecciones x

Con base en los ceros del numerador que no son ceros del denominador, encontramos que hay una intersección con el eje x, que es \(\left(1, 0\right)\).

Encontrar intersecciones en y

Al evaluar la función proporcionada en \(x = 0\), encontramos que:

\[ f(0) = \frac{0^2-1}{0+1} = -1\]

entonces la intersección con el eje y es \( \left(0, -1\right)\).

Asíntotas verticales

Luego de analizar los ceros, se concluye que la función no tiene asíntotas verticales.

Asíntotas horizontales

Observe que el grado del numerador es \(2\) y el grado del denominador es \(1\), y luego, como el grado del polinomio en el numerador excede al del denominador, concluimos que no hay horizontal asíntota.

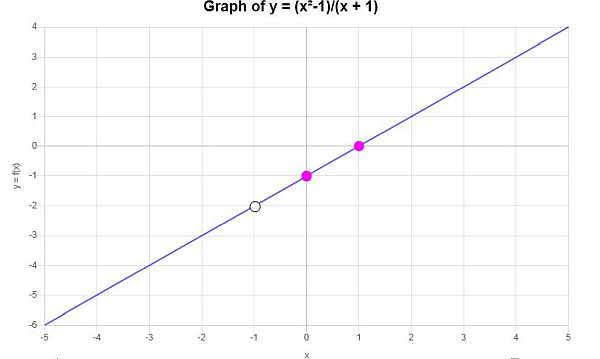
Se obtiene la siguiente gráfica:

Ejemplo: asíntotas horizontales

¿Esta función racional tiene asíntota horizontal: \(f(x) = \frac{x^2-1}{x^2+1}\)?

Solución: Claramente en este caso la función consta del cociente de dos polinomios, y ambos tienen grado igual a 2. Es decir, tienen el mismo grado y por tanto, hay una asíntota horizontal.

También podemos ver esto usando límites:

\[\lim_{x\to +\infty} f(x) = \lim_{x\to +\infty}\frac{x^2-1}{x^2+1} = \lim_{x\to +\infty}\frac{1-\frac{1}{x^2}}{1+\frac{1}{x^2}} = 1\]

lo que implica que la asíntota horizontal es \(y = 1\). Con esto concluye el cálculo.

Calculadoras de funciones útiles

Las funciones son objetos matemáticos fundamentales, que resumen la relación entre diferentes variables. Usando un Calculadora de funciones puede ayudarle a abordar sistemáticamente funciones que pueden ser demasiado complicadas para manejarlas manualmente.

Graficar funciones racionales es uno de los ejemplos de juguetes más comunes que los estudiantes aprenden en Álgebra y Cálculo, y aunque quizás las funciones racionales no aparecen per se con tanta frecuencia en las aplicaciones, las habilidades analíticas necesarias para lidiar con ellas pueden resultar invaluables

Lo mismo va para Resolver ecuaciones racionales , donde los principios de manipular expresiones algebraicas y reducirlas a sus términos inferiores serán extremadamente poderosos para el logro de habilidades más avanzadas.

Ahora bien, si hablamos de función, no podemos olvidarnos de la cálculo de la derivada de una función , integración y otras técnicas infinitesimales más avanzadas.