Calculadora de derivadas

Esta calculadora de derivadas te guiará a través de todos los pasos y reglas que se usan para encontrar la derivada de una función determinada. Tienes que escribir una función como 3x + sin(x^2), o puedes anteponerla con la definición completa de la función, como f(x) = 3x^ 2 + 2tan(x^3).

Tenga en cuenta que esto se puede denominar una calculadora de primera derivada al igual que una calculadora de derivada. La primera derivada y la derivada representan lo mismo, y la "primera" parte generalmente se elimina.

La función provista puede venir completamente simplificada o no, no importa, ya que la calculadora primero simplificará la función si es necesario antes de calcular su derivada.

Una vez función válida se ha proporcionado, solo necesita hacer clic en "Calcular", esperar unos segundos y se le presentarán todos los pasos del cálculo.

La diferenciación es la herramienta principal utilizada en cálculo (junto con la integración) y es una operación crucial que se usa ampliamente en matemáticas más avanzadas. Algunas aplicaciones muy comunes incluyen cálculo de la línea tangente , máximos y mínimos y mucho más.

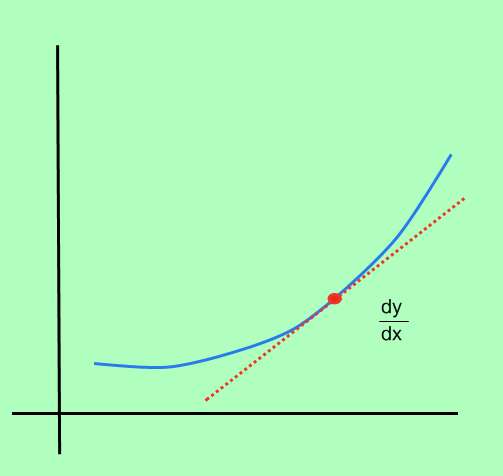
¿cómo calcular la derivada de una función?

El proceso de calcular la derivada de una función se llama diferenciación , y consiste en determinar la tasa de cambio instantánea del punto, en cada punto del dominio de la función.

¿Cuál es la tasa de cambio instantánea de una función? Bueno, comencemos con la definición de tasa de cambio : Considere una función \(f\) y suponga que tenemos dos puntos, \(x_0\) y \(x_1\). En el punto \(x_0\), la función es \(f(x_0)\), y en el punto \(x_1\), la función toma el valor \(f(x_1)\)

Entonces, el cambio en f se define como \(\Delta y = f(x_1) - f(x_0)\) (que también se conoce como el cambio en y). Además, el cambio en x se define como \(\Delta x = x_1 - x_0)\). En palabras simples, \(\Delta x\) es el cambio en x, mientras que \(\Delta y\) es el cambio en el valor de la función, debido al cambio en x.

Gráficamente:

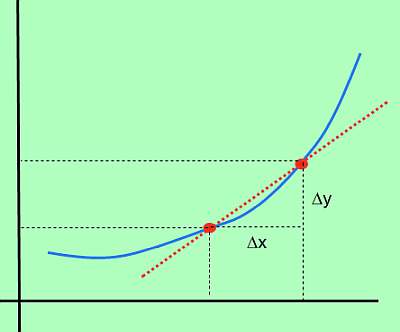
Fórmula derivada

Entonces, si \(\Delta x\) representa el cambio en x, y \(\Delta y\) representa el cambio en el valor de la función, debido al cambio en x, el correspondiente tasa de cambio es:

\[\text{Rate of Change} = \displaystyle \frac{\Delta y}{\Delta x} \]

Entonces, ¿cuál sería la tasa de cambio instantánea? Eso correspondería a analizar qué pasaría si \(\Delta x\) se vuelve realmente pequeño. Uno esperaría que \(\Delta y\) también se hiciera pequeño, pero ¿eso sucedería con la tasa entre \(\Delta y\) y \(\Delta x\)?

Entonces, en este contexto, la tasa de cambio instantánea se define como

\[\text{Instant Rate of Change} = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} \]

Entonces, en términos simples, establecemos \(x_0\) fijo y calculamos la tasa de cambio para los valores de \(x_1\) que están más y más cerca de \(x_0\). Usando esta idea de tasa de cambio instantánea, podemos dar la siguiente fórmula para la derivada en un punto \(x_0\).

\[f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \]

Si el límite anterior existe, decimos que la función f es diferenciable en \(x_0\). Además, diremos que una función es diferenciable en un conjunto A, si la función es diferenciable en todos los puntos del conjunto.

Pasos para usar la fórmula de la derivada

• Paso 1: Identifique claramente la función f que desea diferenciar
• Paso 2: Asegúrese de simplificar f tanto como sea posible, de lo contrario, encontrar el límite requerido puede ser innecesariamente más difícil
• Paso 3: Decide si trabajarás con un punto genérico x0 o si estás dando un punto numérico específico para x0
• Etapa 4: Según la definición de la función, utilice la fórmula \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \). Esto es, sustituya los valores de x0 y x1 en f, y vea cómo se ve la fórmula algebraicamente
• Paso 5: Simplifique todo lo que pueda ANTES de tomar el límite
• Paso 6: A veces es más fácil establecer x1 = x0 + h, y luego calcular el límite cuando h converge a 0

Tenga en cuenta que el Paso 6 es uno que a algunas personas les gusta como predeterminado. De hecho, la fórmula de la derivada alternativa que puede parecer más sencilla a efectos de simplificación es:

\[f'(x_0) = \displaystyle \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h} \]

que es la fórmula que puede encontrar en su libro de texto, en lugar del otro.

Reglas derivadas

Parecería mucho trabajo calcular la derivada usando la fórmula. Y, de hecho, podría ser un proceso laborioso si decidiéramos resolver todos los procesos de diferenciación usando la fórmula de la derivada.

Afortunadamente, hay una serie de funciones (a saber, polinomios , funciones trigonométricas ) por lo que sabemos con precisión cuáles son sus derivadas.

Además de eso, tenemos reglas de diferenciación que nos permiten encontrar la derivada de una función que es un Función compuesta y/o una combinación de funciones elementales (de las que conocemos su derivada), en términos de derivadas elementales.

¿cuáles son los pasos para calcular la derivada?

• Paso 1: Identifique la función que desea diferenciar. Simplifica todo lo que puedas ANTES de calcular su derivada
• Paso 2: Determine si está obligado o no a utilizar la fórmula derivada o no
• Paso 3: Si debe usar la fórmula derivada, use \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \), o puede usar \(f'(x_0) = \displaystyle \lim_{h \to 0}\frac{f(x_0+h) - f(x_0)}{h} \) si parece más fácil de abordar
• Etapa 4: Si no está obligado a utilizar la fórmula derivada, puede utilizar las principales reglas de diferenciación: Linealidad, Regla Del Producto , Regla Del Cociente y Cadena De Reglas , que te ayudará a reducir el cálculo de la derivada al uso de derivadas básicas conocidas

A menudo, la función que intenta encuentra la derivada for no es una función simple, sino que es una combinación básica de varias funciones simples. Por ejemplo, la función

\[f(x) = x + \cos(x) + \sin(x)\]

no es una función elemental en sí misma, pero es Función compuesta de tres funciones elementales, \(x\), \(\sin x\) y \(\cos x\).

Aplicaciones de los derivados

Uno podría pensar "bueno, las derivadas involucran límites y eso es súper teórico, entonces no debe tener demasiadas aplicaciones", pero estaría completamente equivocado. La magia de las derivadas es que tratan esencialmente de la tasa de cambio de funciones, que pueden representar diferentes tipos de procesos.

Es por ello que la diferenciación permite estudiar el proceso de cambio, y cómo comparar variables cambiantes, lo cual tiene una amplia aplicabilidad.

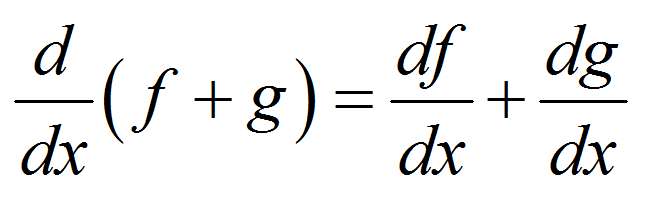
Ejemplo: cálculo de la derivada

Calcular la derivada con respecto a x para \(f(x) = \displaystyle \frac{x}{3} + \frac{5}{4} \cos(x) - \frac{5}{4} \sin(x^2)\)

Solución: Se ha proporcionado la siguiente función: \(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\), para la cual necesitamos calcular su derivada.

Paso Inicial: En este caso, primero necesitamos simplificar la función dada \(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right) \), y para hacerlo, llevamos a cabo los siguientes pasos de simplificación:

Después de simplificar la función, podemos proceder al cálculo de la derivada:

Se obtiene el siguiente gráfico para \(\displaystyle f(x)=\frac{1}{3}x+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\) en el intervalo \([-5, 5]\):

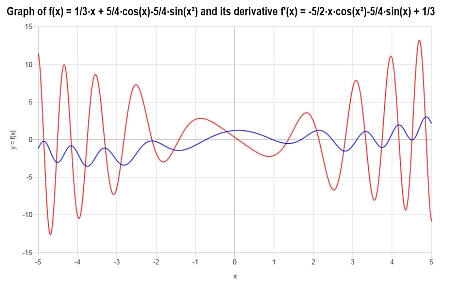
Ejemplo: derivar una función

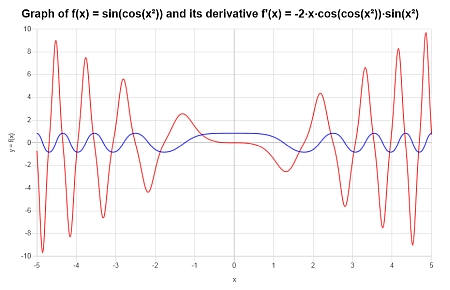
Calcule la derivada de: \(f(x) = \sin(\cos(x^2))\) y proporcione la gráfica de \(f(x)\) y \(f'(x)\).

Solución: Ahora tenemos \(\displaystyle f(x)=\sin\left(\cos\left(x^2\right)\right)\).

La función ya viene simplificada, por lo que podemos proceder directamente a calcular su derivada. Usando esta derivación cal obtenemos:

Por lo tanto, obtenemos el siguiente gráfico para la función en el intervalo \([-5, 5]\):

Ejemplo: calculadora de derivadas

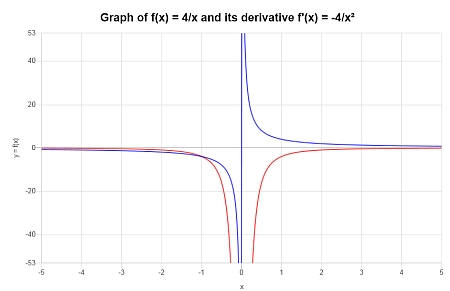
Encuentra la derivada de \( f(x) = \displaystyle \frac{4}{x}\). ¿Está bien definido en todas partes? Gráficalo.

Solución: La función provista para la cual se necesita la derivada es \(\displaystyle f(x)=\frac{4}{x}\).

No se necesita más simplificación, por lo que podemos proceder directamente a calcular su derivada:

Gráficamente:

Más sobre derivadas y funciones

Este calculadora de derivadas con pasos te resultará muy útil ya que realizará el cálculo de la derivada de cualquier función dada, mostrando todos los pasos del proceso, aplicando los Reglas Derivadas , e indicándole cuándo se están aplicando y por qué.

Esta calculadora también se puede llamar calculadora dy dx o calculadora de cociente diferencial como eso es precisamente lo que hace, calcula el límite de la relación dy/dx cuando dx se aproxima a 0.

Las funciones son construcciones extremadamente importantes en matemáticas. Junto con la diferenciación, debe ser capaz de simplificar una función por lo general, como preámbulo de otros cálculos más especializados. Existen tipos especiales de funciones que le permiten realizar operaciones específicas, como lo que hace con Operaciones con polinomios .

Curiosamente, muchos elementos importantes como encontrar las coordenadas de la vértice de una parábola que se puede derivar de manera inteligente usando argumentos geométricos, se puede obtener de forma trivial usando diferenciación.

Asimismo, la idea de Linea tangente y Aproximación De Primer Orden aparecen de forma natural, a partir del concepto de derivada, y una extensión natural.