Una calculadora de funciones

Esta calculadora le permitirá calcular, simplificar y graficar cualquier función válida que proporcione, mostrando todos los pasos de simplificación. Debe proporcionar una función válida a la calculadora. Puede ser algo ya simplificado como f(x) = 2x + 3, podría ser algo más complejo que requiera simplificación, como f(x) = (1/3+1/4)x + x^2 - sin( 1/5+1/6) + 3/4'.

Cuando se proporciona una función válida, simplemente puede hacer clic en el botón "Calcular" y el proceso de simplificación y graficacion de la funcion se le mostrará a usted.

Las funciones son los objetos más importantes en Álgebra y Cálculo, y ser capaz de calcular y simplificar expresiones puede hacer toda la diferencia.

¿cómo calcular la función?

La idea de calcular una función se basa simplemente en la definición de una función, donde para un valor dado, a \(x\) se le asigna una 'imagen' que se llama \(f(x)\).

En el siguiente gráfico, puede ver cómo a un valor "x" en el eje x se le asigna un punto "f(x)" en el eje y:

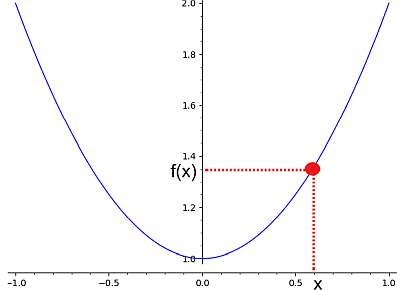
Entonces, la idea del cálculo de una función es obtener un valor "x" y poder calcular el valor de "f(x)". Ahora, a veces eso es posible para algunos valores de x, a veces para todos los valores de x en la línea real. El conjunto de valores x donde se puede calcular f(x) se llama dominio de una función

¿cuáles son los pasos para calcular una función?

• Paso 1: Identificar la expresión que determina la función
• Paso 2: simplifica la función tanto como puedas, pero ten en cuenta las posibles divisiones por cero
• Paso 3: Tome nota de dónde se puede y no se puede calcular la función

Así que a medida que avanzas con esto proceso de simplificación , habrá anotado los valores en los que la función no se puede evaluar (si corresponde). De esta manera, indirectamente has encontrado el dominio de la función.

Por ejemplo, si tiene una función como f(x) = 2x + 1, independientemente del punto que elija para x, la expresión '2x + 1' siempre se puede evaluar. Pero en cambio, si tiene la función f(x) = 1/x, si elige x = 0, no podrá calcular la función en x = 0, porque eso se convertiría en 1/0, y una división por cero es indefinido.

¿cómo simplificar funciones?

El proceso de simplificación de funciones es como cualquier simplificación de expresiones : se utilizan los criterios definidos por el regla PEMDAS para llevar a cabo cualquier posible simplificación.

Pero hay un par de advertencias al usar PEMDAS: debe evitar divisiones inadvertidas por cero o sacar raíces cuadradas de números negativos. Por ejemplo, considere la función

\[ f(x) = \displaystyle\frac{2x}{x}\]

Podrías pensar, bueno, cancelaré x, y luego obtendré:

\[\displaystyle f(x) = \displaystyle \frac{2\cancel{x}}{\cancel{x}} = 2\]

Pero al hacerlo estarías cometiendo un error, porque tal cancelación de x no puede ocurrir cuando x = 0. Lo que podrías hacer es escribir explícitamente

\[\displaystyle f(x) = \displaystyle \frac{2\cancel{x}}{\cancel{x}} = 2\]

para \(x \ne 0\), e indefinido para \(x = 0\).

¿cuáles son los pasos para simplificar?

• Paso 1: identifique la función proporcionada y asegúrese de que sea una expresión simbólicamente válida
• Paso 2: Simplifica los términos tanto como sea posible usando la regla PEMDAS, teniendo cuidado de no obtener divisiones por cero o raíces cuadradas negativas.
• Paso 3: Toma nota de aquellos puntos donde la función no puede ser evaluada. El dominio de la función será el complemento de esos puntos en la recta real

muchas veces, es bastante fácil detectar puntos donde podría haber un problema al evaluar la función, mediante una simple inspección de la estructura de la función.

¿puedes calcular una función a partir de puntos?

Eso depende. El proceso de encontrar una función a partir de puntos dados se llama interpolación . Ahora, para un conjunto dado de puntos, habrá más de una función que pase por esos puntos, por lo que, en cierto modo, dar puntos por sí solo no necesariamente determinará UNA función.

Ahora, agregar ciertas restricciones podría hacer que la determinación sea única. Por ejemplo, para dos puntos dados, sólo hay uno función lineal (afín lineal, para ser más precisos) que los atraviesa. O dados tres puntos, solo hay uno función cuadrática que pasa a través de ellos.

Ejemplo: cálculo de función

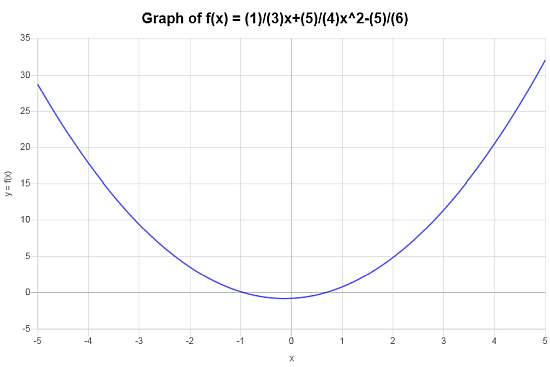
Calcular y graficar la función: \(f(x) = \frac{1}{3}x + \frac{5}{4}x^2 - \frac{5}{6}\)

Solución: Se ha proporcionado la siguiente función: \(\displaystyle f(x)=\frac{1}{3}x+\frac{5}{4}x^2-\frac{5}{6}\), para lo cual necesitamos simplificar y construir su gráfica.

Paso 0: En este caso, primero necesitamos simplificar la función dada \(\displaystyle f(x)=\frac{1}{3}x+\frac{5}{4}x^2-\frac{5}{6} \), y para hacerlo, notamos que:

Se obtiene el siguiente gráfico para \(\displaystyle f(x)=\frac{5}{4}x^2+\frac{1}{3}x-\frac{5}{6}\) en el intervalo \([-5, 5]\):

Ejemplo: ejemplo de calculadora de funciones

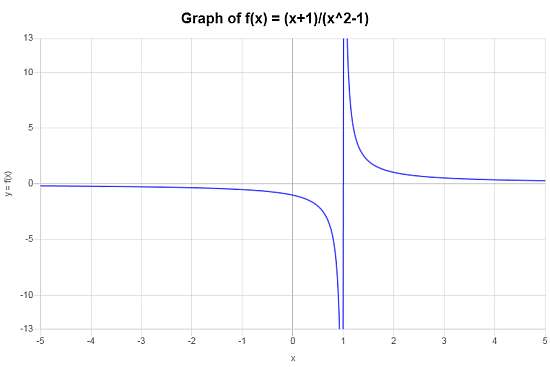
Calcula el dominio de la siguiente función: \(f(x) = \displaystyle \frac{x+1}{x^2-1}\)

Solución: La función provista \(\displaystyle f(x)=\frac{x+1}{x^2-1}\) se puede simplificar de la siguiente manera:

\[ f(x) = \displaystyle \frac{x+1}{x^2-1} = \displaystyle \frac{x+1}{(x-1)(x+1)} = \displaystyle \frac{1}{x-1} \]

pues cuando \(x \ne 1\). Por lo tanto, el dominio de la función es \((-\infty, 1) \cup (1,\infty)\). Se obtiene el siguiente gráfico para la función en el intervalo \([-5, 5]\):

Ejemplo: otro ejemplo de calculadora de funciones

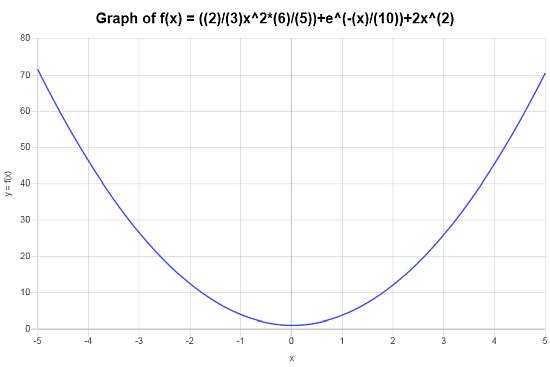
Simplifica y representa gráficamente \( f(x) = \left(\frac{2}{3}x^2 \times \frac{6}{5} \right)+ e^{-x/10} + 2x^2 \).

Solución: Contamos con: \(\displaystyle f(x)=\frac{2}{3}x^2\cdot \frac{6}{5}+e^{\left(-1\right)x/10}+2x^2\). Ahora, para simplificar la función dada \(\displaystyle f(x)=\frac{2}{3}x^2\cdot \frac{6}{5}+e^{\left(-1\right)x/10}+2x^2 \), hacemos:

Por lo tanto, se obtiene el siguiente gráfico para \(\displaystyle f(x)=\frac{14}{5}x^2+e^{\left(-1/10\right)x}\) en el intervalo \([-5, 5]\):

Otras calculadoras de funciones

La idea de función es central en Álgebra y Cálculo. Hay muchas cosas que puedes hacer con las funciones. Una de las principales habilidades que puedes desarrollar es sentirte cómodo simplificar expresiones , para reducir la función dada a una más simple.

Solo asegúrese de no tener un gatillo feliz y terminar cancelando ceros y sacando raíces cuadradas de números negativos.

Además, es posible que desee simplemente graficar una función , para tener una mejor idea de cómo se ve la función y cuáles son sus principales propiedades.