Calculadora de ecuaciones racionales
Instrucciones: Utilice esta calculadora de ecuaciones racionales para calcular la solución de cualquier ecuación racional que proporcione, mostrando todos los pasos. Por favor escriba la ecuación que desea resolver en el cuadro a continuación.
Resolver ecuaciones racionales
Con esta calculadora con pasos podrás trabajar fácilmente resolviendo ecuaciones racionales. La forma en que esto funciona es que simplemente debes proporcionar una ecuación racional en el cuadro de arriba. Esta ecuación podría ser tan simple como 'x^(1/2) = x^(1/4)', o más complicada si es necesario.
Luego, cuando haya terminado de escribir o pegar la ecuación que desea, puede hacer clic en el botón "Resolver", que resuelve la ecuación y le mostrará todos los pasos del camino.
Las ecuaciones racionales, como otros tipos de ecuaciones no lineales, serán en general difíciles de resolver, si es que puedes resolverlas. Por lo general, sólo ciertos Ecuaciones racionales , con ciertas estructuras específicas se podrá resolver explícitamente usando algunos trucos estándar, como el uso de sustituciones.

¿qué es una ecuación racional?
Una ecuación racional es un tipo de ecuación que se encuentra en álgebra en la que en algún punto de la ecuación se ve un cociente de dos polinomios. Por ejemplo
\[\displaystyle \frac{x}{x+1} + 4 = 1\]es una ecuación racional, debido al término \(\frac{x}{x+1} \). Técnicamente, todas las ecuaciones polinómicas también son ecuaciones racionales, porque un polinomio siempre puede considerarse dividido por 1, y 1 es un polinomio de orden 0 (una constante).
Lo anterior es una forma elegante de expresar este \(P(x) = \frac{P(x)}{1}\).
Fórmula de ecuación racional
No existe una fórmula específica para una ecuación racional, pero deberías poder identificarlas siempre que aparezca el cociente de dos denominadores en una ecuación. En términos de fórmula, estás intentando identificar algo como:
\[\displaystyle \frac{P(x)}{Q(x)} \]en algún lugar de la ecuación, para clasificarla como una ecuación racional.
Cómo resolver ecuaciones racionales
- Paso 1: Primero asegúrate de que realmente estás tratando con una ecuación racional. Es muy probable que un tipo diferente de ecuación requiera un enfoque diferente
- Paso 2: Examina la estructura e intenta ver si una sustitución convierte la ecuación rápidamente en una ecuación polinómica
- Paso 3: Si no es posible realizar una sustitución rápida, debe ir por el camino más largo: encontrar denominadores comunes en ambos lados de la ecuación y multiplicar esos denominadores. Esto conducirá directamente a una ecuación polinómica
Por ejemplo, si necesitas resolver esta ecuación racional \(\frac{1}{x} + \frac{1}{x^2} = 2\), podrías seguir el método más largo para encontrar el denominador común, que en este caso sería \(x^2\) y terminarías en una ecuación polinómica.
Pero entonces, también puedes hacer la sustitución \(u = \frac{1}{x}\), entonces la ecuación se convierte en la ecuación auxiliar \(u + u^2 = 2\), que se puede resolver inmediatamente usando el Fórmula de ecuación cuadrática .
Relación con las expresiones racionales
expresiones racionales y simplificación de la expresión racional Es una tarea crucial a la hora de resolver ecuaciones que involucran expresiones racionales.
Pero al mismo tiempo, antes de precipitarse ciegamente a simplificar y operar la ecuación en cuestión, querrá evaluar si existe o no una sustitución que reducirá las cosas a una ecuación auxiliar muy simple.

Cómo utilizar esta calculadora de ecuaciones racionales con pasos
La ventaja de nuestra calculadora es que hará el cálculo mostrándote los pasos, lo que sin duda te puede resultar útil. Sin embargo, lo principal es que no todas las ecuaciones racionales tendrán una solución que podamos encontrar utilizando métodos elementales.
resolver ecuaciones A veces requiere un poco de astucia, pero con nuestra calculadora eliminarás las conjeturas.

Ejemplo: una ecuación racional simple
Resuelve la siguiente ecuación: \(\frac{1}{x} + \frac{1}{x^2} = 2\)
Solución: Nos proporciona la siguiente ecuación
\[\frac{1}{x}+\frac{1}{x^2}=2\]Usamos la sustitución: \(u = \frac{1}{x}\) por lo que la ecuación queda:
\[u + u^2 = 2\]Esta ecuación cuadrática se puede expresar como \(u^2 + u - 2 = (u-1)(u+2) = 0\)
lo que conduce directamente a las soluciones \(u = 1, u = -2\). Pero como sabemos que \(u = \frac{1}{x}\), encontramos la siguiente solución a la ecuación original:
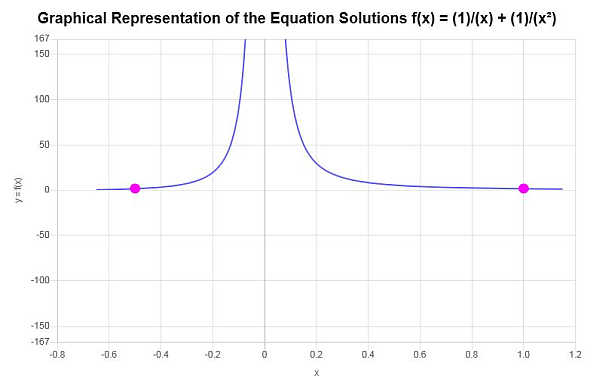
\[x_1 = -\frac{1}{2} \] \[x_2 = 1 \]Por lo tanto, resolver \(x\) para la ecuación dada conduce a las soluciones \(x=-\frac{1}{2},\,\,x=1\).
Gráficamente
La siguiente es la representación gráfica de las soluciones obtenidas:
Más calculadoras de ecuaciones
Mayoría Calculadoras de ecuaciones explotará estructuras específicas para intentar encontrar una solución exacta, pero los esfuerzos no siempre tendrán éxito.
Pero en última instancia, no hay mucho que se pueda hacer en general. Lo único que podemos hacer es Resolver Ecuaciones Lineales y resolver ecuaciones polinómicas (hasta cierto punto, sólo ecuaciones cuadráticas son realmente sencillos de resolver).
Entonces, cualquier estrategia para resolver una ecuación tiene que ver con transformarla un poco usando algunos reducción algebraica en los pocos tipos de ecuaciones que realmente sabemos cómo resolver. Y sobre todo, todo lo que podemos hacer es probar algunas sustituciones afortunadas, si tienes la suerte.



