Esta calculadora de fórmula de vértice

Esta calculadora permitirá aplicar la fórmula de vértice para una función cuadrática dada que proporcione. Esta función cuadrática debe ser válida, como 2x^2 + 3x + 1/3, o puede venir sin simplificar, como 2x^2 - x + 5 - 3/4 x^2 +1/3, etc. Cualquiera función cuadrática válida válida servirá.

Una vez que proporcione una función cuadrática válida, debe hacer clic en el botón "Calcular", y se mostrarán los pasos de la aplicación de la fórmula del vértice, con los pasos seguidos para calcular el vértice de la parábola.

Las funciones cuadráticas son realmente importantes en aplicaciones de Álgebra y Cálculo, y el vértice de una función cuadrática es muy interpretable.

¿cuál es la fórmula del vértice?

Primero, asumimos que comenzamos con una función cuadrática, y la hemos simplificado a:

\[ f(x) = ax^2 + bx + c \]

Entonces, la fórmula del vértice para la coordenada x del vértice es:

\[ x_V = \displaystyle -\frac{b}{2a}\]

¿cómo aplicar la fórmula del vértice?

• Paso 1: Identifica la función cuadrática en su forma simplificada. Necesitas tener algo como f(x) = ax²+ bx + c
• Paso 2: a partir de la fórmula cuadrática, debe identificar claramente qué son a y b
• Paso 3: De a y b que identificaste, conéctalos a la fórmula xv = -b/2a

Note que si a = 0, entonces la fórmula será indefinida, pero en este caso a no será cero, ya que tenemos una función cuadrática, y el término que multiplica x² no puede ser cero para ser una función cuadrática válida.

¿por qué es importante encontrar el vértice?

El vértice tiene una propiedad muy importante, que es el punto donde la función cuadrática alcanza su mínimo (cuando abre hacia arriba cuando a > 0) o es el punto donde la función cuadrática alcanza su máximo (cuando abre hacia abajo cuando a > 0) ).

Entonces, al hallar el vértice ya estamos obteniendo el punto extremo de la función cuadrática.

Ejemplo: calcular vértice

Calcula el vértice de la siguiente función cuadrática: \(f(x) = 3x^2+3x+2\)

Solución: Necesitamos encontrar las coordenadas del vértice de la función cuadrática \(f(x) = \displaystyle 3x^2+3x+2\).

Para una función cuadrática de la forma \(f(x) = a x^2 + bx + c\), la coordenada x del vértice se calcula usando la siguiente fórmula:

\[x_V = \displaystyle -\frac{b}{2a}\]

En este caso, tenemos que la función para la que necesitamos encontrar el vértice es \(f(x) = \displaystyle 3x^2+3x+2\), lo que implica que los coeficientes correspondientes son:

\[a = 3\] \[b = 3\] \[c = 2\]

Reemplazando los valores conocidos de \(a\) y \(b\) en la fórmula para la coordenada x del vértice, obtenemos:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot 3} = -\frac{1}{2}\]

Ahora, necesitamos reemplazar el valor de \(x_V = \displaystyle -\frac{1}{2}\) en la función cuadrática, por lo que obtenemos:

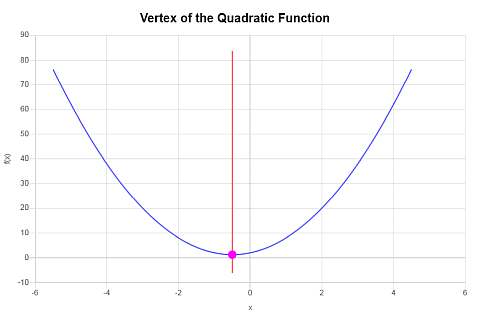
\[y_V = f(x_V)\] \[ = 3\cdot \left(-\frac{1}{2}\right)^2+3\cdot \left(-\frac{1}{2}\right)+2=3\cdot\frac{1}{4}+3\cdot \left(-\frac{1}{2}\right)+2=\frac{3}{4}-\frac{3}{2}+2=\frac{5}{4}\]

Por lo tanto, la coordenada x del vértice es \(x_V = \displaystyle -\frac{1}{2}\), y la coordenada y del vértice es \(y_V = \displaystyle \frac{5}{4}\). Este, el punto que representa el vértice es \( \displaystyle \left(-\frac{1}{2}, \frac{5}{4}\right)\).

De forma gráfica se obtiene lo siguiente:

Ejemplo: aplicación de fórmula de vértice

Usa la fórmula del vértice para calcular las coordenadas del vértice asociado a la función \(f(x) = x^2 + 4x - \frac{3}{4}\)

Solución: Nuevamente, usamos la siguiente fórmula:

\[x_V = \displaystyle -\frac{b}{2a}\]

Dado que \(f(x) = \displaystyle x^2+4x-\frac{3}{4}\), lo que implica que los coeficientes correspondientes son:

\[a = 1\] \[b = 4\] \[c = -\frac{3}{4}\]

Reemplazando los valores conocidos de \(a\) y \(b\) en la fórmula para la coordenada x del vértice, obtenemos:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{4}{2 \cdot 1} = -2\]

Ahora, necesitamos reemplazar el valor de \(x_V = \displaystyle -2\) en la función cuadrática, por lo que obtenemos:

\[y_V = f(x_V)\] \[ = 1\cdot \left(-2\right)^2+4\cdot \left(-2\right)-\frac{3}{4}=1\cdot \left(-2\right)^2+4\cdot \left(-2\right)-\frac{3}{4}=-2^2+4\cdot \left(-2\right)-\frac{3}{4}=4-8-\frac{3}{4}=-4-\frac{3}{4}=-\frac{19}{4}\]

Por lo tanto, la coordenada x del vértice es \(x_V = \displaystyle -2\), y la coordenada y del vértice es \(y_V = \displaystyle -\frac{19}{4}\). Este, el punto que representa el vértice es \( \displaystyle \left(-2, -\frac{19}{4}\right)\).

Esto concluye el cálculo.

Ejemplo: aplicación vertex

Encuentra el punto extremo de la función \(f(x) = -2x^2 - 3x + 5\). ¿Este punto extremo es un punto mínimo o máximo?

Solución: Necesitamos encontrar las coordenadas del vértice de la función cuadrática \(f(x) = \displaystyle -2x^2-3x+5\).

Usamos la siguiente fórmula:

\[x_V = \displaystyle -\frac{b}{2a}\]

En este caso, tenemos que la función para la cual necesitamos encontrar el vértice es \(f(x) = \displaystyle -2x^2-3x+5\), entonces:

\[a = -2\] \[b = -3\]

Esto significa que:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{-3}{2 \cdot -2} = -\frac{3}{4}\]

Ahora, necesitamos reemplazar el valor de \(x_V = \displaystyle -\frac{3}{4}\) en la función cuadrática, por lo que obtenemos:

\[y_V = f(x_V)\] \[ = \left(-2\right)\cdot \left(-\frac{3}{4}\right)^2+-3\cdot \left(-\frac{3}{4}\right)+5=\left(-2\right)\cdot\frac{9}{16}+-3\cdot \left(-\frac{3}{4}\right)+5=-\frac{9}{8}+\frac{9}{4}+5=\frac{49}{8}\]

Por lo tanto, la coordenada x del vértice es \(x_V = \displaystyle -\frac{3}{4}\), y la coordenada y del vértice es \(y_V = \displaystyle \frac{49}{8}\). Este, el punto que representa el vértice es \( \displaystyle \left(-\frac{3}{4}, \frac{49}{8}\right)\).

Note que \(a = -2 < 0\), entonces la parábola abre hacia abajo, y el punto \( \displaystyle \left(-\frac{3}{4}, \frac{49}{8}\right)\) corresponde a un punto máximo. Es decir, la función cuadrática \(f(x) = \displaystyle -2x^2-3x+5\) alcanza un máximo de \( \displaystyle \frac{49}{8}\) en \( x = -\frac{3}{4}\)

Más calculadoras cuadráticas

Se pueden hacer muchas cosas con funciones cuadráticas. Puedes calcular el raíces de una ecuación cuadrática , puedes encuentra el eje de simetria de una función cuadrática, y así sucesivamente.

Aplicando el fórmula de vértice está estrechamente relacionado con la aplicación de la Fórmula cuadrática y el Eje de simetria .