Más sobre desigualdades polinómicas

Esta calculadora puede ayudarle con la solución de desigualdades polinómicas, mostrándole todos los pasos del proceso de cálculo de la solución, además de proporcionarle una gráfica de desigualdad que representa la solución

La desigualdad que proporcionas puede ser algo simple como 'x^2 > 1', o podría ser algo más complejo como 'x^3 + 3x^2 + 3x + 1 > 0'.

Una vez que se proporcione una desigualdad polinómica válida, continúe y haga clic en el botón "Calcular" para obtener la solución y todos los pasos que se muestran.

Tenga en cuenta que no todos los polinomios que proporcione se prestarán a soluciones exactas. Cuanto menor sea el grado del polinomio, más probable será encontrar una solución exacta a la desigualdad.

¿qué es una desigualdad polinómica?

Una desigualdad polinómica es simplemente un tipo de desigualdad en la que las expresiones involucradas son polinomiales y ninguno de sus términos es una expresión no polinómica. Por ejemplo

\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \displaystyle \frac{x^3}{3} \]

es una desigualdad polinómica, mientras que

\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \sin(x) \]

es un no, debido a la presencia del término \(\sin x\), que no es un polinomio. Resolver desigualdades En general, es un proceso difícil, pero para los polinomiales tenemos un plan de acción claro.

¿cómo se resuelve una desigualdad polinómica?

• Paso 1: Asegúrate de que todos los términos sean polinomios. De lo contrario, es posible que los métodos específicos utilizados para polinomios no se apliquen
• Paso 2: Pon todo de un lado, dejando cero del otro lado
• Paso 3: Reemplazando el signo de desigualdad por "=", resuelve la ecuación asociada (esto implica encontrar los ceros de un polinomio)
• Etapa 4: Recoge todos los puntos críticos de la desigualdad, que en este caso son los ceros reales del auxiliar Ecuación polinómica (no consideras las raíces complejas en este caso)
• Paso 5: Si no existen puntos críticos, implica que la expresión no cambia de signo, por lo que toda la recta real será solución, o no, no hay solución. Para comprobarlo, elige cualquier punto y mira si satisface la desigualdad, y si lo hace, toda la recta real es la solución, si no, no hay solución
• Paso 6: Si hay puntos críticos, construya intervalos con puntos críticos consecutivos (usando -∞ como punto crítico inicial y ∞ como punto crítico final)
• Paso 7: Verifique cada uno de esos intervalos y vea si un punto dentro cumple con la desigualdad. Si es así, el intervalo es parte de la solución; si no, el intervalo no es parte de la solución.

La idea clave aquí es que los puntos críticos y los intervalos que derivamos de ellos son intervalos para los cuales la expresión no cambia de signo, por lo que o todo el intervalo es una solución o ningún punto del intervalo es parte de la solución.

Ceros polinomiales y puntos críticos

Una de las razones por las que es posible resolver desigualdades polinómicas es porque es relativamente sencillo analizar expresiones polinómicas en busca de puntos críticos, aparte del hecho de que los polinomios son expresiones continuas.

Habrá desigualdades como

\[\displaystyle \frac{\sin(x^2-1)}{x^3-1} < 1 \]

en el que será mucho más difícil encontrar puntos críticos. desigualdades lineales Es incluso más sencillo encontrar puntos críticos, pero eso es todo. Cualquier desigualdad general presentará sus propias complejidades.

Aplicaciones de polinomios en la vida real

Hay muchas aplicaciones de los polinomios. Por ejemplo, en Física, cuando estudias Cinemática, hay algunas expresiones polinómicas interesantes derivadas de las Leyes de Newton. Estas expresiones pueden definir condiciones para la posición de un cuerpo, lo que podría conducir a una desigualdad polinómica para determinar en qué momentos el cuerpo está por encima de cierta altura, lo que podría resultar crucial en balística, por ejemplo.

Además, al estudiar ecuaciones diferenciales, puedes encontrar términos dumpering en la ecuación que dependen de una potencia y tienen estructura polinomial, para lo cual puedes usar algunas desigualdades avanzadas, como las desigualdades de Gronwall.

Ejemplo: resolver desigualdades polinómicas

Resolver: \(x^2 - x > \frac{1}{2}\)

Solución: Primero debemos resolver la siguiente ecuación cuadrática \(\displaystyle x^2-x-\frac{1}{2}=0\):

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{1 \pm \sqrt{\left(-1\right)^2-4\left(1\right)\left(-\frac{1}{2}\right)}}{2\cdot 1} = \displaystyle \frac{1 \pm \sqrt{3}}{2}\]

entonces, encontramos que:

\[ {x}_1 = \frac{1}{2}-\frac{1}{2}\sqrt{3}=-\frac{1}{2}\sqrt{3}+\frac{1}{2} \] \[{x}_2 = \frac{1}{2}+\frac{1}{2}\sqrt{3}=\frac{1}{2}\sqrt{3}+\frac{1}{2}\]

Análisis de puntos críticos

La lista de puntos críticos encontrados organizados en orden ascendente es: \(-\frac{1}{2}\sqrt{3}+\frac{1}{2}\), \(\frac{1}{2}\sqrt{3}+\frac{1}{2}\).

En base a esto, debemos analizar los siguientes intervalos:

• Para el intervalo \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\): El lado izquierdo es positivo, entonces \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) es parte de la solución.

• Para el intervalo \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\): El lado izquierdo es negativo, lo que significa que \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) no es parte de la solución.

• Para el intervalo \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\): El lado izquierdo es positivo, lo que significa que \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\) es parte de la solución.

Solución a la desigualdad

Con base en la desigualdad proporcionada, y analizando los puntos críticos, encontramos que la solución a la desigualdad es: \(x < -\frac{1}{2}\sqrt{3}+\frac{1}{2}\) o \(x > \frac{1}{2}\sqrt{3}+\frac{1}{2}\).

Usando notación de intervalo, la solución se escribe como:

\[\left(-\infty,-\frac{1}{2}\sqrt{3}+\frac{1}{2}\right) \cup \left(\frac{1}{2}\sqrt{3}+\frac{1}{2},\infty\right)\]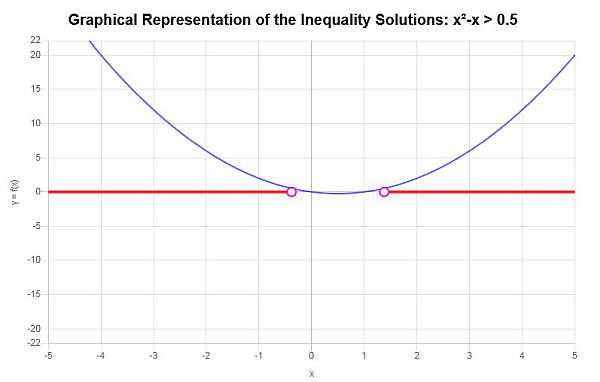

que concluye el cálculo.

Ejemplo: polinomio de grado superior

Resuelve la siguiente desigualdad: \(x^3 - x > 1\)

Solución:

Para resolver \(x^3-x > 1\) primero ponemos todo de un lado:

\[x^3-x-1> 0\]

Ahora, de esto obtenemos la ecuación asociada que debe resolverse primero, que es \(x^3-x-1=0\). Observe que el grado es \(\displaystyle deg(p) = 3\), su coeficiente principal es \(\displaystyle a_{3} = 1\) y su coeficiente constante es \(\displaystyle a_0 = -1\).

Intentando raíces racionales

Primero intentaremos encontrar raíces racionales simples, con el Teorema del cero racional.

La siguiente tarea es encontrar los números enteros que dividen el coeficiente principal \(a_{3}\) y el coeficiente constante \(a_0\), que se usarán para construir nuestros candidatos a ceros de la ecuación polinómica.

▹ Los divisores de \(a_{3} = 1\) son: \(\pm 1\).

▹ Los divisores de \(a_0 = -1\) son: \(\pm 1\).

Por lo tanto, dividiendo cada divisor del coeficiente constante \(a_0 = -1\) por cada divisor del coeficiente principal \(a_{3} = 1\), encontramos la siguiente lista de candidatos a ser raíces:

\[\pm \frac{ 1}{ 1}\]

Ahora, todos los candidatos necesitan ser probados para ver si son una solución. De la prueba de cada candidato se obtiene lo siguiente:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle -1^3-\left(-1\right)-1 & = & \displaystyle -1 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle 1^3-1-1 & = & \displaystyle -1 \ne 0 \\\\ \end{array}\]

Pero como no hemos encontrado raíces racionales por inspección, no podemos continuar con la factorización usando métodos elementales, por lo que el proceso se detiene aquí.

OPCIONAL : Este es un polinomio de grado \(3\), para el cual hay un total de raíces \(3\), aunque algunas pueden ser complejas, pero en este caso se han encontrado menos de \(3\) soluciones usando métodos elementales.

Utilizando métodos avanzados de ecuaciones cúbicas, se puede encontrar que el conjunto completo de soluciones es:

\[x_1=\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\]
\[x_2=\frac{\frac{1}{6}\cdot \left(-3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}+i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]
\[x_3=\frac{\frac{1}{6}\cdot \left(3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]

Análisis de puntos críticos

El único punto crítico que se encontró es \(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\).

En base a esto, debemos analizar los siguientes intervalos:

• Para el intervalo \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\): El lado izquierdo es negativo, por lo que \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\) no es parte de la solución.

• Para el intervalo \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\): El lado izquierdo es positivo, lo que implica que \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\) es parte de la solución.

Solución a la desigualdad

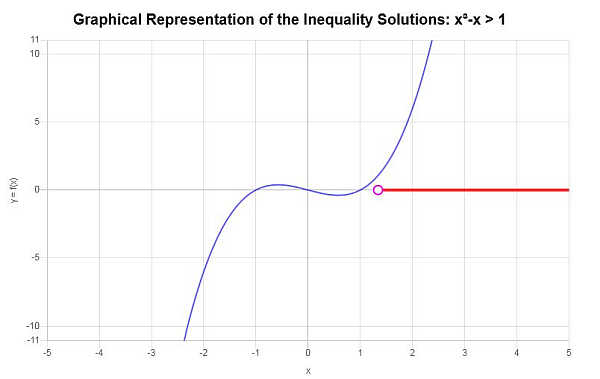
Con base en la desigualdad proporcionada, y analizando los puntos críticos, encontramos que la solución a la desigualdad es: \(x > 1.3247180451128\).

Usando notación de intervalo, la solución se escribe como:

\[\left(1.3247180451128,\infty\right)\]

Gráficamente:

Más calculadoras de desigualdad

Resolver desigualdades (prohibido encontrar soluciones a ecuaciones ) es una de las operaciones más comunes en matemáticas, en todos los ámbitos.

El proceso de resolución de desigualdades suele ser laborioso, y por lo general no existe una regla para solucionarlas. Resolver desigualdades polinomiales es una de las pocas excepciones, en la que podemos seguir una serie de pasos para encontrar las soluciones, pero aun así podemos fallar, porque los polinomios de mayor grado son difíciles de resolver. De hecho, es realmente imposible encontrar raíces polinómicas por encima del grado 5 usando una regla general (teorema de Abel).