Calculadora de desigualdad
Instrucciones: Utilice la calculadora de desigualdades para resolver cualquier desigualdad que proporcione, mostrando todos los pasos. Por favor escriba la desigualdad que desea resolver en el cuadro a continuación:
Más sobre cómo resolver desigualdades
Con esta calculadora podrás resolver desigualdades que te proporcionen. Todo lo que tienes que hacer es escribir la desigualdad que deseas en el cuadro y también asegurarte de que estás proporcionando una desigualdad válida.
Por ejemplo, podría proporcionar algo como '2x^2 - x >= 1/2', o algo como 'sin(x) > 0', siempre que proporcione valores válidos. También asegúrese de utilizar un signo de desigualdad, como ">", "<", ">=" o "<=".
Si en lugar de eso usas "=", entonces esta calculadora actuará como una calculadora de ecuaciones .
Una vez que proporciones una desigualdad válida, el siguiente paso es hacer clic en "Resolver", y en una fracción de segundo se te presentará la solución paso a paso. Una advertencia: no todas las desigualdades podrán resolverse, así que téngalo en cuenta.
No todas las desigualdades son fáciles de resolver ni podemos aplicar algunos métodos preconcebidos. Sólo algunos tipos, como desigualdades lineales , desigualdades cuadráticas o igualdades polinómicas (para grados inferiores) admitir un tratamiento sistemático.

¿qué es una desigualdad?
Una desigualdad es un tipo de objeto matemático que es muy similar a una ecuación matemática , con la diferencia de que en lugar de "=", una desigualdad contiene ">", "<", ">=" o "<=". Esta pequeña diferencia en apariencia aún agrega más complejidades a la resolución de una desigualdad que a una ecuación.
Por ejemplo, la siguiente expresión es una desigualdad
\[\displaystyle x + \frac{1}{3} < x^2 \]Entonces, es una expresión matemática que tiene dos lados, el lado izquierdo y el lado derecho, y tiene "<" como signo de desigualdad correspondiente. Se dice que la desigualdad anterior es una desigualdad cuadrática, porque las expresiones de los lados izquierdo y derecho son polinomiales y el grado más alto es 2.
Ahora, por ejemplo, la siguiente desigualdad es una desigualdad trigonométrica:
\[\displaystyle x + \frac{1}{3} \le \sin\left(x^2 + \frac{1}{x}\right) \]Es una desigualdad porque tiene el signo de desigualdad \(\le\) y el lado derecho contiene una expresión trigonométrica . Observe que la primera desigualdad es bastante sencilla de resolver, mientras que la otra desigualdad está lejos de ser fácil y, en realidad, no se puede resolver.
Cómo resolver una desigualdad
En términos generales, encontraremos la solución a las desigualdades resolviendo primero una ecuación asociada. Resolver la desigualdad será más difícil cuando la ecuación asociada sea más difícil de resolver. Los siguientes pasos le ayudarán en el proceso de solución:
- Paso 0: Simplifica las expresiones involucrados en la desigualdad. Casi siempre es más fácil resolver una desigualdad simplificada que resolver la original
- Paso 1: Identifique la desigualdad que desea resolver e identifique cuidadosamente el signo de desigualdad (>, ≥, <, ≤). Si tiene "=", entonces debería usar un calculadora de ecuaciones en cambio
- Paso 2: Luego escribe la ecuación asociada, que se obtiene simplemente reemplazando el signo de desigualdad encontrado en el paso anterior y luego reemplazándolo por el signo de igualdad "="
- Paso 3: Resuelve la ecuación asociada. Determinarás la solución de la desigualdad basándose en la existencia de soluciones reales a tu ecuación asociada y tomando notas sobre cualquier punto que pueda hacer que la expresión sea indefinida
- Etapa 4: Si su ecuación asociada no tiene una solución real: en ese caso, sabrá que la ecuación nunca es cero, al menos para valores reales. Entonces, y suponiendo continuidad, o todos los puntos son solución de la desigualdad o ninguno lo es. Entonces se evalúa la desigualdad en cualquier punto (digamos x = 0), y si se cumple, entonces todos los valores reales son solución a la desigualdad, y si no se cumple, entonces no hay soluciones reales
- Paso 5: Finalmente, supongamos que existen soluciones reales para la ecuación asociada. Llamaremos a esos puntos críticos y agregaremos cualquier punto donde la expresión deje de estar definida (divisiones por cero, etc.) a la lista de puntos críticos
- Paso 6: Si solo hay un punto crítico, al que llamamos 'a': Evalúe la desigualdad en cualquier punto a la izquierda de 'a' y, si se cumple, el intervalo (-∞, a) será parte del conjunto de soluciones. Si la desigualdad es "<=" o ">=", entonces incluyes el punto final. Finalmente, (-∞, a). Das un paso similar para un punto a la derecha de 'a', y si la desigualdad se cumple, entonces (-∞, a) será parte del conjunto de soluciones
- Paso 7: Se lleva a cabo un proceso similar si existe más de un punto crítico: Tome dos puntos críticos consecutivos, que llamamos 'a1' y 'a2': Evalúe la desigualdad en cualquier punto entre a1 y a2, y si se cumple, el intervalo ( a1, a2) serán parte del conjunto de solución. Si la desigualdad es "<=" o ">=", entonces incluyes los puntos finales
Parece complicado, pero sólo hay que ser sistemático. Por ejemplo, si su desigualdad es \(\displaystyle x + \frac{1}{3} < x^2 \), entonces la ecuación asociada es \(\displaystyle x + \frac{1}{3} = x^2 \), que es fácil de resolver, ya que es una Ecuación cuadrática .
Luego, en el contexto del análisis de los puntos críticos (si los hay), graficar la solución de la desigualdad puede aclarar las cosas. En algunas clases de Álgebra enseñan a los estudiantes a utilizar una tabulación para realizar un seguimiento de lo que sucede entre puntos críticos, lo que podría resultar realmente útil.
¿cuál es la diferencia con un sistema de desigualdades?
Un sistema de desigualdades consta de varias desigualdades simultáneas que deben resolverse al mismo tiempo. Suena más difícil que resolver una desigualdad simple porque es más difícil. Si resolver desigualdades puede resultar laborioso, más aún para los sistemas de desigualdades.
A continuación se muestra un ejemplo de un sistema de desigualdades:
\[\displaystyle x + y < 1 \] \[\displaystyle 2x + y^2 \le 1 \]En el ejemplo anterior tienes un sistema de desigualdades para ser resuelto. Este sistema de desigualdades tiene dos desigualdades y dos incógnitas (x e y).
Como probablemente puedas imaginar, resolver un sistema de desigualdades puede resultar difícil en general. Principalmente, nos centraremos en resolver sistemas de ecuaciones lineales, que están estrechamente relacionados con resolver un sistema de ecuaciones lineales

Ventajas de usar esta calculadora de desigualdades con pasos
Realmente, resolver la mayoría de las desigualdades será difícil. Sólo unos pocos seleccionados de ellos, con estructuras muy específicas, se prestarán a ser analizados. La mayoría no lo hará, así que será mejor que estés preparado para eso.
- Ventaja 1: Ahorre mucho tiempo: Resolver desigualdades puede llevar mucho tiempo, ya que primero debe resolver la ecuación asociada y luego analizar los puntos críticos
- Ventaja 2: Asegúrate de hacer lo mejor que puedas para resolverlo: como probablemente ya sepas, no todas las ecuaciones o desigualdades se pueden resolver fácilmente, o resolver en absoluto. Una calculadora con pasos intentará el mejor enfoque posible en función de la estructura detectada
- Ventaja 3: Obtenga resultados, paso a paso de forma ordenada. Algunas calculadoras te darán la respuesta final pero no mostrarán los pasos. Un gráfico que muestre las soluciones también será útil
Mientras aprende los entresijos, tener una calculadora de desigualdades que haga el trabajo pesado por usted le mostrará cómo se hacen las cosas y probablemente adquirirá las habilidades necesarias para detectar las estructuras que son más fáciles de abordar.
¿hay algún uso práctico para las desigualdades?
¡Puedes apostar! En matemáticas básicas (Álgebra y Cálculo 101), hay un mayor énfasis en igualdades y ecuaciones. El mundo real está lleno de procesos en los que no necesariamente tenemos ecuaciones, pero sí desigualdades que provienen de límites inferiores o superiores impuestos por algunas restricciones físicas.
Ciertos campos de matemáticas avanzadas, como las ecuaciones diferenciales, basan sus marcos teóricos en desigualdades (que a los expertos les gusta llamar "estimaciones de energía" en algunos contextos).
Puede que la importancia de las desigualdades no sea evidente para usted, ni la necesidad de aprenderlas demasiado urgente, pero verdaderamente, las desigualdades forman una de las piedras angulares de la metodología matemática utilizada para construir teorías, aunque en los bonitos resultados finales tendemos a ver igualdades. en cambio.

Ejemplo: resolver desigualdades
Calcula la solución a: \(\frac{1}{3}x + \frac{5}{4} \ge \frac{1}{6}\)
Solución: Necesitamos poner todos los términos de la desigualdad en el lado izquierdo (podría ser el lado derecho pero es bastante convencional usar el izquierdo):
\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6}\ge 0 \]De la desigualdad anterior, obtenemos la ecuación lineal asociada que debe resolverse primero:
\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6} = 0 \]Paso 0: En este caso, primero necesitamos simplificar la ecuación lineal dada y, para hacerlo, llevamos a cabo los siguientes pasos de simplificación:
Resolver la ecuación lineal
Poniendo \(x\) en el lado izquierdo y la constante en el lado derecho obtenemos
\[\displaystyle \frac{1}{3}x = -\frac{13}{12}\]Ahora, resolviendo \(x\), al dividir ambos lados de la ecuación entre \(\frac{1}{3}\), se obtiene lo siguiente
\[\displaystyle x = \displaystyle \frac{ -\frac{13}{12}}{ \frac{1}{3}}\]y simplificando obtenemos finalmente lo siguiente
\[\displaystyle x=-\frac{13}{4}\]Por lo tanto, resolver \(x\) para una ecuación lineal dada conduce a \(x=-\frac{13}{4}\).
Análisis de puntos críticos
El único punto crítico que se encontró es \(-\frac{13}{4}\).
En base a esto, debemos analizar los siguientes intervalos:
• Para el intervalo \(\left(-\infty, -\frac{13}{4}\right)\): El lado izquierdo es negativo, por lo que \(\left(-\infty, -\frac{13}{4}\right)\) no es parte de la solución.
• Para el intervalo \(\left(-\frac{13}{4}, \infty\right)\): El lado izquierdo es positivo, lo que significa que \(\left(-\frac{13}{4}, \infty\right)\) es parte de la solución.
Solución a la desigualdad
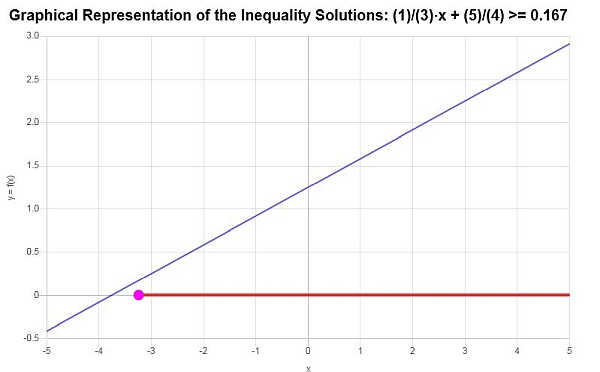
Con base en la desigualdad proporcionada, y analizando los puntos críticos, encontramos que la solución a la desigualdad es: \(x \ge -\frac{13}{4}\).
Usando notación de intervalo, la solución se escribe como:
\[\left[-\frac{13}{4},\infty\right)\]El gráfico de desigualdad lineal de la solución que se obtiene se muestra a continuación
Ejemplo: más ejemplos de desigualdad
Encuentre la solución de lo siguiente: \(\sin(x) > 0\)
Solución: Se nos da la siguiente desigualdad trigonométrica que debe resolverse:
\[\sin\left(x\right) > 0\]Manejo de una ecuación auxiliar
De la desigualdad trigonométrica anterior, obtenemos la ecuación asociada que debemos resolver primero:
\[\sin\left(x\right)=0\]Resolver la ecuación trigonométrica auxiliar
entonces las soluciones son: \(x = \pi{}K\), para una constante entera arbitraria \(K\).
Análisis de puntos críticos
Con base en las soluciones de la ecuación auxiliar, la lista de puntos críticos encontrada es: \(\pi{}K\), para una constante entera arbitraria \(K\).
Observa que tenemos una infinidad de intervalos críticos, por lo que analizamos algunos de ellos a continuación:
• Para el intervalo \(\left(-3\pi{}, -2\pi{}\right)\): El lado izquierdo es negativo, por lo que \(\left(-3\pi{}, -2\pi{}\right)\) no es parte de la solución.
• Para el intervalo \(\left(-2\pi{}, -\pi{}\right)\): El lado izquierdo es positivo, lo que significa que \(\left(-2\pi{}, -\pi{}\right)\) es parte de la solución.
• Para el intervalo \(\left(-\pi{}, 0\right)\): El lado izquierdo es negativo, lo que significa que \(\left(-\pi{}, 0\right)\) no es parte de la solución.
• Para el intervalo \(\left(0, \pi{}\right)\): El lado izquierdo es positivo, lo que significa que \(\left(0, \pi{}\right)\) es parte de la solución.
• Para el intervalo \(\left(\pi{}, 2\pi{}\right)\): El lado izquierdo es negativo, por lo que \(\left(\pi{}, 2\pi{}\right)\) no es parte de la solución.
• Para el intervalo \(\left(2\pi{}, 3\pi{}\right)\): El lado izquierdo es positivo, lo que significa que \(\left(2\pi{}, 3\pi{}\right)\) es parte de la solución.
Y así es como procedemos durante toda la secuencia de intervalos.
Intervalos de solución de piezas
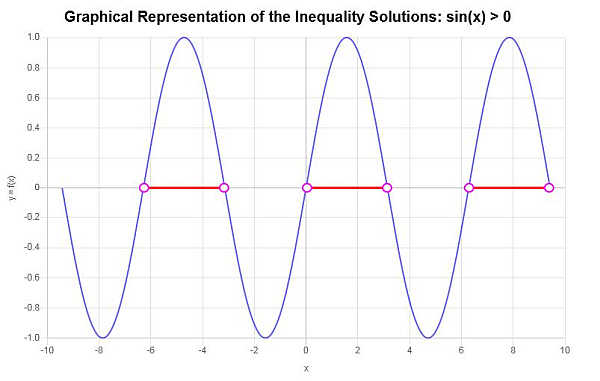
Con base en el análisis de los puntos críticos encontrados y los intervalos correspondientes generados por puntos críticos consecutivos, podemos identificar como parte de la solución a la desigualdad lo siguiente:
\[\left(-2\pi{}, -\pi{}\right) \cup \left(0, \pi{}\right) \cup \left(2\pi{}, 3\pi{}\right)\]En este caso, podemos identificar aproximadamente diferentes áreas de solución, como se muestra en el siguiente gráfico. El graficador de desigualdad produce la siguiente representación gráfica de la solución encontrada:
Ejemplo: más desigualdades
Resolver es la desigualdad cuadrática \( x^2 - 2x > 6 \).
Solución: La desigualdad que debemos resolver es
\[x^2-2x > 6\]Poniendo todos los términos de la desigualdad a un lado, obtenemos:
\[x^2-2x-6>0\]Ecuación auxiliar
Obtenemos la siguiente ecuación auxiliar, que primero debe resolverse:
\[x^2-2x-6=0\]Tenemos una expresión polinómica en el lado izquierdo, que es \(\displaystyle deg(p) = 2\), su coeficiente principal es \(\displaystyle a_{2} = 1\) y su coeficiente constante es \(\displaystyle a_0 = -6\).
Fórmula cuadrática
En este caso, las raíces se calculan mediante la siguiente fórmula:
\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\] \[\Rightarrow = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(1\right)\left(-6\right)}}{2\cdot 1} = \displaystyle \frac{2 \pm \sqrt{28}}{2}\]entonces, encontramos que:
\[ {x}_1 = \frac{2}{2}-\frac{1}{2}\sqrt{28}=\frac{2}{2}-\sqrt{7}=1-\sqrt{7}=-\sqrt{7}+1 \] \[{x}_2 = \frac{2}{2}+\frac{1}{2}\sqrt{28}=\frac{2}{2}+\sqrt{7}=1+\sqrt{7}=\sqrt{7}+1\]En este caso, la ecuación cuadrática \( \displaystyle x^2-2x-6 = 0 \), tiene dos raíces reales, las cuales se convierten en puntos críticos:
Análisis de puntos críticos
La lista de puntos críticos encontrados organizados en orden ascendente es: \(-\sqrt{7}+1\), \(\sqrt{7}+1\).
En base a esto, debemos analizar los siguientes intervalos:
• Para el intervalo \(\left(-\infty, -\sqrt{7}+1\right)\): El lado izquierdo es positivo, lo que implica que \(\left(-\infty, -\sqrt{7}+1\right)\) es parte de la solución.
• Para el intervalo \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\): El lado izquierdo es negativo, por lo que \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\) no es parte de la solución.
• Para el intervalo \(\left(\sqrt{7}+1, \infty\right)\): El lado izquierdo es positivo, lo que significa que \(\left(\sqrt{7}+1, \infty\right)\) es parte de la solución.
Encontrar la solución a la desigualdad
Con base en la desigualdad proporcionada, y analizando los puntos críticos, encontramos que la solución a la desigualdad es: \(x < -\sqrt{7}+1\) o \(x > \sqrt{7}+1\).
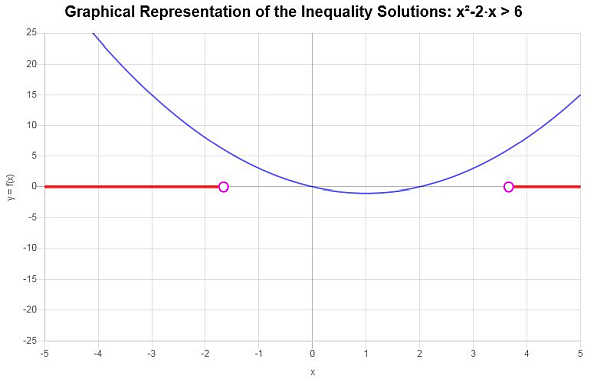
Usando notación de intervalo, la solución se escribe como:
\[\left(-\infty,-\sqrt{7}+1\right) \cup \left(\sqrt{7}+1,\infty\right)\]La solución de la desigualdad se muestra gráficamente:
Más sobre las desigualdades
Siempre empezarás con un calculadora de desigualdades lineales , o tal vez un calculadora de desigualdades cuadráticas , porque esos son los que garantizan una solución.
Entonces, incluso con un desigualdad polinómica podría estar topándose con arenas movedizas, ya que las desigualdades polinómicas también pueden volverse complicadas, o incluso imposibles de resolver exactamente con métodos elementales.
Cualquier otro tipo de desigualdad dependerá de su estructura y de alguna sustitución inteligente que se le ocurra.




