Más información sobre esta calculadora de desigualdad lineal

Esta calculadora le proporcionará las herramientas necesarias para abordar desigualdades lineales. En concreto podrás resolverlos y graficarlos, consiguiendo que se muestren todos los pasos.

Se permiten desigualdades lineales como '2x + 3 < 1' o '3x + 2y <=1' y luego, dependiendo del número de variables, obtendrás un gráfico adecuado junto con los pasos que conducen a la solución.

Una vez que se haya proporcionado una desigualdad lineal válida, todo lo que necesita hacer es hacer clic en "Resolver" para comenzar el proceso. Si falta algo o falta algo, la calculadora se lo informará.

Este tipo de desigualdades son las más simples que encontrarás y siempre son relativamente fáciles de resolver. Este tipo junto con desigualdades cuadráticas se encuentran entre las únicas desigualdades "fáciles" de resolver.

¿qué es una desigualdad lineal?

Una desigualdad lineal es el tipo más simple de desigualdad, en la que todos los términos involucrados son lineales o constantes.

\[\displaystyle a x + b y \le 1\]

Por ejemplo, la ecuación anterior es una ecuación lineal con dos variables. Técnicamente hablando, tenemos desigualdad polinómica de grado 1, pero esa es una forma demasiado complicada de verlo.

¿cómo se resuelve una desigualdad lineal?

• Paso 1: Pon todo lo que contenga la variable que quieres resolver en un lado y el resto en el otro
• Paso 2: grupo y simplifica la expresión , para reducir los términos semejantes
• Paso 3: Si una constante diferente a uno multiplica la variable que deseas resolver, divídela por ella. Una advertencia: si divides por un valor negativo, necesitas cambiar la dirección de la desigualdad

Uno de los principales puntos a tener en cuenta, y que diferencian los procesos de resolución de ecuaciones y desigualdades, es que al resolver ecuaciones podemos multiplicar (o dividir) más libremente por constantes y nada cambia, mientras que con las desigualdades debemos tener más cuidado, ya que multiplicar (o dividir) por constantes negativas cambia la dirección de la desigualdad.

¿cuál es la desigualdad lineal más general?

Lo más general que puedes conseguir con lineal es

\[\displaystyle a x + bx \le c\]

pero aun así puedes tener '<' en lugar de '\(\le\)'. O podríamos haber

\[\displaystyle a x + bx \ge c\]

pero también puedes usar '>' en lugar de '\(\ge\)'.

Similar a lo que sucedió con la suma y la resta, la división de fracciones se deriva simplemente de la multiplicación de fracciones: para dividir dos fracciones, simplemente se multiplica la primera por la fracción inversa de la segunda (la fracción inversa se obtiene intercambiando el numerador por el denominador en la fracción).

Aplicaciones

Las desigualdades lineales encuentran muchas aplicaciones en matemáticas. Una desigualdad lineal es un tipo de promedio ponderado, muy adecuado para todo tipo de problemas de mezcla y asignación.

Cuando se tratan problemas escritos, normalmente se encuentran ecuaciones lineales, pero no es inusual tener que lidiar también con desigualdades lineales.

Una de las áreas más conocidas es la Optimización y Programación Lineal, en la que las desigualdades lineales juegan un papel crucial, tanto con el método Simplex como con las condiciones de Kuhn-Tucker cuando se trata de una función objetivo no lineal.

Ejemplo: resolver desigualdades

Resuelve la siguiente desigualdad lineal: \(\frac{2}{3} x + \frac{5}{4} < - \frac{1}{6}\)

Solución:

Necesitamos poner todos los términos de la desigualdad a un lado:

\[\frac{2}{3}x+\frac{5}{4}- \left(-\frac{1}{6}\right)< 0\]

Ecuación auxiliar asociada

Necesitamos resolver:

\[\frac{2}{3}x+\frac{5}{4}-\left(-\frac{1}{6}\right)=0\]

Paso 0: En este caso, primero necesitamos simplificar la ecuación lineal dada y, para hacerlo, llevamos a cabo los siguientes pasos de simplificación:

Resolver la ecuación lineal

Poniendo \(x\) en el lado izquierdo y la constante en el lado derecho obtenemos

\[\displaystyle \frac{2}{3}x = -\frac{17}{12}\]

Ahora, resolviendo \(x\), al dividir ambos lados de la ecuación entre \(\frac{2}{3}\), se obtiene lo siguiente

\[\displaystyle x = \displaystyle \frac{ -\frac{17}{12}}{ \frac{2}{3}}\]

y simplificando obtenemos finalmente lo siguiente

\[\displaystyle x=-\frac{17}{8}\]

Por lo tanto, resolver \(x\) para una ecuación lineal dada conduce a \(x=-\frac{17}{8}\).

Puntos críticos

Como es de esperarse para una desigualdad lineal, solo existe un punto crítico, que es \(-\frac{17}{8}\), a partir del cual analizamos los siguientes intervalos:

• Para el intervalo \(\left(-\infty, -\frac{17}{8}\right)\): El lado izquierdo es negativo, lo que significa que \(\left(-\infty, -\frac{17}{8}\right)\) es parte de la solución.

• Para el intervalo \(\left(-\frac{17}{8}, \infty\right)\): El lado izquierdo es positivo, lo que implica que \(\left(-\frac{17}{8}, \infty\right)\) no es parte de la solución.

Solución a la desigualdad

Por tanto, se encuentra que la solución a la desigualdad es: \(x < -\frac{17}{8}\).

La expresión la solución con notación de intervalo, la solución se escribe como:

\[\left(-\infty,-\frac{17}{8}\right)\]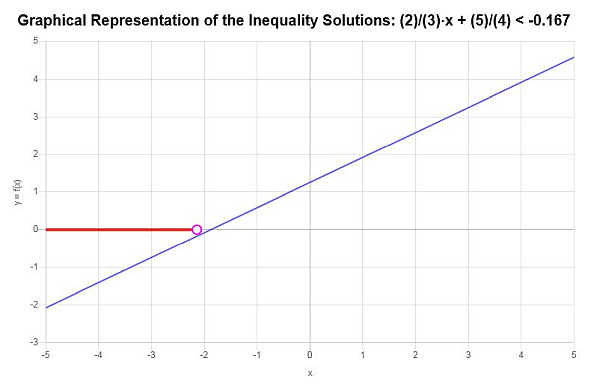

Ejemplo: más desigualdades lineales

Resuelve esta desigualdad lineal de 2 variables: \(\frac{1}{3} x + \frac{5}{4} y < - \frac{5}{6}\)

Solución:

Necesitamos resolver:

\[\frac{1}{3}x+\frac{5}{4}y < -\frac{5}{6}\]

Tenemos una desigualdad lineal dada y necesitamos resolver la variable \(y\).

En este caso, resolvemos para \(y\), por lo que poniéndolo en un lado de la desigualdad y el resto en el otro lado obtenemos:

\[\frac{5}{4}y<-\frac{1}{3}x-\frac{5}{6}\]

Para resolver \(y\), dividimos ambos lados de la desigualdad entre \(\frac{5}{4}\) y finalmente obtenemos:

\[y < -\frac{4}{15}x-\frac{2}{3}\]

Solución de desigualdad lineal

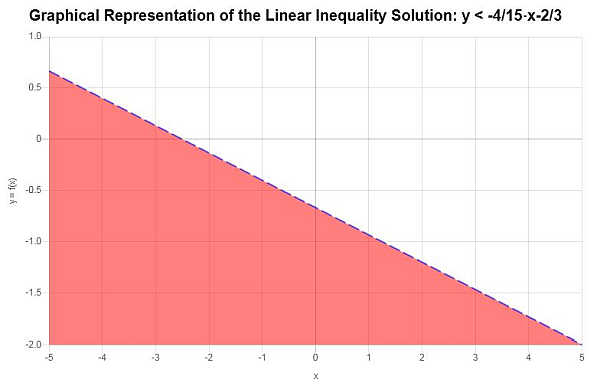
Según la desigualdad proporcionada, después de resolverla para \(y\) obtenemos:

\[y < -\frac{4}{15}x-\frac{2}{3}\]

La representación gráfica de la región de solución se muestra en el siguiente gráfico:

Más calculadoras de álgebra

Tratar con la expresión es crucial en Álgebra. Simplificación de expresiones es el comienzo de la mayoría de los procesos matemáticos y, por lo general, es necesario reducir las cosas a su expresión más simple.

Resolver ecuaciones y también Resolver desigualdades permanecerá en el centro de la mayoría de los procesos, ya que uno u otro estará en el centro de casi todo lo que hagas en Matemáticas.