Más sobre desigualdades cuadráticas

Este cálculo de desigualdad cuadrática le proporcionará soluciones a desigualdades que muestran todos los pasos. Por ejemplo, la desigualdad que proporcionas puede ser algo así como 'x^2 - 1/2 > 0' y, en general, las desigualdades cuadráticas no son demasiado difíciles de resolver.

Una vez que proporcionas una desigualdad válida que involucra expresión cuadrática , puede hacer clic en "Calcular" para que se le muestren todos los pasos del cálculo, incluido un gráfico de las soluciones de desigualdad.

desigualdades cuadráticas son uno de los pocos tipos (junto con desigualdades lineales ) que tienes la garantía de poder encontrar una solución exacta, y este proceso implica resolver una ecuación cuadrática.

¿cuál es la definición de este tipo de desigualdad?

No lo hemos dicho explícitamente, pero queda bastante claro por su nombre: una desigualdad cuadrática es un tipo específico de desigualdad en la que todos los términos involucrados en ella son polinomios de como máximo grado 2. En este contexto, un ejemplo es

\[\displaystyle x^2 < x - 1\]

que es cuadrática por el hecho de que ambos lados de la desigualdad son polinomios de orden como máximo 2. Ahora, si tuvieras:

\[\displaystyle x^2 < x^3 - 1\]

entonces la desigualdad ya no es cuadrática debido al término \(x^3\) en el lado derecho. Para estas desigualdades tenemos una hoja de ruta clara para encontrar la solución.

Pasos para resolver desigualdades cuadráticas

• Paso 1: Asegúrate de tener una desigualdad cuadrática, ya que el método utilizado en este caso es válido solo para este tipo de desigualdad
• Paso 2: Como ocurre con la mayoría de las desigualdades, pasa todo al lado izquierdo de la desigualdad y resuelve la ecuación asociada
• Paso 3: Si la ecuación cuadrática asociada no tiene raíces reales, entonces sabemos que o toda la recta real es una solución o no hay solución. Entonces prueba cualquier punto y ve si resuelve la desigualdad, y si lo hace, la solución es la recta real completa (-∞, ∞); de lo contrario, la solución está vacía.
• Etapa 4: Si la ecuación cuadrática asociada tiene solo una solución real, significa que la gráfica cuadrática asociada toca tangencialmente el eje x. Entonces, dependiendo del signo de desigualdad, es posible que solo el punto de contacto sea la solución, o que todo excepto el punto de contacto sea la solución, o toda la línea real (-∞, ∞), para lo cual necesita probar el punto de contacto, y un punto fuera de eso (a la izquierda y a la derecha del punto)
• Etapa 4: Si la ecuación cuadrática asociada tiene dos soluciones reales diferentes, verifica los intervalos definidos por estas raíces para determinar qué partes de la recta real formarán parte de la solución

Una vez que analizas las piezas, si es necesario, las unes utilizando el operador de "unión", que se utiliza para unir intervalos.

¿cómo se dibuja una desigualdad cuadrática?

Graficar desigualdades proporciona una excelente manera de comprender visualmente cómo se ve la solución. En términos del procedimiento, necesitas saber si estás trabajando con una desigualdad de una variable o si tienes más variables.

Si tienes una desigualdad como

\[\displaystyle x^2 - \frac{1}{2} x < 1 \]

solo tienes una variable y entonces la solución será un subconjunto de la línea real. Por otro lado, si tuvieras algo como

\[\displaystyle y < x^2 - \frac{1}{2} x \]

entonces tienes solo dos variables xey, y entonces la solución de la desigualdad será un subconjunto del plano xy.

Importancia de las expresiones cuadráticas

Las expresiones cuadráticas involucradas en ecuaciones y desigualdades juegan un papel fundamental en Matemáticas. Quizás, la cuadrática sea el tipo de estructura más utilizado después de la lineal.

Cuando se trata de Cálculo y Álgebra, encontrará innumerables aplicaciones de cuadráticas en problemas de maximización y minimización, integración y mucho más. Indagando un poco encontrarás aplicaciones de expresiones cuadráticas en diferentes disciplinas científicas

Ejemplo: desigualdades cuadráticas

Resuelve esta desigualdad cuadrática: \(\frac{1}{3}x^2 + \frac{5}{4}x - \frac{5}{6} < 0\)

Solución:

Primero debemos resolver la siguiente ecuación cuadrática auxiliar \(\displaystyle \frac{1}{3}x^2+\frac{5}{4}x-\frac{5}{6}=0\).

Aplicando la fórmula cuadrática

La ecuación cuadrática es:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

En este caso tenemos:

\[a = \frac{1}{3}\] \[b = \frac{5}{4}\] \[c = -\frac{5}{6}\]

Introduciendo estos valores en la fórmula de las raíces obtenemos:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\left(\frac{5}{4}\right)^2-4\left(\frac{1}{3}\right)\left(-\frac{5}{6}\right)}}{2\cdot \frac{1}{3}} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\frac{385}{144}}}{\frac{2}{3}}\]

entonces, encontramos que:

\[ {x}_1 = -\frac{\frac{5}{4}}{\frac{2}{3}}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{-5\cdot 3}{4\cdot 2}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{15}{8}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{1}{8}\sqrt{385}-\frac{15}{8} \] \[{x}_2 = -\frac{\frac{5}{4}}{\frac{2}{3}}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{-5\cdot 3}{4\cdot 2}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{15}{8}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{1}{8}\sqrt{385}-\frac{15}{8}\]

Puntos críticos

La lista de puntos críticos encontrados organizados en orden ascendente es: \(-\frac{1}{8}\sqrt{385}-\frac{15}{8}\), \(\frac{1}{8}\sqrt{385}-\frac{15}{8}\).

Entonces, necesitamos analizar los siguientes intervalos críticos:

• Para el intervalo \(\left(-\infty, -\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\): El lado izquierdo es positivo, por lo que \(\left(-\infty, -\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) no forma parte de la solución.

• Para el intervalo \(\left(-\frac{1}{8}\sqrt{385}-\frac{15}{8}, \frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\): El lado izquierdo es negativo, lo que implica que \(\left(-\frac{1}{8}\sqrt{385}-\frac{15}{8}, \frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) es parte de la solución.

• Para el intervalo \(\left(\frac{1}{8}\sqrt{385}-\frac{15}{8}, \infty\right)\): El lado izquierdo es positivo, lo que significa que \(\left(\frac{1}{8}\sqrt{385}-\frac{15}{8}, \infty\right)\) no es parte de la solución.

Solución

Con base en la desigualdad proporcionada, y analizando los puntos críticos, encontramos que la solución a la desigualdad es: \(-\frac{1}{8}\sqrt{385}-\frac{15}{8}< x \le \frac{1}{8}\sqrt{385}-\frac{15}{8}\).

Usando notación de intervalo, la solución se escribe como:

\[\left[-\frac{1}{8}\sqrt{385}-\frac{15}{8},\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\]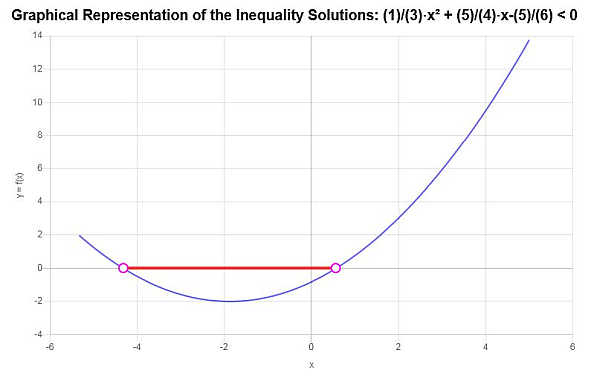

Ejemplo: más desigualdades cuadráticas

Resolver: \(x^2 < 4\)

Solución:

La desigualdad dada es:

\[x^2 < 4\]

que deriva a la ecuación cuadrática \(\displaystyle x^2-4=0\).

Fórmula cuadrática

Para una ecuación cuadrática de la forma \(a x^2 + bx + c = 0\), las raíces se calculan usando la siguiente Fórmula cuadrática :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

En este caso, tenemos que la ecuación que necesitamos resolver es \(\displaystyle x^2-4 = 0\), lo que implica que los coeficientes correspondientes son:

\[a = 1\] \[b = 0\] \[c = -4\]

Primero, calcularemos el discriminante para evaluar la naturaleza de las raíces. La discriminación se calcula como:

\[\Delta = b^2 - 4ac = \displaystyle \left( 0\right)^2 - 4 \cdot \left(1\right)\cdot \left(-4\right) = 16\]

Como en este caso obtenemos que el discriminante es \(\Delta = \displaystyle 16 > 0\), que es positivo, sabemos que la ecuación tiene dos raíces reales diferentes.

Ahora, reemplazando estos valores en la fórmula de las raíces obtenemos:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{0 \pm \sqrt{\left(0\right)^2-4\left(1\right)\left(-4\right)}}{2\cdot 1} = \displaystyle \frac{0 \pm \sqrt{16}}{2}\]

entonces, encontramos que:

\[ {x}_1 = \frac{0}{2}-\frac{1}{2}\sqrt{16}=\frac{0}{2}-2\cdot 1=\frac{0}{2}-2=-2 \] \[{x}_2 = \frac{0}{2}+\frac{1}{2}\sqrt{16}=\frac{0}{2}+2\cdot 1=\frac{0}{2}+2=2\]

En este caso, la ecuación cuadrática \( \displaystyle x^2-4 = 0 \), tiene dos raíces reales, entonces:

\[\displaystyle x^2-4 = \left(x+2\right)\left(x-2\right)\]

entonces el polinomio original se factoriza como \(\displaystyle p(x) = x^2-4 = \left(x+2\right)\left(x-2\right) \), lo que completa la factorización.

Análisis de puntos críticos

La lista de puntos críticos encontrados organizados en orden ascendente es: \(-2\), \(2\).

En base a esto, debemos analizar los siguientes intervalos:

• Para el intervalo \(\left(-\infty, -2\right)\): El lado izquierdo es positivo, por lo que \(\left(-\infty, -2\right)\) no forma parte de la solución.

• Para el intervalo \(\left(-2, 2\right)\): El lado izquierdo es negativo, entonces \(\left(-2, 2\right)\) es parte de la solución.

• Para el intervalo \(\left(2, \infty\right)\): El lado izquierdo es positivo, lo que significa que \(\left(2, \infty\right)\) no es parte de la solución.

Solución a la desigualdad

Con base en la desigualdad proporcionada, y analizando los puntos críticos, encontramos que la solución a la desigualdad es: \(-2< x \le 2\).

Usando notación de intervalo, la solución se escribe como:

\[\left[-2,2\right)\]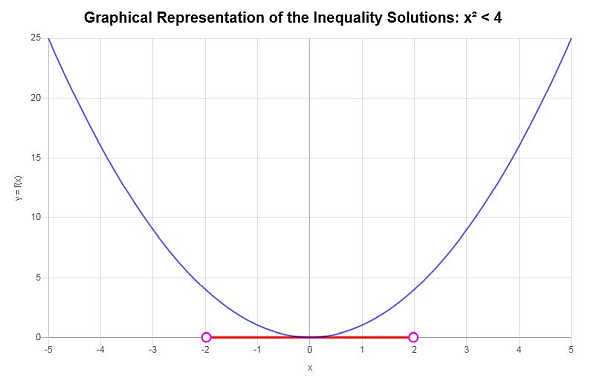

Otras calculadoras de desigualdad útiles

El tipo de desigualdad más simple que podrás resolver es desigualdades lineales . Después de eso, tienes desigualdades cuadráticas, en términos de facilidad.

Entonces tiene desigualdades polinomiales en general, con un grado superior a 2. Deberían ser sencillas, pero aún así podrían ser tareas formidables en términos de la cantidad de trabajo laborioso requerido para resolverlas.

tener un calculadora de desigualdad para las desigualdades en general puede resultar realmente útil, ya que abordará los diferentes tipos de desigualdades que son susceptibles de buscar soluciones exactas.