Linearer näherungsrechner

Diese linearisierungsrechner ermöglicht die Berechnung der linearen Annäherung, auch bekannt als Tangente für eine bestimmte gültige Funktion zu einem bestimmten gültigen Punkt.

Sie müssen eine gültige Funktion angeben, z. B. f(x) = x*sin(x) oder f(x) = x^2 - 2x + 1 oder eine beliebige gültige Funktion, die differenzierbar ist, und einen Punkt \(x_0\), an dem die Funktion gut definiert ist. Dieser Punkt kann ein beliebiger gültiger numerischer Ausdruck sein, z. B. 1/3.

Sobald Sie eine gültige Funktion und einen gültigen Punkt angegeben haben, klicken Sie auf "Berechnen" und alle Berechnungen werden für Sie angezeigt.

Bei der linearen Annäherung oder Annäherung erster Ordnung wird eine Annäherung der gegebenen Funktion durch eine Linie an einem bestimmten Punkt \(x_0\) gesucht. Bei Kurven ist eine lineare Approximation natürlich nur grob, aber der Grundgedanke ist, dass die Approximation für Punkte in der Nähe von \(x_0\) genau ist.

Lineare näherung

Es geht darum, eine Linie zu finden, die durch den Punkt \((x_0, f(x_0))\) verläuft und die Funktion \(f(x)\) "kaum berührt". Die formale mathematische Definition von "kaum berühren" wird durch die Idee von Tangente , für die wir müssen Berechnen sie Dasivat der Funktion.

Die Formel für die lineare Annäherung im Punkt \(x_0\) hängt nämlich von der Ableitung \(f'(x_0)\) ab, und zwar wie folgt

\[\displaystyle y = f(x_0) + f'(x_0) (x - x_0) \]

Diese lineare Näherungsformel definiert im Wesentlichen die Gleichung einer Linie die durch den Punkt \((x_0, f(x_0))\) verläuft, weshalb sie als "lineare Approximation" bezeichnet wird, da sie eine lineare Funktion definiert, die im Punkt \(x_0\) mit \(f(x)\) übereinstimmt und für Werte von \(x\), die nahe an \(x_0\) liegen, sehr nahe an \(f(x)\) liegt.

Schritte zum auffinden der linearen näherung

• Schritt 1: Sie müssen eine bestimmte Funktion F (x) und einen Punkt x0 haben.Die Funktion muss bei x0 differenzierbar sein
• Schritt 2: Berechnen Sie F (x0) und f '(x0), die die Funktion und Ableitung der Funktion F am Punkt x0 sind
• Schritt 3: Definieren Sie die lineare Approximation als y = f(x_0) + f'(x_0) (x - x_0), was der oben dargestellten Linearisierungsformel entspricht

Diese Linie, \(y = f(x_0) + f'(x_0) (x - x_0)\), stellt die Annäherung erster Ordnung dar, die auch als lokale lineare Annäherung bezeichnet wird.

Link mit tangentiallinie

Wie Sie wahrscheinlich inzwischen vermutet haben, ist die lineare Näherung dieselbe wie die Tangente am angegebenen Punkt.Die Berechnung der linearen Näherung ist dann genau das gleiche wie die Berechnung der Tangentenlinie

Ein anderer Name für diese Methode ist Annäherung erster Ordnung oder Annäherung an die Tangente, die auch in der Infinitesimalrechnung gebräuchliche Bezeichnungen sind.

Differential- und lineare annäherung

Ein weiteres gängiges Konzept ist das des Differentials, das eng mit dem der linearen Annäherung verbunden ist und einfach eine Ableitung davon ist. Das Differential (oder die endliche Differenz) ist nämlich definiert als \(\Delta y = y - f(x_0)\). Ausgehend von der Näherungsformel erster Ordnung lautet die Formel für das Differential also

\[\displaystyle \Delta y = y - f(x_0) = f'(x_0) (x - x_0) = f'(x_0) \Delta x \]

Das sieht natürlich genauso aus wie die lineare Näherungsformel, nur dass der Term \(f(x_0\) nach links weitergereicht wird.

Beispiel: berechnung der näherung erster ordnung.

Betrachten Sie das Folgende: \(f(x) = x^2 - 2x + 3\), finde seine Näherung erster Ordnung bei \(x_0 = 1\).

Lösung: Die Funktion, die uns zur Verfügung gestellt wurde, ist \(\displaystyle f(x)=x^2-2x+3\), und wir müssen die lineare Annäherung um den Punkt x = 1 finden. Wir brauchen also zunächst die Ableitung.

Lineare Nähung : Die Gleichung für die lineare Annäherung, die wir für den Punkt \(x_0 = 2\) suchen, ergibt sich aus der folgenden Formel

\[y = y_0 + f'(x_0)(x - x_0) \]

Beachten Sie, dass nach der Definition \(\displaystyle y_0 = f(x_0)\), die impliziert, dass wir brauchen, um die Funktion an der Stelle \(x_0 = 2\) stecken:

\[y_0 = f(x_0) = f\left(2\right) = 2^2-2\cdot 2+3 = 3\]

Wir machen das Gleiche, aber jetzt für die Ableitung am Punkt \(x_0 = 2\), also dann

\[f'(x_0) = f'\left(2\right) = 2\cdot 2-2 = 2 \]

Jetzt kehren wir zur linearen Annäherungsformel zurück:

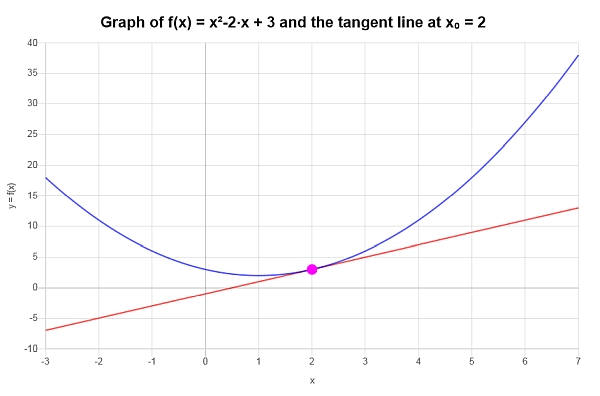
\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 3+2\left(x-2\right) = 2x-1 \]

Schlussfolgerung : Wir folgern, dass die lineare Approximation für \(\displaystyle f(x)=x^2-2x+3\) bei \(x_0 = 2\) gegeben ist durch:

\[y = 2x-1 \]

Grafisch:

Beispiel: weitere annäherung erster ordnung

Für die Funktion : \(f(x) = x \sin(x)\) und den Punkt \(x_0 = 2\) finden Sie die entsprechende Näherung erster Ordnung.

Lösung: In diesem Fall ist die Funktion, mit der wir arbeiten müssen: \(\displaystyle f(x)=x\sin\left(x\right)\).

Wir berechnen nun sein Derivat:

Lineare Nähung : Die Gleichung der linearen Näherung lautet:

\[y = y_0 + f'(x_0)(x - x_0) \]

wobei \(\displaystyle y_0 = f(x_0)\), so dann berechnen wir:

\[y_0 = f(x_0) = f\left(2\right) = 2\sin\left(2\right)\]

Für die Ableitung bei \(x_0 = 2\) stellen wir fest, dass:

\[f'(x_0) = f'\left(2\right) = 2\cos\left(2\right)+\sin\left(2\right) \]

Jetzt sind wir bereit, diese wieder in die Annäherungsformel der ersten Ordnung zu bringen:

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 2\sin\left(2\right)+2\cos\left(2\right)+\sin\left(2\right)\left(x-2\right) = 2x\cos\left(2\right)+x\sin\left(2\right)-4\cos\left(2\right) \]

Schlussfolgerung : Es wird festgestellt, dass die lineare Annäherung von \(\displaystyle f(x)=x\sin\left(x\right)\) an den gegebenen Punkt \(x_0 = 2\) wie folgt berechnet wird:

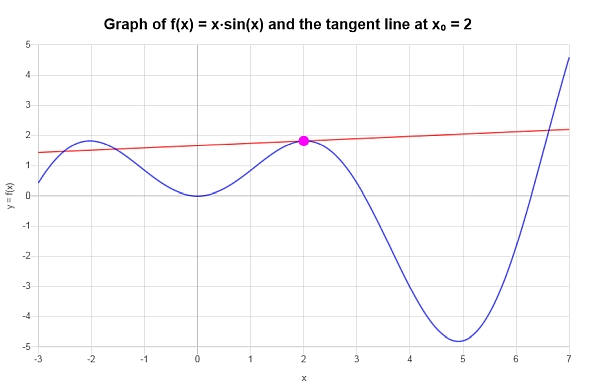
\[y = 2x\cos\left(2\right)+x\sin\left(2\right)-4\cos\left(2\right) \]

Grafisch erhalten wir das folgende Diagramm:

Beispiel: lineare annäherungsberechnung

Berechnen Sie die Approximation erster Ordnung für \( f(x) = \frac{\sin(x)}{x}\) bei \(x = \frac{\pi}{4}\).

Lösung: Die folgende Funktion wurde bereitgestellt: \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), für die wir ihre Ableitung berechnen müssen.

Die Funktion wurde bereits vereinfacht, sodass wir direkt sein Ableitungsbereich berechnen können:

Annauerung Erster Ordnung : Die Gleichung für die entsprechende Approximation erster Ordnung für die gegebene Funktion \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\) am gegebenen Punkt \(x_0 = \frac{\pi}{4}\) ist wie folgt gegeben:

\[y = y_0 + f'(x_0)(x - x_0) \]

Steckung der entsprechenden Werte:

\[y_0 = f(x_0) = f\left(\frac{\pi}{4}\right) = \frac{\sin\left(\frac{\pi{}}{4}\right)}{\frac{\pi{}}{4}} = \frac{2\sqrt{2}}{\pi{}}\] \[f'(x_0) = f'\left(\frac{\pi}{4}\right) = \frac{\cos\left(\frac{\pi{}}{4}\right)}{\frac{\pi{}}{4}}-\frac{\sin\left(\frac{\pi{}}{4}\right)}{\left(\frac{\pi{}}{4}\right)^2} = \frac{2\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}}{\pi{}^2} \]

Jetzt können wir dies also in die Formel einfügen:

\[y = y_0 + f'(x_0)(x - x_0) \] \[\Rightarrow y = \frac{2\sqrt{2}}{\pi{}}+\frac{2\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}}{\pi{}^2}\left(x-\frac{1}{4}\pi{}\right) = -\frac{1}{2}\sqrt{2}+\frac{2\sqrt{2}x}{\pi{}}+\frac{4\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}x}{\pi{}^2} \]

Schlussfolgerung : Daraus lässt sich schließen, dass die Näherung erster Ordnung für die gegebene Funktion \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\) an dem gegebenen Punkt \(x_0 = \frac{\pi}{4}\) gegeben ist durch

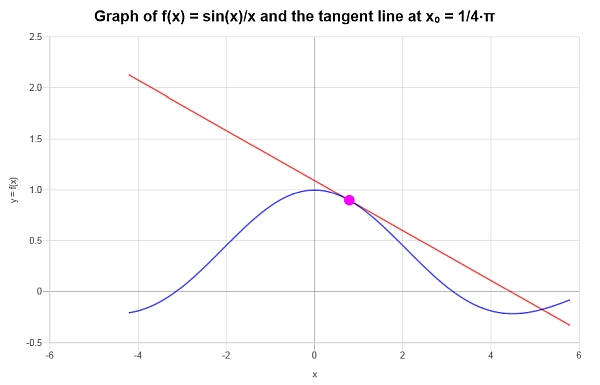
\[y = -\frac{1}{2}\sqrt{2}+\frac{2\sqrt{2}x}{\pi{}}+\frac{4\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}x}{\pi{}^2} \]

Das Folgende wird grafisch erhalten:

Weitere derivaterechner

Abgesehen davon linearisierungsrechner können Sie eine Menge finden, die verschiedene Dinge auf der Grundlage von Ableitungen tun. Die Differenzierung ist eine wichtige Operation in der Kalkulation, der Physik, dem Ingenieurwesen und der Wirtschaft mit einem breiten Spektrum von Anwendungen.

Es gibt auch eine Möglichkeit, eine lineare Annäherung für mehrere Variablen durchzuführen, z. B. für eine Funktion \f(x, y)\), in diesem Fall wird die lineare Annäherungsformel zu \(f(x, y) = f(x_0, y_0) + \frac{\partial f}{\partial x}(x_0, y_0)(x-x_0) + \frac{\partial f}{\partial y}(x_0, y_0)(y-y_0)\), so dass wir in diesem Fall, um die Linearisierung zu finden, Folgendes verwenden müssen Telableitungen .

Die Suche nach der Linearisierung einer Funktion ist bei weitem nicht das Einzige, was man mit Ableitungen machen kann. Die Differenzierung ist eine relativ einfache Operation mit einfachen Regeln wie der Produktregel , Die quotienteregel und die Kettenregel Dadurch wird die Berechnung von Derivaten zu einem relativ einfachen Betrieb.

Obwohl es einfach sein soll, ist es eine gute Idee, a zu verwenden Derivatnetisch um alle Schritte mit einer klaren Erwähnung von allen zu erwähnen Fähigkeitsregeln gebraucht.