Differentialrechner
Anweisungen: Verwenden Sie diesen Differentialrechner, um das Differential einer von Ihnen bereitgestellten Funktion zu ermitteln, an einem bestimmten Punkt, den Sie bereitstellen, alle Schritte anzuzeigen.Bitte geben Sie die Funktion und den Punkt im folgenden Formularfeld ein.
Differentialrechner
Mit diesem Taschenrechner können Sie das Differential einer von Ihnen bereitgestellten Funktion berechnen, an einem Punkt, den Sie bereitstellen, alle Schritte des Prozesses anzuzeigen.
Die Funktion, die Sie bereitstellen, kann eine gültige differenzierbare Funktion wie f (x) = x^2 + 2x oder f (x) = x^2*sin (x) sein, nur um zwei Beispiele zu erwähnen.
Wenn Sie dann die Funktion und den Punkt für die unterschiedliche Berechnung bereitgestellt haben, klicken Sie einfach auf "Berechnen", um alle Schritte des angezeigten Prozesses zu erhalten.
Die Idee von Differential ist fest mit dem der Tangentenlinie und Lineare Nähung , wie das Differential genau die Variation von Y entlang der messen Tangente am angegebenen Punkt.
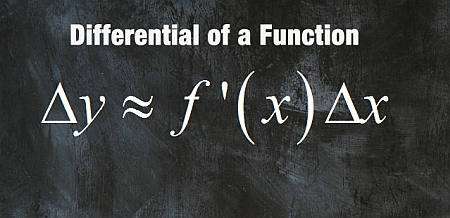
Was ist ein differential?
In der Differentialrechnung ist die Idee, dass Ableitungen Ihnen Informationen über die sofortige Änderungsrate einer Funktion an einem bestimmten Punkt liefern.
Das Konzept der Differential verwendet die Änderungsrate bestimmt durch die Ableitung an einem bestimmten Punkt \(x_0\), um das Verhalten der Funktion durch ihre zu approximieren Tangente .
Die Formel des Differentials basiert auf der Idee, dass
\[\displaystyle \Delta y \approx f'(x_0) \Delta x \]wo \(\Delta y = y - f(x_0)\) und \(\Delta x = x - x_0\).Für das Differential \(dy\) definieren wir
\[\displaystyle dy = f'(x_0) dx \]Diese (lose) Definition basiert auf der Idee, dass die lineare Annäherung und der Funktionsansatz für das gleiche Verhalten, wenn \(x\) an \(x_0\) nahezu nahezu ist.
Schritte zum berechnen eines differentials
- Schritt 1: Identifizieren Sie die Funktion f (x) und den Punkt x0, bei dem Sie das Differential berechnen möchten
- Schritt 2: Berechnen Sie das Derivat f '(x) und bewerten Sie es bei x0, damit Sie f' (x0) bekommen.Vereinfachen Sie es bei Bedarf
- Schritt 3: Verwenden Sie die Formel \(\displaystyle dy = f'(x_0) dx \)
Manchmal finden Sie das als \(\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \) geschriebene Differential, um anzuzeigen, dass Sie das Differential verwenden, um Änderungen in y zu schätzen, gemessen mit \(\Delta y\).
Differentialrechner dy
Verwendung einer Differentialrechner Kann Ihnen Zeit sparen, wenn Sie den Ableitungsberechnungsprozess berechnen.Die Idee des Unterschieds war schon immer seltsam, in dem Sinne, dass es lose definiert zu sein scheint.
Obwohl es eine Möglichkeit gibt, Unterschiede und ihre Operationen formell zu definieren (ein Subjekt, das als Differentialformen bezeichnet)Nicht zur Verfügung stellen.
Gesamtdifferenzinterpretation
Die häufigste Anwendung und Interpretation des Differentials ist, wenn es in seinem "endlichen" Ausdruck verwendet wird:
\[\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \]wo Sie die Variation in y abschätzen möchten, gemessen von \(\Delta y\), aus der Variation in x, gemessen mit \(\Delta x\) und der Ableitung am Punkt.
Manchmal wird dieser \(\Delta y\) genannt Geesamtvariation oder total differential .
Tipps und tricks
Vergessen Sie nicht, dass das Differential als theoretische Definition angenommen werden kann, \(\displaystyle dy = f'(x_0) dx \), was die infinitesimale Variation der y -Ursache durch eine infinitesimale Variation in x angibt.
Es kann auch in seiner Gesamtdifferentialform verwendet werden, in der Sie haben
\[\displaystyle \Delta y \approx f'(x_0)(x-x_0)\]Dies zeigt Ihnen eine angenähte Variation in y, wenn eine Änderung in x (von \(x_0\) zu \(x\)).
Das Zentrum aller algebraischen Taschenrechner beginnt mit der Leistung der Grundzahlen von Brüchen.
Beispiel: differentialrechner
Betrachten Sie die Funktion: \(f(x) = x^2\).Finden Sie sein Differential am Punkt \(x_0 = 1\).
Lösung: Im Fall dieses ersten Beispiels arbeiten wir mit der Funktion \(\displaystyle f(x)=x^2\), für die wir ihr Differential am Punkt \(x_0 = 1\) berechnen müssen.
Die Funktion wurde bereits vereinfacht, sodass wir direkt sein Ableitungsbereich berechnen können:
Differential : Die Formel für das Differential für die Funktion \(\displaystyle f(x)=x^2\) am Punkt \(x_0 = 1\) lautet:
\[dy = f'(x_0)(x - x_0) \]Wir definieren \(\displaystyle y_0 = f(x_0)\), also führt der Wert des Punktes \(x_0 = 1\) in der Funktion zu:
\[y_0 = f(x_0) = f\left(1\right) = 1^2 = 1\]Stecken Sie den Wert des Punktes \(x_0 = 1\) an der berechneten Ableitung führt zu:
\[f'(x_0) = f'\left(1\right) = 2\cdot 1 = 2 \]Dann stecken wir diesen Wert jetzt in die Differentialformel ein, um zu erhalten:
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = 2\left(x-1\right) \]\[\Rightarrow dy = 2x-2 \]Fazit : Daher finden wir, dass das Differential für die Funktion \(\displaystyle f(x)=x^2\) am Punkt \(x_0 = 1\) ist:
\[dy = 2x-2 \]Beispiel: differentialberechnung
Für die angegebene Funktion: \(f(x) = x^3 + 3x^2 - 2\) finden Sie das Differential am Punkt \(x_0 = 2\).
Lösung: Die Funktion, für die wir das Differential finden müssen, ist \(\displaystyle f(x)=x^3+3x^2-2\),
Differentialregung : Wir verwenden die folgende Formel für das Differential, das wir für die angegebene Funktion konstruieren müssen \(\displaystyle f(x)=x^3+3x^2-2\) am angegebenen Punkt \(x_0 = \frac{1}{2}\) lautet:
\[dy = f'(x_0)(x - x_0) \]Beachten Sie, dass \(\displaystyle y_0 = f(x_0)\), was bedeutet, dass wir die Funktion bei \(x_0 = \frac{1}{2}\) bewerten: Wir finden:
\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \left(\frac{1}{2}\right)^3+3\left(\frac{1}{2}\right)^2-2 = -\frac{9}{8}\]Dann erhalten wir das Ableitungsbereich am Punkt \(x_0 = \frac{1}{2}\):
\[f'(x_0) = f'\left(\frac{1}{2}\right) = 3\left(\frac{1}{2}\right)^2+6\cdot \frac{1}{2} = \frac{15}{4} \]Daher bekommen wir Folgendes
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(\frac{15}{4}\right)\left(x-\frac{1}{2}\right) \]\[\Rightarrow dy = \frac{15}{4}x-\frac{15}{8} \]Fazit : Die endgültige Schlussfolgerung ist, dass das Differential, das wir suchen, gegeben wird durch:
\[dy = \frac{15}{4}x-\frac{15}{8} \]Differentialbeispiel
Wir erhalten die Funktion: \(f(x) = \frac{\sin(x)}{x}\).Finden Sie sein Differential am Punkt \(x_0 = \frac{\pi}{2}\).
Lösung:
Die folgende Funktion wurde bereitgestellt: \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), für die wir sein Differential am Punkt \(x_0 = \frac{\pi}{2}\) berechnen müssen.
Die Funktion wurde bereits vereinfacht, sodass wir direkt sein Ableitungsbereich berechnen können:
Berechnung : Jetzt ist es Zeit, das Differential zu finden, das \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\) für den angegebenen Punkt \(x_0 = \frac{\pi}{2}\) zugeordnet ist.Die verwendete Formel lautet:
\[dy = f'(x_0)(x - x_0) \]Wir schließen den Wert des Punktes \(x_0 = \frac{\pi}{2}\) in der berechneten Ableitung, was zu:
\[f'(x_0) = f'\left(\frac{\pi}{2}\right) = \frac{\cos\left(\frac{\pi{}}{2}\right)}{\frac{\pi{}}{2}}-\frac{\sin\left(\frac{\pi{}}{2}\right)}{\left(\frac{\pi{}}{2}\right)^2} = -\frac{4}{\pi{}^2} \]Daher unter Verwendung der Differentialformel:
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(-\frac{4}{\pi{}^2}\right)\left(x-\frac{1}{2}\pi{}\right) \]\[\Rightarrow dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]Fazit : Das entsprechende Differential ist:
\[dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]Andere differenzierungsrechner
Derivat fandden ist ohne Frage ein Schlüsselelement im Kalkül.Derivate geben die Informationen zur Verfügung, um das zu verstehen Änderungsrate von Funktionen.Da haben diese eine intime Verbindung.
Glücklicherweise ist das Finden von Derivaten ein systematischer Prozess (nicht unbedingt einfach), wenn Sie spezifisch folgen Differenzierungsregeln .Die am häufigsten verwendeten Regeln sind die Produktregel Anwesend Quotienteregel und Kettenregel .
Linear oder Annauerungen Erster Ordnung Versuchen Sie konzeptionell, eine Funktion zumindest lokal eine Funktion zu approximieren, und kann Ihnen viel über das Verhalten einer Funktion in der Nähe eines bestimmten Punktes erzählen.






