Mehr zu diesem scheitelpunktrechner

Mit diesem Rechner können Sie eine quadratische Funktion, die Sie angeben, in Scheitelpunktform und zeigt alle Schritte. Sie müssen einen gültigen quadratischen Ausdruck in x angeben. Jede gültige quadratische Funktion ist geeignet.

Zum Beispiel können Sie so etwas wie x^2 + 3x + 4 bereitstellen oder möglicherweise einen Ausdruck bereitstellen, der nicht vereinfacht wird, wie x^2 + 3x - 1/2 x + 3x^2 - 3.

Sobald Sie eine gültige quadratische Funktion angegeben haben, klicken Sie einfach auf "Berechnen", und die Berechnung des Scheitelpunktformulars wird Ihnen angezeigt, wobei alle Schritte von diesem bereitgestellt werden Parabola -Rechner .

Jede quadratische Funktion, die günstig definiert ist, hat eine Scheitelpunktform, aus der es direkt ist, die Koordinaten des Scheitelpunkts zu erhalten, und ob die Parabel "nach oben" oder "nach unten" öffnet.

Wie finde ich die scheitelpunktform für eine parabel?

Alle quadratischen Funktionen werden grafisch durch eine Parabel grafisch dargestellt.Diese Parabel wird je nach Anzeichen des führenden Koeffizienten nach oben oder unten öffnen.

Letztendlich besteht darin, die Parabel in Scheitelpunktform zu bekommen Das Quadratvervollständer .

Was sind die schritte, die die scheitelpunktform berechnen?

So, Wie Funde sie Das Scheitelpunktformular? ?Sie können folgende Schritte befolgen:

• Schritt 1: Identifizieren Sie die quadratische Funktion.Der Ausdruck muss Grad 2 haben, und der führende Koeffizient -Multiplizieren von X² muss sich von Null unterscheiden
• Schritt 2: Wenn der führende Koeffizient mit X² positiv ist, öffnet sich die Parabel nach oben und wenn er negativ ist, öffnet er sich nach unten nach unten
• Schritt 3: Vervollständigen Sie die Quadrate und beachten Sie den Begriff in den Klammern mit x, da er die X-Koordinate des Scheitelpunkts bestimmt
• Schritt 4: Nach Abschluss der Quadrate entspricht die Konstante außerhalb der Klammern (es könnte Null sein) dem Y-Koordinaten des Scheitelpunkts entspricht

Daher können wir sehen, dass der allgemeine Prozess der Scheitelpunktform -Berechnung eng mit dem Prozess des Abschlusses der Quadrate zusammenhängt.

Gibt es eine scheitelpunktformel?

In der Tat, ja, das gibt es. Normalerweise ist die Vervollständigung von Quadraten der lange Weg, den man beschreiten sollte. Angenommen, Sie haben eine Quadratische Funkion , ausgedrückt durch:

\[ f(x) = a x^2 + b x + c\]

Sie haben also bereits eine vereinfachte quadratische Funktion.Die X-Koordinate des Scheitelpunkts wird unter Verwendung der folgenden Formel berechnet:

\[ x_v = \displaystyle \frac{-b}{2a} \]

Ganz einfach, oder? Ja. Aber wie erhält man dann die y-Koordinate des Scheitelpunkts? Man nimmt den Wert \(x_v\) und setzt ihn in die quadratische Funktion ein. Wir erhalten also

\[ y_v = f(x_v) = a x_v^2 + b x_v + c \]

Natürlich kann diese Formel viel schneller sein als ein Prozess des Abschlusses der Quadrate, aber jede Methode hat ihre Verwendung, und die Umstände eines bestimmten Problems werden Ihnen mitteilen, dass Sie verwendet werden..

Quadratische bis vertex -form?

Warum möchten Sie von quadratisch zu Scheitelpunktform gehen?Es gibt viele Gründe: Aus geometrischer Sicht ermöglicht die Scheitelpunktform, die angegebene quadratische Funktion als Übersetzung und Neuauflage einer elementaren Parabel anzuzeigen, wobei die Übersetzung vom Scheitelpunkt bestimmt wird und die Skala mit den führenden Bestimmungen bestimmt wirdKoeffizient.

Die Berechnung mag arbeitsintensiv sein, aber das Parabola -Rechner Wird die Grunzarbeit für Sie erledigen.

Standard zu vertex form?

In der Regel herrscht diesbezüglich ein wenig Verwirrung. Zur Klarstellung: Die Scheitelpunktform ist ein anderer Name für die Standardform. Die Standardform einer quadratischen Funktion \(y = a(x-h)^2 + k\) ist also das Gleiche wie die Scheitelpunktform.

Die Verwirrung rührt daher, dass manchmal die allgemeine Form einer quadratischen Zahl verwendet wird, wenn die Standardform gemeint ist. Die allgemeine Form ist \(y = ax^2 + bx + c\).

Die sinnvolle Frage ist also, wie man von der allgemeinen Form zur Scheitelpunktform kommt, was dasselbe ist wie die Frage, wie man von der allgemeinen Form zur Standardform kommt. Die Antwort ist einfach: Man beginnt mit der allgemeinen Form und geht dann Vervollständer Sie Die Quadrate um zur Standardform zu gelangen.

Beispiel: so finden sie die scheitelpunktform

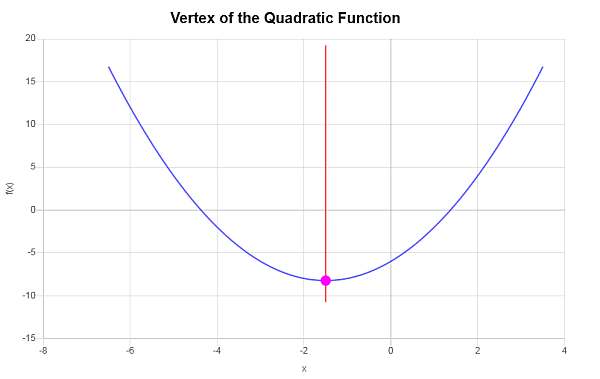
Finden Sie den Scheitelpunkt des folgenden quadratischen Ausdrucks \(f(x) = x^2 + 3x - 6\) mit Hilfe der Scheitelpunktformel

Lösung: Wir müssen die Scheitelpunktform für die quadratische Funktion \(\displaystyle f(x)=x^2+3x-6\) finden.

Zunächst werden die Koordinaten des Scheitelpunkts der Parabel berechnet, die der gegebenen quadratischen Funktion zugeordnet ist.

Für eine quadratische Funktion der Form \(f(x) = a x^2 + bx + c\) wird die x-Koordinate des Scheitelpunkts mit der folgenden Formel berechnet:

\[x_V = \displaystyle -\frac{b}{2a}\]

In diesem Fall ist die Funktion, für die wir den Scheitelpunkt finden müssen, \(f(x) = \displaystyle x^2+3x-6\), was bedeutet, dass die entsprechenden Koeffizienten sind:

\[a = 1\] \[b = 3\] \[c = -6\]

Setzt man die bekannten Werte von \(a\) und \(b\) in die Formel für die x-Koordinate des Scheitelpunkts ein, erhält man:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot 1} = -\frac{3}{2}\]

Nun müssen wir den Wert von \(x_V = \displaystyle -\frac{3}{2}\) in die quadratische Funktion einsetzen, so dass wir erhalten:

\[y_V = f(x_V)\] \[ = 1\cdot \left(-\frac{3}{2}\right)^2+3\cdot \left(-\frac{3}{2}\right)-6=1\cdot\frac{9}{4}+3\cdot \left(-\frac{3}{2}\right)-6=\frac{9}{4}+3\cdot \left(-\frac{3}{2}\right)-6=\frac{9}{4}-\frac{9}{2}-6=-\frac{33}{4}\]

Die x-Koordinate des Scheitelpunkts ist also \(x_V = \displaystyle -\frac{3}{2}\), und die y-Koordinate des Scheitelpunkts ist \(y_V = \displaystyle -\frac{33}{4}\). Dies bedeutet, dass der Punkt, der den Scheitelpunkt darstellt, \( \displaystyle \left(-\frac{3}{2}, -\frac{33}{4}\right)\) ist.

Das Folgende wird grafisch erhalten:

Wir müssen das Quadrat für den quadratischen Ausdruck \(\displaystyle x^2+6x-2\) vervollständigen.

Um das Quadrat zu vervollständigen, müssen folgende Schritte durchgeführt werden:

Schritt 1: In diesem Fall, da die führende Konstante, der Term, der \(x^2\) im gegebenen Polynom multipliziert, \(a = 1\) ist, brauchen wir ihn nicht auszurechnen.

Schritt 2: Wir erzwingen eine '2' vor dem Term \(x\), indem wir feststellen, dass der Term der Ordnung 1 in dem gegebenen quadratischen Ausdruck umgeschrieben werden kann: \(\displaystyle 6 x = 2 \cdot \left(3\right) x\), also erhalten wir \[ x^2+6x-2 = x^2+2 \cdot \left(3\right) x-2 \]

Schritt 3: Der Term, der in diesem Fall mit 2 multipliziert, ist \(\displaystyle 3\). Um die Binomialgleichung zu verwenden, muss das Quadrat \(\displaystyle \left(3\right)^2\) im Ausdruck enthalten sein.

Um das zu erreichen, addieren und subtrahieren wir nun den Term \(\displaystyle \left(3\right)^2 = 9\), um das Quadrat zu vervollständigen. Das Addieren und Subtrahieren desselben Terms ist dasselbe wie das Hinzufügen von Null, es hat also keinen Einfluss auf den Ausdruck: \[ \begin{array}{ccl} \displaystyle x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \end{array}\]

Schritt 4: Wir vervollständigen das Quadrat und vereinfachen die Konstanten: \[ \begin{array}{ccl} x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x+9-2-9 \\\\ \\\\ & = & \displaystyle \left[x^2+2 \cdot \left(3\right) x+\left(3\right)^2\right]-2-9 \\\\ \\\\ & = & \displaystyle \left( x+3 \right)^2-11 \end{array}\]

Schlussfolgerung: Die Funktion in Scheitelpunktform ist also \(\displaystyle f(x) = \left( x+3 \right)^2-11\), womit die Berechnung abgeschlossen ist.

Beispiel: quadratische bis vertexische form

Wandeln Sie die folgende quadratische Form \(f(x) = x^2 + 6x - 2\) in die Scheitelpunktform um. Wie lauten die Koordinaten des Scheitelpunkts? Öffnet sich die Parabel nach oben oder nach unten?

Lösung:

Wir müssen die Scheitelpunktform für die quadratische Funktion \(\displaystyle f(x)=x^2+6x-2\) finden.

Zunächst werden die Koordinaten des Scheitelpunkts der Parabel berechnet, die der gegebenen quadratischen Funktion zugeordnet ist.

Für eine quadratische Funktion der Form \(f(x) = a x^2 + bx + c\) wird die x-Koordinate des Scheitelpunkts mit der folgenden Formel berechnet:

#XYZA

In diesem Fall ist die Funktion, für die wir den Scheitelpunkt finden müssen, \(f(x) = \displaystyle x^2+6x-2\), was bedeutet, dass die entsprechenden Koeffizienten sind:

\[a = 1\] \[b = 6\] \[c = -2\]

Setzt man die bekannten Werte von \(a\) und \(b\) in die Formel für die x-Koordinate des Scheitelpunkts ein, erhält man:

#XYZA

Nun müssen wir den Wert von \(x_V = \displaystyle -3\) in die quadratische Funktion einsetzen, so dass wir erhalten:

\[y_V = f(x_V)\] \[ = 1\cdot \left(-3\right)^2+6\cdot \left(-3\right)-2=1\cdot \left(-3\right)^2+6\cdot \left(-3\right)-2=-3^2+6\cdot \left(-3\right)-2=9-18-2=-11\]

Die x-Koordinate des Scheitelpunkts ist also \(x_V = \displaystyle -3\), und die y-Koordinate des Scheitelpunkts ist \(y_V = \displaystyle -11\). Dies bedeutet, dass der Punkt, der den Scheitelpunkt darstellt, \( \displaystyle \left(-3, -11\right)\) ist.

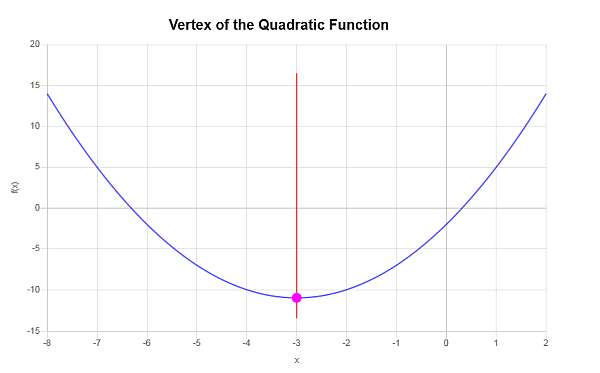
Wir müssen das Quadrat für den quadratischen Ausdruck \(\displaystyle x^2+6x-2\) vervollständigen.

Um das Quadrat zu vervollständigen, müssen folgende Schritte durchgeführt werden:

Schritt 1: In diesem Fall, da die führende Konstante, der Term, der \(x^2\) im gegebenen Polynom multipliziert, \(a = 1\) ist, brauchen wir ihn nicht auszurechnen.

Schritt 2: Wir erzwingen eine '2' vor dem Term \(x\), indem wir feststellen, dass der Term der Ordnung 1 in dem gegebenen quadratischen Ausdruck umgeschrieben werden kann: \(\displaystyle 6 x = 2 \cdot \left(3\right) x\), also erhalten wir \[ x^2+6x-2 = x^2+2 \cdot \left(3\right) x-2 \]

Schritt 3: Der Term, der in diesem Fall mit 2 multipliziert, ist \(\displaystyle 3\). Um die Binomialgleichung zu verwenden, muss das Quadrat \(\displaystyle \left(3\right)^2\) im Ausdruck enthalten sein.

Um das zu erreichen, addieren und subtrahieren wir nun den Term \(\displaystyle \left(3\right)^2 = 9\), um das Quadrat zu vervollständigen. Das Addieren und Subtrahieren desselben Terms ist dasselbe wie das Hinzufügen von Null, es hat also keinen Einfluss auf den Ausdruck: \[ \begin{array}{ccl} \displaystyle x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \end{array}\]

Schritt 4: Wir vervollständigen das Quadrat und vereinfachen die Konstanten: \[ \begin{array}{ccl} x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x+9-2-9 \\\\ \\\\ & = & \displaystyle \left[x^2+2 \cdot \left(3\right) x+\left(3\right)^2\right]-2-9 \\\\ \\\\ & = & \displaystyle \left( x+3 \right)^2-11 \end{array}\]

Schlussfolgerung: Die Funktion in Scheitelpunktform ist also \(\displaystyle f(x) = \left( x+3 \right)^2-11\), womit die Berechnung abgeschlossen ist.

Andere quadratische taschenrechner

Das meiste von Quadratische Taschenrechner auf die eine oder andere Weise auf den Prozess von verlassen Fertigstellung der Quadrate , die es ermöglicht, Dinge innerhalb von Klammern zu gruppieren, die quadratisch sind.

Wie wir in der Scheitelpunktformel sehen können, ist die Scheitelpunktberechnung eng mit dem verknüpft Quadratische Formel und sterben Berechnungswurzeln der Quadratischen Gleisung ..