Über die kettenregel

Mit diesem Rechner können Sie die Kettenregel auf jede von Ihnen bereitgestellte zusammengesetzte Funktion anwenden.A Zusammenesetzte Fungion Entspricht dem Fall, wenn Sie eine Funktion innerhalb einer Funktion bewerten.Damit der Kettenregelrechner funktioniert, müssen Sie eine gültige, differenzierbare zusammengesetzte Funktion bereitstellen.

Ein Beispiel für eine gültige Funktion wäre f (x) = (sin (x))^2, wo wir hier die Funktion 'x^2' haben, die bei einer anderen Funktion bewertet wird, die Sünde (x) ist und a bildetzusammengesetzte Funktion.

Sobald eine gültige, differenzierbare Funktion bereitgestellt wurde, müssen Sie als nächstes auf die Schaltfläche "Berechnen" klicken, wodurch die Berechnungen in Bewegung festgelegt werden und Sie alle Schritte angezeigt werden.

Das Kettenregelderivat ist eine der am häufigsten verwendeten Differenzierungsregel.Dies liegt daran, dass die Funktionszusammensetzung eine der natürlichsten Möglichkeiten ist, neue Funktionen zu konstruieren, die auf elementaren Basis basieren.

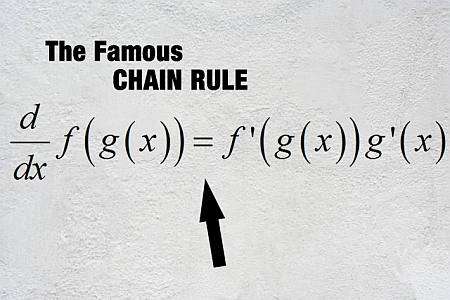
Was ist die kettenregel?

In einfachen Worten ermöglicht die Kettenregel, zusammengesetzte Funktionen zu differenzieren. Dies sind Funktionen, die in anderen Funktionen bewertet werden.Sagen Sie also, wir haben die Funktion \(f(x)\) und \(g(x)\) und wir wissen, wie man die Ableitung dieser Funktionen berechnet, die \(f'(x)\) und \(g'(x)\) sind.

Dann gibt es eine Kettenregellformel Dadurch können wir die Ableitung der zusammengesetzten Funktion \(f \circ g\) berechnen, die als \((f \circ g)(x) = f(g(x))\) definiert ist:

\[\displaystyle (f \circ g)'(x) = f'(g(x))g'(x)\]

Schritte zur verwendung der kettenregel

• Schritt 1: Identifizieren Sie die externe Funktion F (x) und die interne Funktion g (x)
• Schritt 2: Stellen Sie sicher, dass f (x) und g (x) gültige, differenzierbare Funktionen sind, und berechnen Sie die entsprechenden Derivate f '(x) und g' (x).
• Schritt 3: Verwenden Sie die Formel (f \ circ g) '(x) = f' (g (x)) g '(x), die angibt, dass wir die Ableitung der externen Funktion bei der internen Funktion bewerten, und multiplizierender internen Funktion

Beachten Sie, wie die obigen Schritte die Idee der "internen" und "externen" Funktion verwenden.Dies ist möglicherweise kein Standardbegriff, sondern eine Idee, die Ihnen helfen kann, die Rolle jeder Funktion bei der Verwendung der Kettenregel zu identifizieren.

Kettenregel -anwendungen

Die Kettenregel ist in der Tat und ein hervorragendes Werkzeug, um Derivate zu finden, und normalerweise wird der Schlüssel von jedem Derivatnetisch zusammen mit all den anderen Basis Fähigkeitsregeln .Aber die Kettenregel hat eine besondere Interpretation in dem, was genannt wird Verwandte Pregei

Beginnen wir mit einer Form des Schreibens der Kettenregel, dass möglicherweise viele Menschen leichter zu verstehen sind, um einen Kontext zu geben:

\[\displaystyle \frac{dy}{dx} = \displaystyle \frac{dy}{dz} \cdot \frac{dz}{dx} \]

Die obige Form der Kettenregel sagt, dass wenn Sie \(y\) eine Funktion von \(z\) und \(z\) eine Funktion von \(x\) ist, letztendlich \(y\) istEine Funktion von \(x\), und Sie können die Ableitung von \(y\) in Bezug auf \(x\) unter Verwendung der Kettenregel finden.

Wie Sie wahrscheinlich vermutet haben, spielt \(y\) die Rolle von \(f(x)\) (die 'externe' Funktion) und \(z\) spielt die Rolle von \(g(x)\) (die 'interne' Funktion).

Die obige Form der Kettenregel verbindet die Änderungsrate von Y in Bezug auf x mit den Änderungsraten von Y in Bezug auf Z und Z in Bezug auf X und damit den Begriff „verwandte Zinsen“.

Dies ist in der Praxis äußerst nützlich.Beispiel: Der Radius eines Kreises nimmt mit einer Geschwindigkeit von 2 cm/s zu. Wie hoch ist die Änderungsrate des Kreisesbereichs?Sie können also entweder den Radius des Kreises als Funktion von T ausdrücken, was die Tatsache widerspiegelt, dass er mit einer Geschwindigkeit von 2 cm/s ansteigt, oder Sie können die Kettenregel verwenden.

Sie nennen also den Bereich, r den Radius und die Zeit.Was Sie berechnen müssen, ist \(\displaystyle \frac{dA}{dt}\), also verwenden Sie die Kettenregel direkt, da Sie \(A = \pi r^2\) und r '(t) = 2 wissen, also dann

\[\displaystyle \frac{dA}{dt} = \displaystyle \frac{dA}{dr} \cdot \frac{dr}{dt} = 2\pi r \cdot 2 = 4 \pi r \]

Teilendeivatkettenregel

Können Sie die Kettenregel mit verwenden? Telableitungen ?Natürlich ist die teilweise Differenzierung genau wie eine regelmäßige Differenzierung, nur dass die anderen Variablen als konstant angesehen werden, also die üblichen Fähigkeitsregeln anwenden.

Das Ideal der multivariablen Kettenregel gilt also, nur diese eine Variable variiert jeweils.

Kettenregelintegration

Die Kettenregel im Sinne dessen, was sie nicht als Ableitungswerkzeug gilt, sondern wird zu einem unschätzbaren Integrationsinstrument für Substitutionen und Änderungen der Variablen.

Es kann als eine Art umgekehrte Kettenregel konzipiert werden.

Beispiel: verwenden der kettenregel

Berechnen Sie die Ableitung der Funktion: \(f(x) = \sin(\cos(x)) \)

Lösung: Betrachten Sie die Funktion \(\displaystyle f(x)=\sin\left(\cos\left(x\right)\right)\).Diese Funktion entspricht der Zusammensetzung von zwei Funktionen: sin (x) und cos (x), aus denen die Kettenregel in diesem Fall gelten würde.

War ist die Schlussfolgerung : Wir können zu dem Schluss kommen, dass das Derivat, das wir suchen, lautet:

\[f'(x) = -\cos\left(\cos\left(x\right)\right)\sin\left(x\right)\]

und dies schließt die Berechnung ab.

Beispiel für kettenregel

Berechnen Sie die Kettenregel und alle anderen abgeleiteten Regeln: \(\displaystyle \frac{d}{dx} \left( \cos(x^2) \right)^2\)

Lösung: In diesem Beispiel haben wir die Funktion \(\displaystyle f(x)=\cos\left(x^2\right)\), die einer zusammengestellten Funktion entspricht, die angibt, dass die Kettenregel die richtige Ableitung ist (andere Regeln werden entlang der Berechnungen benötigt).

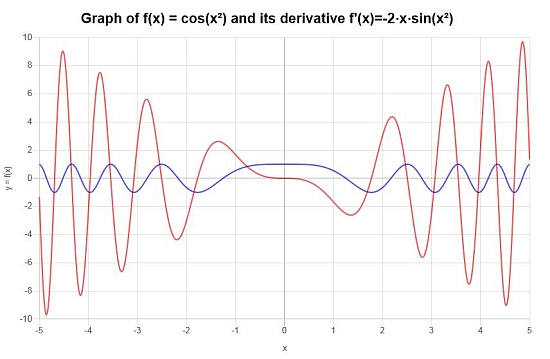
Endgültiger Fähigkeit : Die Schlussfolgerung ist, Dass theLitung der Bereitgestellten Funktion Angegeben Wird Darch:

\[f'(x) = -2x\sin\left(x^2\right)\]

Wirk Können Die Folgende Grafische Darstellung auf Dem -Intervall \([-5, 5]\) ERGNEN:

Beenpiel: eine andere berechnung der kettenregel

Berechnen Sie Die Fähigkeit von \( f(x) = x^2 \sin(x^2)\) Mit der Kettenregel.

Lösung:

Die Folgende Funktion Wurde Bereitgestell: \(\displaystyle f(x)=x^2\sin\left(x^2\right)\), für Die Wir -Sein -Fähigkeit berechnen Müssen.

Die Funktion wurde Bereinfacht, Sodass Wir. Direkt SeinLitungsberich Berechnen Können:

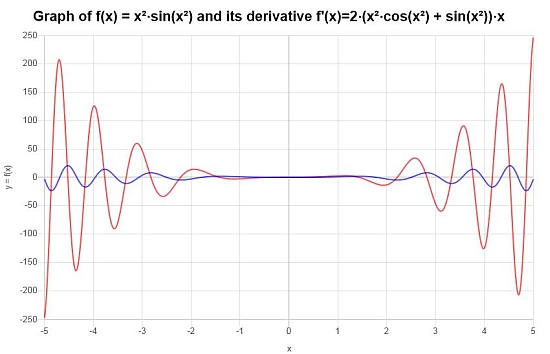
Krieg Das Endgültige Schlussfolgerung : Die Endgültige Schlussfolgerung ist, Dass von uns -Gescheben -Wird -Dard: Dasivat Derivat Derivat.

\[f'(x) = 2\left(x^2\cos\left(x^2\right)+\sin\left(x^2\right)\right)x\]

Grafisch Haven Wir:

Andere derivatrechner

Sicherlich MIT a Derivatnetisch Ermöglichts, die dinge im Umgang mither Koppizierten Funktionen zu Erleichtern.der Prozess der Unterschiede Fähigkeitsregeln , Einschlandlich der Produktregel , Das Quotienteregel und sterben Kettenregel .

Diese Regeln HLFEN Ihenen Dabei, Mit Jeder -Differenzierbaren Funktion Umzughen, Aber der Algebrasche Prozes der Berechnung und Vereinfachung Kann Nicht Unbethedt Einfach Sein.