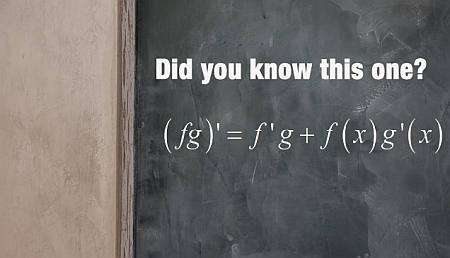Solvers Cálculo

Regla del producto

Instrucciones: Usa esta calculadora para usar la regla del producto, para diferenciar una función dada, mostrando todos los pasos. Escriba la función que desea encontrar la derivada en el cuadro de formulario a continuación.

Más sobre la regla del producto

Esta calculadora te ayudará a encontrar la derivada de funciones usando la regla del producto. Para usar la calculadora, debe proporcionar una función válida para la cual haya un producto involucrado.

Un ejemplo de una función válida podría ser algo como f(x) = x*sin(x), o algo como g(x) = sin(x)*cos(x), solo por mencionar algunas.

Luego, estamos escribiendo la función para la que desea usar la regla del producto, luego debe hacer clic en, todo lo que necesita hacer es hacer clic en el botón "Calcular", y se proporcionarán todos los pasos de los cálculos A usted.

Una de las primeras reglas de derivadas que aprenderá es, de hecho, la regla del producto, ya que la mayoría de las funciones que construye a partir de funciones elementales utilizan el producto de funciones.

Fórmula de la regla del producto

Aprendiendo acerca de regla derivada es quizás lo primero que harás cuando aprendas a encuentra la derivada de una función Y una de las primeras reglas que aprenderás es la regla del producto, sin duda.

La regla del producto, en pocas palabras, es una regla que te ayuda a calcular la derivada de un producto de funciones. La fórmula de la regla del producto es:

\[\displaystyle (f(x) g(x))' = f'(x) g(x) + f(x) g'(x) \]

Pasos para usar la regla del producto

Paso 1: Identifique claramente las funciones f(x) y g(x) que forman el producto con el que está trabajando
Paso 2: Haga simplificaciones si es necesario, manteniendo la estructura del producto
Paso 3: Usa la fórmula de la regla del producto: $(f(x) g(x))' = f'(x) g(x) + f(x) g'(x) $ que consiste en sustituir el valor de las funciones f(x) y g(x), así como de sus derivadas f'(x) y g'(x)

Al trabajar con una derivada de la regla del producto, esencialmente obtiene la derivada del producto en función del conocimiento de las funciones individuales y sus derivadas.

¿qué otras reglas de derivadas existen?

Además de la regla del producto, existen otras reglas importantes, como la regla de la linealidad, la Regla Del Cociente que establece que $\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}$, y el Cadena De Reglas , que establece que $\frac{d}{dx} f(g(x)) = f'(g(x))g'(x)$.

También encontrarás otras reglas mencionadas, como la regla de la potencia, que indica que $\frac{d}{dx} x^n = n x^{n-1}$, para una constante $n$.

Consejos y trucos

La regla del producto se puede considerar como una regla de multiplicación derivada, y la regla del producto juega un papel crucial en Cálculo, por lo que vale la pena aprenderla bien.

Observe que en el caso de funciones multivariables, puede usar la regla de la multiplicación de matrices para operar la regla del producto.

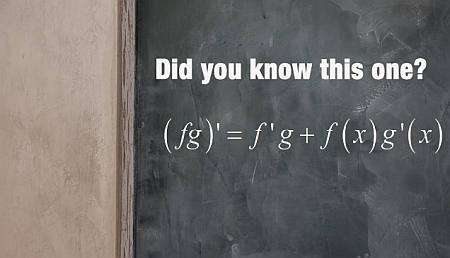
Ejemplo: uso de la regla del producto

Calcular la derivada de: $f(x) = (x-1)(2x+1) $

Solución: Consideramos la siguiente función $\displaystyle f(x)=\left(x-1\right)\left(2x+1\right)$, que necesita ser diferenciada.

$ \displaystyle \frac{d}{dx}\left(\left(2x+1\right)\left(x-1\right)\right)$

By using the Product Rule: $\frac{d}{dx}\left( \left(2x+1\right)\left(x-1\right) \right) = \frac{d}{dx}\left(2x+1\right) \cdot \left(x-1\right)+\left(2x+1 \right) \cdot \frac{d}{dx}\left(x-1\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(2x+1\right) \cdot \left(x-1\right)+\left(2x+1 \right) \cdot \frac{d}{dx}\left(x-1\right)$

By linearity, we know $\frac{d}{dx}\left( x-1 \right) = \frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)$ and $\frac{d}{dx}\left( 2x+1 \right) = \frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)$, so plugging that in:

$ \displaystyle = \,\,$

$\displaystyle \left(\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)\right) \left(x-1\right)+\left(2x+1 \right) \left(\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\right)$

Since the derivative of a constant is 0, we find that:

$ \displaystyle = \,\,$

$\displaystyle \left(\frac{d}{dx}\left(2x\right)\right) \left(x-1\right)+\left(2x+1 \right) \left(\frac{d}{dx}\left(x\right)\right)$

It is known that $\frac{d}{dx}\left(x\right) = 1$

$ \displaystyle = \,\,$

$\displaystyle \left(\frac{d}{dx}\left(2x\right)\right) \left(x-1\right)+\left(2x+1 \right)$

So, we directly get: $\frac{d}{dx}\left( 2x \right) = 2$

$ \displaystyle = \,\,$

$\displaystyle \left(2\right) \left(x-1\right)+\left(2x+1 \right)$

and then we find

$ \displaystyle = \,\,$

$\displaystyle 2x+1+2\left(x-1\right)$

Note that $(2) \cdot (x-1) = 2x-2\cdot 1 = 2x-2$, due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

$ \displaystyle = \,\,$

$\displaystyle 2x+1+2x-2$

Grouping the terms with $x$

$ \displaystyle = \,\,$

$\displaystyle \left(2+2\right)x+1-2$

Grouping together numerical values and operating the terms that were grouped with $x$

$ \displaystyle = \,\,$

$\displaystyle 4x+1-2$

Reducing the integers that can be subtracted together: $\displaystyle 1-2 = -1$

$ \displaystyle = \,\,$

$\displaystyle 4x-1$

Conclusión : Por lo tanto, se concluye que la derivada de la función es:

\[f'(x) = 4x-1\]

Gráficamente, el siguiente diagrama representa la situación:

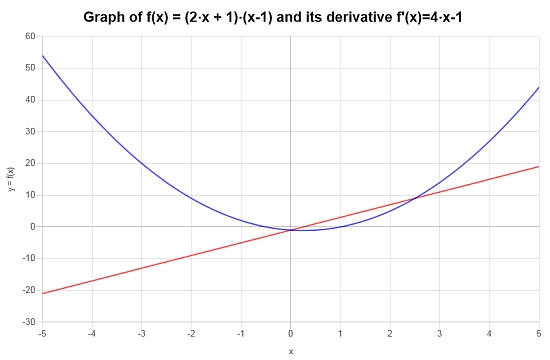
Ejemplos de reglas de productos

Encuentra la derivada de: $f(x) = x \sin(x)$

Solución: En este ejemplo, la función dada es $\displaystyle f(x)=x\sin\left(x\right)$. Encontremos su derivada

$ \displaystyle \frac{d}{dx}\left(x\sin\left(x\right)\right)$

Usamos la regla del producto: $\frac{d}{dx}\left( x\sin\left(x\right) \right) = \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)$

Derivando directamente encontramos: $\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \cos\left(x\right)$

Entonces después de simplificar obtenemos que:

$ \displaystyle = \,\,$

$\displaystyle x\cos\left(x\right)+\sin\left(x\right)$

Conclusión : Por lo tanto, encontramos que la derivada viene dada por la siguiente fórmula:

\[f'(x) = x\cos\left(x\right)+\sin\left(x\right)\]

El siguiente gráfico se construye para la función y su derivada:

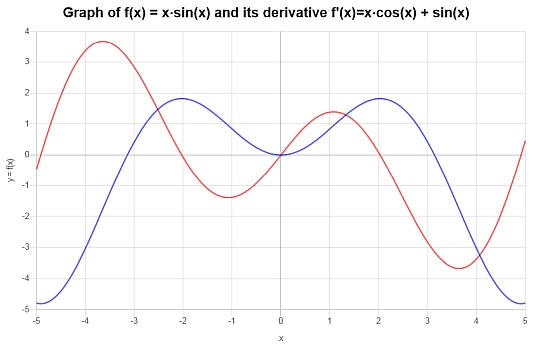
Ejemplo: otro cálculo de regla de producto

Diferencie la siguiente función $ f(x) = x (x+1)^2 $.

Solución: Finalmente, para este ejemplo la función dada es $\displaystyle f(x)=x\left(x+1\right)^2$. Como hay un producto de función, podemos usar la regla del producto para diferenciar.

$ \displaystyle \frac{d}{dx}\left(\left(x+1\right)^2x\right)$

Usamos la regla del producto: $\frac{d}{dx}\left( \left(x+1\right)^2x \right) = \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 \cdot \frac{d}{dx}\left(x\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 \cdot \frac{d}{dx}\left(x\right)$

Sabemos que $\frac{d}{dx}\left(x\right) = 1$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 $

Usando la regla de la potencia para un exponente constante: $\frac{d}{dx}\left( \left(x+1\right)^2 \right) = 2x+1\cdot \frac{d}{dx}\left(x+1\right)$

$ \displaystyle = \,\,$

$\displaystyle \left(2x+1\cdot \frac{d}{dx}\left(x+1\right)\right) x+\left(x+1\right)^2 $

Por linealidad, conocemos $\frac{d}{dx}\left( x+1 \right) = \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)$, así que conectando eso:

$ \displaystyle = \,\,$

$\displaystyle \left(2x+1\left(\frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)\right)\right) x+\left(x+1\right)^2 $

La derivada de una constante es 0, entonces:

$ \displaystyle = \,\,$

$\displaystyle \left(2x+1\left(\frac{d}{dx}\left(x\right)\right)\right) x+\left(x+1\right)^2 $

Sabemos que $\frac{d}{dx}\left(x\right) = 1$

$ \displaystyle = \,\,$

$\displaystyle \left(2x+1\right) x+\left(x+1\right)^2 $

que luego conduce a

$ \displaystyle = \,\,$

$\displaystyle \left(x+1\right)^2+2\left(x+1\right)x$

Ampliando los términos: $\left(x+1\right)^2 = \left(x+1\right)\left(x+1\right)$

$ \displaystyle = \,\,$

$\displaystyle \left(x+1\right)\left(x+1\right)+2\left(x+1\right)x$

Observa que $(x+1) \cdot (x+1) = x^2+1x+1x+1^2 = x^2+2x+1$, como podemos usar la propiedad distributiva en cada término de la expresión de la izquierda, con respecto a los términos de la derecha

$ \displaystyle = \,\,$

$\displaystyle x^2+2x+1+2\left(x+1\right)x$

Tenga en cuenta que $(x+1) \cdot (x) = x^2+1x = x^2+x$, debido a que podemos usar la propiedad distributiva en cada término de la expresión de la izquierda, con respecto a los términos de la derecha

$ \displaystyle = \,\,$

$\displaystyle x^2+2x+1+2\left(x^2+x\right)$

Obtenemos $(2) \cdot (x^2+x) = 2x^2+2x = 2x^2+2x$, usando la propiedad distributiva en cada término de la expresión de la izquierda, con respecto a los términos de la derecha

$ \displaystyle = \,\,$

$\displaystyle x^2+2x+1+2x^2+2x$

Agrupando los términos con $x$, $x^2$

$ \displaystyle = \,\,$

$\displaystyle \left(2+2\right)x+\left(1+2\right)x^2+1$

Juntando los números enteros y simplificando los términos que se agruparon con $x$, $x^2$

$ \displaystyle = \,\,$

$\displaystyle 4x+3x^2+1$

Entonces obtenemos

$ \displaystyle = \,\,$

$\displaystyle \left(3x+1\right)\left(x+1\right)$

Conclusión : En base a lo calculado anteriormente, se encuentra que la derivada correspondiente es:

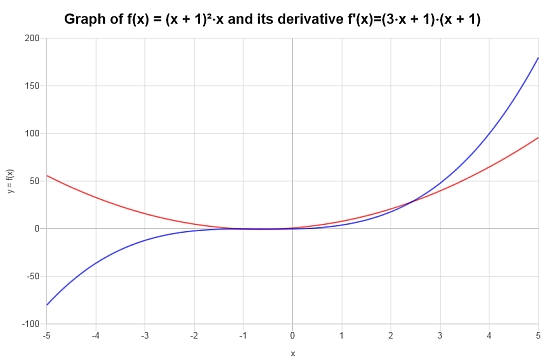
\[f'(x) = \left(3x+1\right)\left(x+1\right)\]

El siguiente gráfico se obtiene para la función dada en el intervalo $[-5, 5]$:

Más calculadoras de derivadas

Pocas personas estarán en desacuerdo con esa diferenciación junto con la integración y el punto central del Cálculo. Calcular una derivada es una habilidad crucial que necesitará aprender como estudiante de cálculo.

Puedes aprender diferentes 'sabores' de diferenciación, incluyendo diferenciación parcial tanto como diferenciación implícita , que se utilizan en diferentes contextos de aplicación.

Las aplicaciones incluyen Linea tangente cálculo, que es lo mismo que un Aproximación Lineal , así como el uso de derivadas de orden superior, comenzando con derivadas de segundo orden .