Calculadoras Cálculo

Calculadora de línea tangente

Instrucciones: Utilice esta calculadora para calcular la recta tangente de una función dada, en un punto dado, mostrando todos los pasos. Escriba la función y el punto correspondiente en el cuadro de formulario a continuación.

Acerca de esta calculadora de recta tangente

Esta calculadora te permitirá realizar sin problemas los cálculos necesarios para obtener la recta tangente de una función, en un punto dado, mostrando todos los pasos.

Todo lo que necesita hacer es proporcionar una función válida f(x) y un punto en el que desea la línea tangente. La función podría ser cualquier función diferenciable válida como f(x) = sin(x), o f(x) = x^2 - x + 1, etc. El punto puede ser cualquier expresión numérica válida, como 1/2 para ejemplo.

Luego, cuando se haya proporcionado la información requerida y sea válida, debe hacer clic en "Calcular" para que se le muestren todos los pasos de la ecuación de la línea tangente.

Las aplicaciones de la recta tangente abundan en la ciencia por todas partes. También llamado primer orden o aproximación lineal , tiene un significado muy profundo en Física e Ingeniería, donde la idea de la principal contribución al cambio (la parte de primer orden) es aquella que revela mucha información sobre un proceso.

¿qué es la recta tangente?

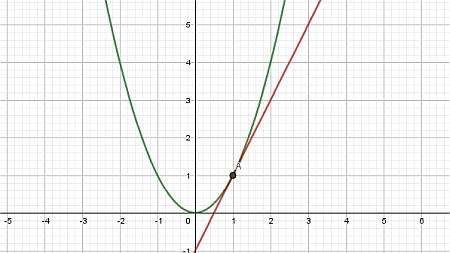
En términos simples, una línea tangente es una línea que intersecta una curva, pero la intersecta en un solo punto (al menos localmente). Esta línea tangente se construye fijando un punto $x_0$ y luego tomando un punto diferente $x_1$.

Entonces, al construir la recta que pasa por los puntos $(x_0, f(x_0))$ y $(x_1, f(x_1))$, obtenemos lo que se llama Linea secante , como se muestra en el siguiente gráfico:

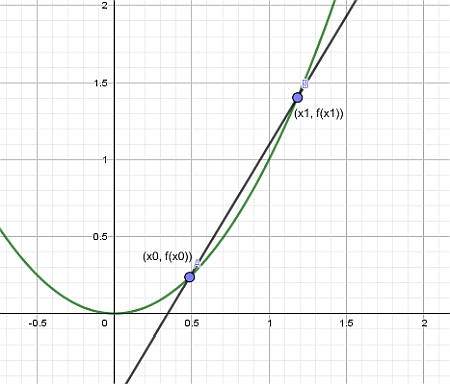
Finalmente, dejamos que el punto $x_1$ se aproxime a $x_0$, y lo que obtenemos es la recta tangente:

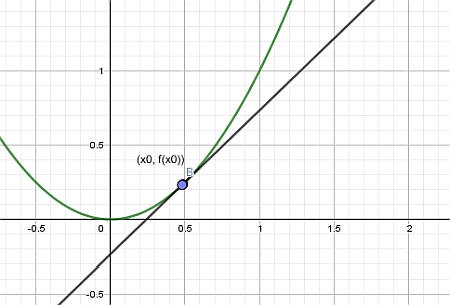
Pasos para encontrar la recta tangente geométricamente

Paso 1: Identifica la función f(x) con la que quieres trabajar y el punto x0. Necesitas a los dos
Paso 2: El punto (x0, f(x0)) estará sobre la curva de la función f(x). plotearlo
Paso 3: Elija un punto (x1, f(x1)), para un x1 que sea diferente de x0 (puede estar a la izquierda oa la derecha de x). plotearlo
Etapa 4: Dibuja una recta que pase por los puntos (x0, f(x0)) y (x1, f(x1))
Paso 5: Elija un punto x2 que esté a medio camino entre x0 y x1, y dibuje una línea que pase por los puntos (x0, f(x0)) y (x2, f(x2))
Paso 6: Repita este proceso varias veces

Este método gráfico te ayudará a tener una idea aproximada de cómo se ve la línea tangente, pero es una aproximación (a menos que la función f(x) sea lineal).

Fórmula de la recta tangente

El método de aproximación usando rectas secantes puede darte una idea de lo que estás buscando, pero afortunadamente existe una fórmula exacta para calcular la recta tangente a una función en un punto $x_0$. La fórmula de la recta tangente es:

\[\displaystyle y = f(x_0) + f'(x_0) (x - x_0) \]

Sencillo, ¿eh? En términos simples, esta fórmula dice que la línea tangente es una recta que pasa por el punto $(x_0, f(x_0))$ y que tiene una pendiente de $m = f'(x_0)$

Entonces, en términos sencillos, la pendiente de la recta tangente en un punto dado es exactamente la derivada de la función en ese punto.

Pasos para aplicar la fórmula de la recta tangente

Paso 1: Identifica la función f(x) y el punto x0
Paso 2: Calcule el valor de la función en x0, que es f(x0)
Paso 3: Calcule la derivada de f(x) en el punto x0, por lo que necesita f'(x0)
Etapa 4: Aplicar directamente la fórmula de la recta tangente $y = f(x_0) + f'(x_0) (x - x_0)$

Una vez que tengas la ecuación de la línea , puede transformarlo al formato que sea más útil para la situación actual.

La pendiente de la recta tangente

Una de las conclusiones clave es que la pendiente de la recta tangente en $x_0$ es exactamente $f'(x_0)$, que es la derivada en el punto $x_0$. Esto proporciona una interpretación clara y extremadamente útil de la derivada en términos geométricos.

Esta conexión permite encontrar la ecuación de la recta tangente a una curva dada en un punto dado simplemente mirando la derivada de la función.

¿cuándo tienes una recta tangente horizontal?

Una recta tangente horizontal ocurrirá cuando el punto elegido $x_0$ cuando la derivada correspondiente en ese punto sea igual a cero. En ese caso, la línea tangente (que es la línea que toca la curva en un punto localmente) será paralela al eje y.

Entonces, todo lo que necesitas saber para identificar rectas tangentes horizontales es encontrar puntos donde la derivada de la función sea cero.

¿cuándo tienes una recta tangente vertical?

Una recta tangente vertical ocurrirá cuando la derivada sea "infinita" en un punto. Esta es una forma sencilla de decir que es donde la derivada no está definida en un punto dado, pero converge a infinito a medida que nos acercamos al punto.

Por ejemplo, se podría decir que $f(x) = \frac{1}{x}$ tiene una recta tangente vertical en x = 0. Sin embargo, se podría argumentar que no hay recta tangente porque la derivada no está bien definida en x = 0.

Ejemplo: recta tangente

Encuentra la ecuación de la recta tangente para $f(x) = x^2 - 2x + 1$, en el punto $x_0 = 2$.

Solución: La siguiente función es con la que necesitamos trabajar: $\displaystyle f(x)=x^2-2x+1$. Primero, necesitamos calcular su derivada.

La función ya vino simplificada, por lo que podemos proceder directamente a calcular su derivada:

$ \displaystyle \frac{d}{dx}\left(x^2-2x+1\right)$

By linearity, we know $\frac{d}{dx}\left( x^2-2x+1 \right) = \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)$, so plugging that in:

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)$

Since the derivative of a constant is 0, we find that:

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)$

Directly we get: $\frac{d}{dx}\left( 2x \right) = 2$ and using the Power Rule for polynomial terms: $\frac{d}{dx}\left( x^2 \right) = 2x$

$ \displaystyle = \,\,$

$\displaystyle 2x-2$

Linea Tangente : La ecuación de la recta tangente de la función $\displaystyle f(x)=x^2-2x+1$ en el punto $x_0 = 2$ es:

\[y = y_0 + f'(x_0)(x - x_0) \]

En este caso, $\displaystyle y_0 = f(x_0)$, entonces reemplazando el valor del punto $x_0 = 2$ en la función conduce a:

\[y_0 = f(x_0) = f(2) = 2^2-2\cdot 2+1 = 1 \]

Además, reemplazar el valor del punto $x_0 = 2$ en la derivada calculada conduce a:

\[f'(x_0) = f'(2) = 2\cdot 2-2 = 2 \]

Entonces, ahora reemplazamos estos valores en la fórmula de la línea tangente para obtener:

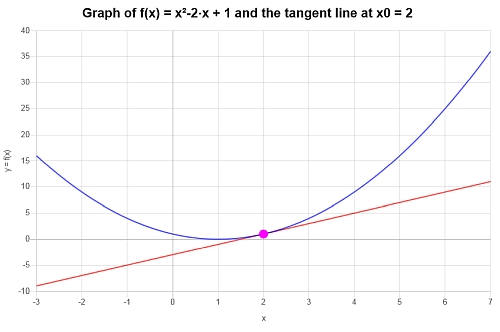
\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 1+2\left(x-2\right) = 2x-3 \]

Conclusión : Por lo tanto, se encuentra que la recta tangente de la función $\displaystyle f(x)=x^2-2x+1$ en el punto $x_0 = 2$ es:

\[y = 2x-3 \]

Se obtiene el siguiente gráfico para la función dada y su recta tangente en $x_0 = 2$:

Ejemplo: ecuación de recta tangente

¿Cuál es la recta tangente en x = 1/2, para la función $f(x) = \sin(x) + 1$?

Solución:

Se ha proporcionado la siguiente función: $\displaystyle f(x)=\sin\left(x\right)+1$, para la cual necesitamos calcular su derivada.

La función ya vino simplificada, por lo que podemos proceder directamente a calcular su derivada:

$ \displaystyle \frac{d}{dx}\left(\sin\left(x\right)+1\right)$

By linearity, we know $\frac{d}{dx}\left( \sin(x)+1 \right) = \frac{d}{dx}\left(\sin(x)\right)+\frac{d}{dx}\left(1\right)$, so plugging that in:

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(\sin\left(x\right)\right)+\frac{d}{dx}\left(1\right)$

The derivative of a constant is 0, so then:

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(\sin\left(x\right)\right)$

Directly differentiating: $\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)$

$ \displaystyle = \,\,$

$\displaystyle \cos\left(x\right)$

Linea Tangente : Encontramos que la ecuación correspondiente de la recta tangente en el punto $x_0 = \frac{1}{2}$ está dada por:

\[y = y_0 + f'(x_0)(x - x_0) \]

Pero en este caso específico, $\displaystyle y_0 = f(x_0)$, lo que significa que necesitamos reemplazar el valor del punto $x_0 = \frac{1}{2}$ en la función, por lo que obtenemos:

\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \sin\left(\frac{1}{2}\right)+1\]

Ahora, haciendo lo mismo en la derivada, para $x_0 = \frac{1}{2}$ encontramos

\[f'(x_0) = f'\left(\frac{1}{2}\right) = \cos\left(\frac{1}{2}\right) \]

Ahora solo tenemos que conectar los valores, por lo que encontramos que

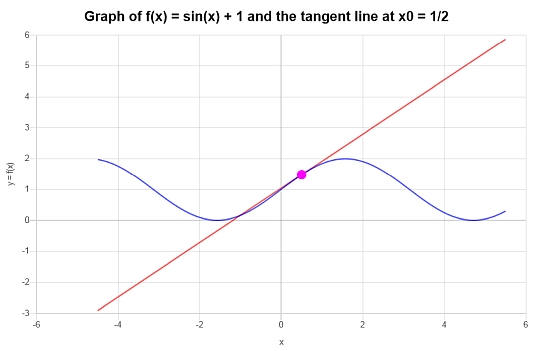
\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = \sin\left(\frac{1}{2}\right)+1+\cos\left(\frac{1}{2}\right)\left(x-\frac{1}{2}\right) = x\cos\left(\frac{1}{2}\right)-\frac{1}{2}\cos\left(\frac{1}{2}\right)+\sin\left(\frac{1}{2}\right)+1 \]

Conclusión : Encontramos que la recta tangente correspondiente que estamos buscando, en el punto correspondiente $x_0 = \frac{1}{2}$ está dada por

\[y = x\cos\left(\frac{1}{2}\right)-\frac{1}{2}\cos\left(\frac{1}{2}\right)+\sin\left(\frac{1}{2}\right)+1 \]

Gráficamente:

Ejemplo: otra recta tangente

¿Cuál es la recta tangente en x = 0, para la función $f(x) = \cos(x)$? ¿Tiene sentido este resultado?

Solución: Observe que $f'(x) = -\sin(x)$, luego $f'(0) = -\sin(0) = 0$. Esto es, la recta tangente tiene una pendiente de m = 0 en x = 0, entonces la ecuación de la recta tangente es simplemente $y = y_0 = \cos(0) = 1$. Esto tiene sentido porque en este caso, la línea tangente es una línea horizontal.

Más calculadoras de diferenciación

Algunas personas pueden afirmar que la diferenciación es un ejercicio relativamente sencillo y que usar un calculadora de derivadas puede que no sea necesario, pero en verdad, el cálculo de las derivadas aún puede ser bastante engorroso y puede requerir mucho tiempo. cálculos algebraicos .

Cuando tienes una expresión con más de una variable, para encontrar la derivada necesitarás determinar si las variables son independientes entre sí, en cuyo caso usas Derivadas parciales , o si hay una ecuación que vincule las variables, en cuyo caso necesitaría usar diferenciación implícita .

Las dos áreas principales del cálculo diferencial son la integración y la diferenciación, y ambas tienen amplias aplicaciones en todas partes. Derivadas parciales aparecen con gran extensión en las aplicaciones de ingeniería y economía.

Por un lado, la diferenciación trata con tasas infinitesimales de cambio, mientras que la integración trata con la suma de tasas infinitesimales de cambio y, admirablemente, están estrechamente vinculadas por la Teorema fundamental del cálculo .