Diferenciación implícita

Esta calculadora lo ayudará a realizar la derivación implícita de una ecuación que involucra las variables x e y. Debe proporcionar una ecuación válida como x ^ 2 + y ^ 2 = 1, o xy - x ^ 2 y ^ 2 = 0, etc.

Una vez que proporciones una ecuación válida que involucre dos variables (\(x\) y \(y\)), todo lo que tienes que hacer es hacer clic en el botón "Calcular" y se mostrarán todos los pasos de la diferenciación implícita correspondiente.

Esto es un calculadora dy/dx con pasos en el sentido de que te mostrará todos los pasos relevantes del cálculo de la derivada de una variable con respecto a otra, siempre y cuando esas dos variables estén relacionadas en una ecuación. Esta relación es la que permite encontrar la correspondiente derivada implícita .

Tener una ecuación que relacione las dos variables \(x\) y \(y\) nos dice que deberíamos poder expresar \(y\) como una función de \(x\) y escribir \(y = y(x)\). A menudo, no podemos expresar explícitamente \(y\) como una función de \(x\); asumimos que existe dicha función, en cuyo caso, tiene sentido diferenciar \(y\) con respecto a \(x\).

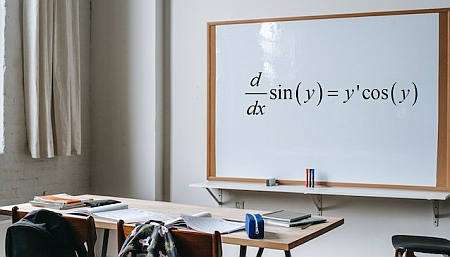
¿qué es la diferenciación implícita?

La diferenciación implícita es una cálculo de diferenciación técnica basada en el supuesto de que es posible establecer a partir de una ecuación dada que involucra \(x\) y \(y\) que \(y\) es una función de \(x\) aunque muchas veces no podemos escribir explícitamente dicha función.

Una vez que se hace esa suposición, asumimos que podemos calcular \(\frac{dy}{dx}\) y podemos usar todos los métodos conocidos. Reglas Derivadas ( Regla Del Producto , Regla Del Cociente y Cadena De Reglas ) para diferenciar ambos lados de la ecuación y resolver para \(\frac{dy}{dx}\).

¿qué es el método de diferenciación implícita?

El método de diferenciación implícita es un método que le permite calcular una derivada de expresiones que no están directamente puestas en formato \(f(x)\). Es decir, cuando se nos da una función de una variable \(x\), por ejemplo, simplemente seguimos adelante y diferenciamos esa función.

Pero cuando dos variables \(x\) y \(y\) están relacionadas mediante una ecuación, como \(x^2+y^2 = 1\) por ejemplo, también puedes diferenciar y con respecto a x, bajo el método tradicional, necesitarás RESOLVER y en términos de x, y ENTONCES podrás diferenciar.

Usando la diferenciación implícita, puedes diferenciar directamente, simplemente asumiendo que \(y = y(x\), y haciendo uso de la Cadena De Reglas .

Pasos para usar la diferenciación implícita

• Paso 1: Identifica la ecuación que involucra dos variables x e y. Simplifica cualquier término redundante
• Paso 2: Suponga que y es una función de x, y = y(x), por lo que tiene sentido calcular la derivada de y con respecto a x
• Paso 3: Calcular la derivada de ambos lados de la ecuación usando todos los Reglas Derivadas necesitas. Esto conducirá a una igualdad en la que x, y e y' están presentes potencialmente
• Etapa 4: Resuelve lo que obtuviste en el Paso 3 para y'. Tenga en cuenta que y' generalmente se escribirá como una función de x e y, lo cual está bien, ya que y también depende de x

Esta es una metodología muy general, y tendrá sutilezas de un caso a otro, pero ese es el modelo que debería funcionar en la mayoría de los casos, con la dificultad adicional de manipulaciones algebraicas potenciales.

Por qué usar una calculadora de diferenciación implícita

La diferenciación implícita puede ser confusa a veces, si no tiene muy claro qué está diferenciando y con respecto a qué variable. Una calculadora lo ayudará a comparar su resultado y una característica especial de nuestra calculadora es que se muestran todos los pasos del proceso.

Esa es una ayuda crucial para usted, porque le mostrará exactamente qué regla derivada y dónde la aplicó.

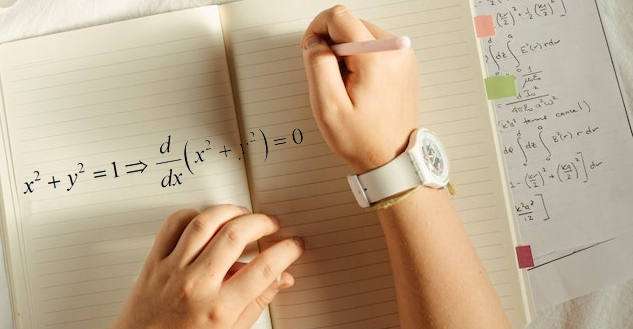
¿cuál es el sentido de la diferenciación implícita?

Esa es una pregunta razonable. Si tiene una ecuación que involucra x e y, ¿por qué no resolver y en términos de x y usar el cálculo de derivadas regulares para obtener la derivada de y con respecto a x? Te puedo dar al menos dos buenas razones:

• Razón 1: Puede darse el caso de que NO PUEDAS resolver y en términos de x explícitamente. Puede haber una función, pero no puede simplemente encontrarla. Piensa en y + tan(y) = x^2
• Razón 2: Incluso si te sucede resolver y en términos de x , puede ser una expresión realmente complicada, y el cálculo de la derivada podría ser muy enrevesado y difícil. Por lo general, la diferenciación implícita es algebraicamente simple, en términos relativos

¿la derivada implícita depende de y?

No siempre, pero sí a menudo. Ahora, esto solo dice que \(\frac{dy}{dx}\) puede depender de x e y, pero como y depende de x, solo dice que, como se esperaba, \(\frac{dy}{dx}\) depende de x.

En la siguiente sección se presentarán diferentes ejemplos de diferenciación implícita.

Segunda derivada implícita

Una pregunta es: ¿se puede calcular la segunda derivada mediante diferenciación implícita? La respuesta es sí. Simplemente haces lo mismo que con la primera derivada usando diferenciación implícita, simplemente asumes que \(y\) es una función de \(x\), entonces escribes \(y = y(x)\) y puedes derivar todo lo que desees.

Por ejemplo, digamos que desea encontrar \(\frac{d^2y}{dx^2}\) dada la ecuación \(x^2+y^2=1\). Diferenciando ambos lados con respecto a \(x\):

\[ \frac{d}{dx}\left(x^2+y^2\right)=\frac{d}{dx}\left(1\right)\] \[ \Rightarrow 2x+2yy' = 0\]

Ahora, derivas nuevamente con respecto a x:

\[ \frac{d}{dx}\left(2x+2yy'\right)=\frac{d}{dx}\left(0\right)\] \[ \Rightarrow 2+2(y')^2+2yy'' = 0\]

y ahora resolvemos para \(y''\):

\[ \Rightarrow y'' = -\frac{(2+2(y')^2)}{2y}\] \[ \Rightarrow y'' = -\frac{(1+(y')^2)}{y}\]

Ejemplo: ejemplo de diferenciación implícita

Encuentre \(\frac{dy}{dx}\) para la ecuación: \(x^2 - y^2 = 2y\)

Solución: Este es un ejemplo de diferenciación implícita. Se ha proporcionado la siguiente ecuación: \(\displaystyle x^2-y^2=2y\), para la cual necesitamos realizar una diferenciación implícita, donde asumimos que \(y\) es una función de \(x\).

La ecuación no necesita más simplificación, por lo que podemos proceder con la diferenciación implícita:

Necesitamos derivar ambos lados de la ecuación con respecto a \(x\), y en ambos lados asumimos que \(y = y(x)\).

Lado izquierdo : Diferenciando el lado izquierdo con respecto a \(x\)

Lado derecho : Diferenciando el lado derecho con respecto a \(x\)

Por lo tanto, después de diferenciar ambos lados con respecto a \(x\) se obtiene lo siguiente:

\[\displaystyle 2x-2y\frac{dy}{dx} = 2\frac{dy}{dx}\]

Poniendo todos los términos de un lado:

\[-2\,y\frac{d}{dx}y+2\,x-2\,\frac{d}{dx}y = 0\]

Agrupando todo lo que contiene \(\displaystyle \frac{dy}{dx}\):

\[-2\,{\left(y+1\right)}\frac{d}{dx}y+2\,x = 0\]

Finalmente, resolviendo para \(\displaystyle \frac{dy}{dx}\), se obtiene:

\[\displaystyle \frac{dy}{dx} = \frac{x}{y+1}\]

Ejemplo: más cálculos de diferenciación implícita

¿Cuál es la pendiente de la recta tangente a un círculo unitario en el punto \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\)?

Solución: Observe que la ecuación del círculo unitario es \(\displaystyle x^2 + y^2 = 1\), que define implícitamente \(y\) como una función de \(x\). Para encontrar la recta tangente, necesitamos calcular \(\frac{dy}{dx}\) en el punto especificado. Usando diferenciación implícita, diferenciamos ambos lados de la ecuación que define el círculo unitario: \[\displaystyle x^2 + y^2 = 1\] \[\Rightarrow \displaystyle \frac{d}{dx}\left(x^2 + y^2\right) = \frac{d}{dx}\left(1\right)\] \[\Rightarrow \displaystyle 2x+2yy' = 0 \] \[\Rightarrow \displaystyle 2yy' = -2x \] \[\Rightarrow \displaystyle y' = -\frac{x}{y} \]

El punto de interés es \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\), entonces.

\[\displaystyle y' \left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right) = -\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = -1\]

Esto implica que la pendiente de la recta tangente en el punto \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\) es \(m = -1\), lo que implica que la ecuación de la recta tangente en ese punto es

\[\displaystyle y - \frac{\sqrt{2}}{2} = -\left(x-\frac{\sqrt{2}}{2}\right)\] \[\Rightarrow \displaystyle y = \frac{\sqrt{2}}{2} - x + \frac{\sqrt{2}}{2}\] \[\Rightarrow \displaystyle y = \sqrt{2} - x \]

Ejemplo de diferenciación implícita

Considere la ecuación: \( \displaystyle \frac{2}{3} x + y^2 = \frac{2}{5} \). Calcular \(\frac{dy}{dx}\)

Solución: En este caso tenemos la siguiente ecuación: \(\displaystyle \frac{2}{3} x + y^2 = \frac{2}{5}\), por lo que necesitamos hacer una diferenciación implícita, bajo el supuesto de que \(y\) depende de\(x\).

No se requiere una mayor simplificación de la ecuación, por lo que nos permite proceder con la diferenciación implícita:

Ahora necesitamos calcular la derivada de ambos lados con respecto a la variable \(x\), suponiendo que \(y = y(x)\).

Lado izquierdo : Diferenciando el lado izquierdo con respecto a la variable \(x\)

Lado derecho : Ahora diferenciamos el lado derecho con respecto a \(x\)

Por tanto, el resultado que se obtiene tras diferenciar ambos lados con respecto a \(x\) es:

\[\displaystyle \frac{2}{3}+2y\frac{dy}{dx} = 0\]

Por lo tanto, ahora podemos resolver \(\displaystyle \frac{dy}{dx}\) para obtener:

\[\displaystyle \frac{dy}{dx} = -\frac{1}{3\,y}\]

Calculadoras de cálculo más útiles

Una de las aplicaciones más interesantes de la reglas de las derivadas es el concepto de diferenciación implícita. Tiene aplicaciones en Física, Economía e Ingeniería, y es extremadamente práctico para describir la tasa de cambio a lo largo de las curvas.

Un tipo diferente de derivados son Derivadas parciales en el cual, a diferencia del caso de diferenciación implícita donde asumimos que y = y(x), en ese caso y se considera una constante cuando x cambia.