Solvers Cálculo

Reglas derivadas

Instrucciones: Usa esta calculadora de derivadas para encontrar la derivada de cualquier función que proporciones, usando las reglas de derivadas más comunes, mostrando todos los pasos. Escriba la función a la que desea aplicar reglas derivadas en el cuadro de formulario a continuación.

Acerca de las reglas derivadas

Esta calculadora le permitirá calcular la derivada de una función que proporcione al aplicar las reglas básicas de diferenciación requeridas, mostrando todos los pasos del proceso y anotando dónde se aplica cada regla.

Solo necesita proporcionar una función válida que sea diferenciable (lo que significa que tiene una derivada). Por ejemplo, una función válida podría ser f(x) = 1/3*x*sin(x), solo por mencionar un ejemplo.

Luego, cuando ya haya escrito su función, simplemente haga clic en "Calcular" para obtener todos los pasos de la diferenciación que se muestran.

La simplicidad de las reglas de las derivadas hace que el proceso de diferenciación sea reconocido como 'fácil', un juicio que quizás sea una exageración.

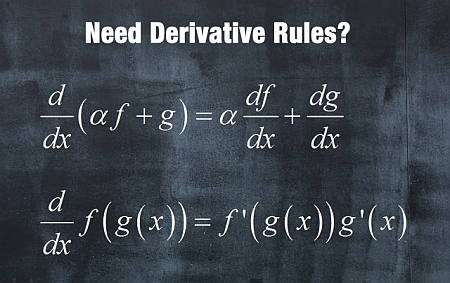
Reglas básicas de derivadas

Hay cuatro reglas básicas de derivadas para que las aprendas

Regla De Linealidad: Para funciones $f(x)$ y $g(x)$, y una constante $a$, entonces la derivada es una operación lineal: $(af(x)+g(x))' = af'(x)+g'(x)$
Regla Del Producto Para las funciones $f(x)$ y $g(x)$, la derivada del producto es $(f(x)g(x))' = f'(x)g(x) + f(x)g'(x)$
Regla Del Cociente: Para las funciones $f(x)$ y $g(x)$, la derivada del cociente es $\left(\frac{f(x)}{g(x)}\right)' = \left(\frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)}\right)$
Cadena De Reglas Para las funciones $f(x)$ y $g(x)$, la derivada de la función compuesta es $(f(g(x)))' = f'(g(x))g'(x)$

Estas reglas funcionarán a la perfección y te ayudarán a encontrar la derivada de cualquier función básica.

¿cómo usar las reglas de la derivada?

Paso 1: Identifique la función f(x) que desea derivar, simplifique si es necesario
Paso 2: Intenta dividir la función en partes derivadas más pequeñas, usando la linealidad
Paso 3: Dependiendo de la estructura de la función f(x), use cualquiera de las reglas disponibles (producto, cociente y regla de la cadena), y tenga en cuenta que es posible que deba aplicar muchas de las reglas consecutivamente)

Por lo general, terminarás con una combinación de varias reglas de diferenciación, hasta que llegues al punto en el que encuentres una función elemental, de la que ya sabes cómo diferenciar.

¿puedo resolver todas las derivadas?

Decir que usar reglas de diferenciación puede llevarte a resolver TODAS las derivadas puede ser una exageración. Podrá resolver la MAYORÍA de las derivadas, y ciertamente todas las básicas, pero hay funciones que tienen un comportamiento menos intuitivo que podría definirse, aunque normalmente no se tratan en los cursos de Cálculo básico.

En lo que a funciones básicas se refiere, la mayoría de ellas estarán diferenciadas sin problema.

A derivada de la regla del producto , derivada de la regla del cociente o derivada de la regla de la cadena es poco probable que estén aislados, y probablemente vendrán en una secuencia de varias reglas que deben usarse juntas.

Ejemplo: reglas derivadas

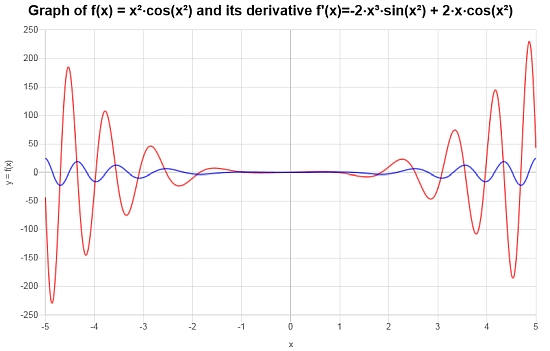
Usando reglas básicas de derivadas, calcule la siguiente derivada: $\frac{d}{dx}\left( x^2 \cos(x^2) \right)$

Solución: Consideremos la siguiente función dada para la cual se debe calcular la derivada $\displaystyle f(x)=x^2\cos\left(x^2\right)$

La función no necesita simplificación, por lo que podemos pasar directamente a calcular su derivada:

$ \displaystyle \frac{d}{dx}\left(x^2\cos\left(x^2\right)\right)$

Now, using the Product Rule: $\frac{d}{dx}\left( x^2\cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)$

We have to use the Chain Rule: $\frac{d}{dx}\left( \cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right)\cdot \left(-\sin\left(x^2\right)\right)$ and using the Power Rule for polynomial terms: $\frac{d}{dx}\left( x^2 \right) = 2x$

$ \displaystyle = \,\,$

$\displaystyle \left(2x\right) \cos\left(x^2\right)+x^2 \cdot 2x\cdot \left(-\sin\left(x^2\right)\right)$

so then we get

$ \displaystyle = \,\,$

$\displaystyle x^2\cdot 2x\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)$

By reordering some of the numerical values, and then grouping the terms with $x$ in the term $x^2\cdot 2x$

$ \displaystyle = \,\,$

$\displaystyle 2x^3\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)$

But we get $(2x^3) \cdot (-\sin\left(x^2\right)) = -2x^3\sin\left(x^2\right) = -2x^3\sin\left(x^2\right)$, due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

$ \displaystyle = \,\,$

$\displaystyle -2x^3\sin\left(x^2\right)+2x\cos\left(x^2\right)$

And finally, grouping the terms together

$ \displaystyle = \,\,$

$\displaystyle -2\left(x^2\sin\left(x^2\right)-\cos\left(x^2\right)\right)x$

A continuación se muestra la gráfica correspondiente de la función y su derivada:

Ejemplo: más reglas derivadas

Calcule la siguiente derivada: $\frac{d}{dx}\left( x \cos(x^2+1) \right)$ utilizando las reglas básicas de derivadas.

Solución: Ahora, la tarea en cuestión es diferenciar la función $\displaystyle f(x)=x\cos\left(x^2+1\right)$

$ \displaystyle \frac{d}{dx}\left(x\cos\left(x^2+1\right)\right)$

In this case, we have to use the Product Rule: $\frac{d}{dx}\left( x\cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)$

The Chain Rule for this composition: $\frac{d}{dx}\left( \cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)$

By linearity, we know $\frac{d}{dx}\left( x^2+1 \right) = \frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)$, so plugging that in:

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)$

The derivative of a constant is 0, so then:

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)$

Using the Power Rule for polynomial terms: $\frac{d}{dx}\left( x^2 \right) = 2x$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(2x\right)\cdot \left(-\sin\left(x^2+1\right)\right)$

which then leads to

$ \displaystyle = \,\,$

$\displaystyle x\cdot 2x\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)$

Putting together the numerical values and grouping the terms with $x$ in the term $x\cdot 2x$

$ \displaystyle = \,\,$

$\displaystyle 2x^2\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)$

Observe that $(2x^2) \cdot (-\sin\left(x^2+1\right)) = -2x^2\sin\left(x^2+1\right) = -2x^2\sin\left(x^2+1\right)$, due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

$ \displaystyle = \,\,$

$\displaystyle -2x^2\sin\left(x^2+1\right)+\cos\left(x^2+1\right)$

So then we get

$ \displaystyle = \,\,$

$\displaystyle -2x^2\cos\left(x^2\right)\sin\left(1\right)-2x^2\cos\left(1\right)\sin\left(x^2\right)+\cos\left(1\right)\cdot \cos\left(x^2\right)-\sin\left(1\right)\cdot \sin\left(x^2\right)$

Ejemplo de reglas derivadas

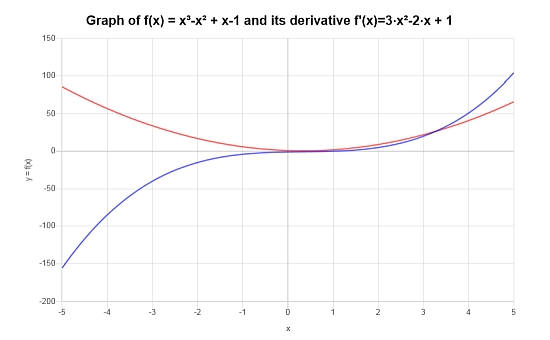
Para la función $ f(x) = (x-1)(x^2+1) $, usa reglas de derivadas para encontrar su derivada.

Solución: Para este ejemplo final, necesitamos diferenciar: $\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)$.

Paso Inicial: En este caso, primero necesitamos expandir la función dada $\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right) $, y para hacerlo, llevamos a cabo los siguientes pasos de simplificación:

$ \displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)$

Note that $(x-1) \cdot (x^2+1) = x\cdot x^2+x-x^2-1^2 = x^3-x^2+x-1$, due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

$ \displaystyle = \,\,$

$\displaystyle x^3-x^2+x-1$

Después de expandir la función, podemos proceder al cálculo de la derivada:

$ \displaystyle \frac{d}{dx}\left(x^3-x^2+x-1\right)$

By linearity, we know $\frac{d}{dx}\left( x^3-x^2+x-1 \right) = \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)$, so plugging that in:

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)$

The derivative of a constant is 0, so then:

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)$

We know that $\frac{d}{dx}\left(x\right) = 1$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+1$

Using the Power Rule for polynomial terms: $\frac{d}{dx}\left( x^2 \right) = 2x$ and $\frac{d}{dx}\left( x^3 \right) = 3x^2$

$ \displaystyle = \,\,$

$\displaystyle 3x^2-2x+1$

Gráficamente, así es como se ven la función y su derivada:

Más calculadoras de derivadas

Una de las cosas mágicas de la diferenciación es que puedes encuentra la derivada de cualquier función usando algunas reglas básicas y simples, incluyendo la Regla Del Producto , Regla Del Cociente y naturalmente, la regla de la cadena . Este pequeño arsenal suele ser suficiente para calcular cualquier derivado que necesite

La diferenciación y la integración son los carriles principales en Cálculo, sin ninguna disputa, ya que son el centro de tantas aplicaciones, en todos los aspectos de la ciencia. De tasas relacionadas a diferenciación implícita , con Derivadas parciales en Física y Economía