Calculadoras Cálculo

Calculadora de aproximación lineal

Instrucciones: Use esta calculadora para calcular la aproximación lineal para una función dada en un punto dado que proporcione, mostrando todos los pasos. Escriba la función y el punto en el cuadro de formulario a continuación.

Calculadora de aproximación lineal

Este calculadora de linealización permitirá calcular la aproximación lineal, también conocida como Linea tangente para cualquier función válida dada, en un punto válido dado.

Debe proporcionar una función válida como, por ejemplo, f(x) = x*sin(x), o f(x) = x^2 - 2x + 1, o cualquier función válida que sea diferenciable, y un punto $x_0$ donde la función está bien definida. Este punto puede ser cualquier expresión numérica válida, como 1/3, por ejemplo.

Una vez que proporcione una función y un punto válidos, haga clic en "Calcular" y se le mostrarán todos los cálculos.

Aproximación lineal o de primer orden busca una aproximación de la función dada por una línea, en un punto dado $x_0$. Naturalmente, para las curvas, una aproximación lineal será aproximada, aunque la idea principal es que la aproximación sea precisa para puntos cercanos a $x_0$.

Aproximación lineal

La idea es encontrar una línea que pase por el punto $(x_0, f(x_0))$ y "apenas toque" la función $f(x)$. La definición matemática formal de 'apenas tocando' está dada por la idea de Linea tangente , para lo cual necesitamos Calcular la derivada de la función

De hecho, la fórmula para la aproximación lineal en el punto $x_0$ depende de la derivada $f'(x_0)$, como sigue

\[\displaystyle y = f(x_0) + f'(x_0) (x - x_0) \]

Este fórmula de aproximación lineal esencialmente define la ecuación de una línea que pasa por el punto $(x_0, f(x_0))$, por lo que se denomina "aproximación lineal", ya que define una función lineal que coincide con $f(x)$ en el punto $x_0$, y es muy cercana a $f(x)$ para valores de $x$ que están cerca de $x_0$.

Pasos para encontrar la aproximación lineal

Paso 1: Necesitas tener una función dada f(x) y un punto x0. La función debe ser derivable en x0
Paso 2: Calcule f(x0) y f'(x0), que son la función y la derivada de la función f en el punto x0
Paso 3: Defina la aproximación lineal como y = f(x_0) + f'(x_0) (x - x_0), que es la fórmula de linealización presentada anteriormente

Esta línea, $y = f(x_0) + f'(x_0) (x - x_0)$ representa la aproximación de primer orden, también conocida como aproximación lineal local.

Enlace con recta tangente

Como probablemente ya sospechaste, la aproximación lineal es la misma que la Linea tangente en el punto dado. Entonces, calcular la aproximación lineal es exactamente lo mismo que calcular la recta tangente

Otro nombre para lo mismo es aproximación de primer orden, o aproximación de línea tangente, que también son nombres comúnmente utilizados en cálculo.

Aproximación diferencial y lineal

Otro concepto común es el de diferencial, que está estrechamente ligado al de aproximación lineal, y es simplemente una derivación del mismo. De hecho, el diferencial (o diferencia finita) se define como $\Delta y = y - f(x_0)$. Entonces, con base en la fórmula de aproximación de primer orden, la fórmula para el diferencial es

\[\displaystyle \Delta y = y - f(x_0) = f'(x_0) (x - x_0) = f'(x_0) \Delta x \]

Naturalmente, esto se parece exactamente a la fórmula de aproximación lineal, excepto que el término $f(x_0$ se pasa a la izquierda.

Ejemplo: cálculo de aproximación de primer orden.

Considere lo siguiente: $f(x) = x^2 - 2x + 3$, encuentre su aproximación de primer orden en $x_0 = 1$.

Solución: La función que se ha proporcionado es $\displaystyle f(x)=x^2-2x+3$, y necesitamos encontrar la aproximación lineal alrededor del punto x = 1. Entonces, primero necesitamos la derivada.

$ \displaystyle \frac{d}{dx}\left(x^2-2x+3\right)$

By linearity: $\frac{d}{dx}\left( x^2-2x+3 \right) = \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(3\right)$, so plugging that in:

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(3\right)$

The derivative of a constant is 0, so then:

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(2x\right)$

Directly: $\frac{d}{dx}\left( 2x \right) = 2$ and using the Power Rule for polynomial terms: $\frac{d}{dx}\left( x^2 \right) = 2x$

$ \displaystyle = \,\,$

$\displaystyle 2x-2$

Aproximación Lineal : La ecuación para la aproximación lineal que buscamos en el punto $x_0 = 2$ viene dada por la siguiente fórmula

\[y = y_0 + f'(x_0)(x - x_0) \]

Note que por definición $\displaystyle y_0 = f(x_0)$, lo que implica que necesitamos reemplazar la función en el punto $x_0 = 2$ :

\[y_0 = f(x_0) = f\left(2\right) = 2^2-2\cdot 2+3 = 3\]

Hacemos lo mismo, pero ahora para la derivada en el punto $x_0 = 2$, entonces

\[f'(x_0) = f'\left(2\right) = 2\cdot 2-2 = 2 \]

Ahora con esto, volvemos a la fórmula de aproximación lineal:

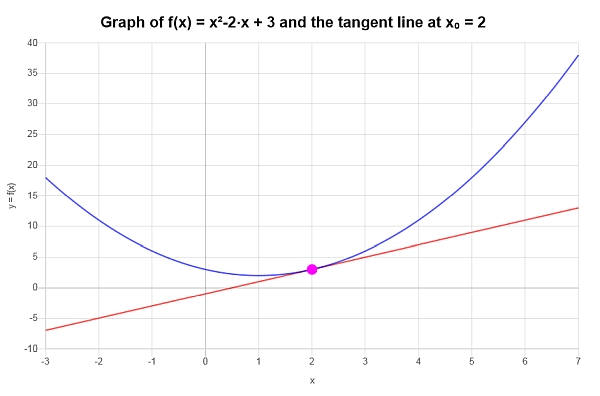
\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 3+2\left(x-2\right) = 2x-1 \]

Conclusión : Concluimos que la aproximación lineal para $\displaystyle f(x)=x^2-2x+3$ en $x_0 = 2$ está dada por:

\[y = 2x-1 \]

Gráficamente:

Ejemplo: más aproximación de primer orden

Para la función: $f(x) = x \sin(x)$ y el punto $x_0 = 2$, encuentre la aproximación de primer orden correspondiente.

Solución: En este caso, la función que necesitamos trabajar es: $\displaystyle f(x)=x\sin\left(x\right)$.

Ahora calculamos su derivada:

$ \displaystyle \frac{d}{dx}\left(x\sin\left(x\right)\right)$

Using the Product Rule: $\frac{d}{dx}\left( x\sin\left(x\right) \right) = \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)$

Directly differentiating: $\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \cos\left(x\right)$

Finally, simplifying

$ \displaystyle = \,\,$

$\displaystyle x\cos\left(x\right)+\sin\left(x\right)$

Aproximación Lineal : La ecuación de la aproximación lineal es:

\[y = y_0 + f'(x_0)(x - x_0) \]

donde $\displaystyle y_0 = f(x_0)$, entonces calculamos:

\[y_0 = f(x_0) = f\left(2\right) = 2\sin\left(2\right)\]

Para la derivada en $x_0 = 2$ encontramos que:

\[f'(x_0) = f'\left(2\right) = 2\cos\left(2\right)+\sin\left(2\right) \]

Ahora estamos listos para volver a colocarlos en la fórmula de aproximación de primer orden:

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 2\sin\left(2\right)+2\cos\left(2\right)+\sin\left(2\right)\left(x-2\right) = 2x\cos\left(2\right)+x\sin\left(2\right)-4\cos\left(2\right) \]

Conclusión : Se concluye que la aproximación lineal de $\displaystyle f(x)=x\sin\left(x\right)$ en el punto dado $x_0 = 2$ se calcula como:

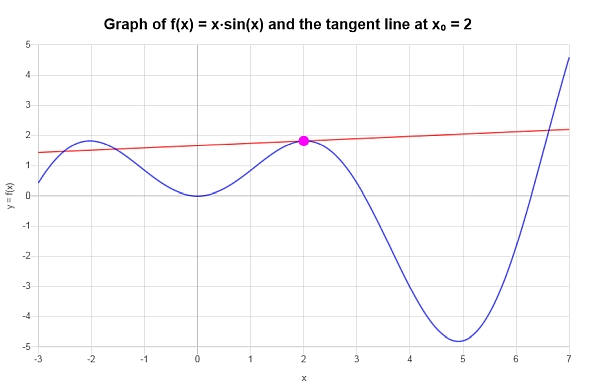
\[y = 2x\cos\left(2\right)+x\sin\left(2\right)-4\cos\left(2\right) \]

Gráficamente obtenemos el siguiente gráfico:

Ejemplo: cálculo de aproximación lineal

Calcule la aproximación de primer orden para $ f(x) = \frac{\sin(x)}{x}$ en $x = \frac{\pi}{4}$.

Solución: Se ha proporcionado la siguiente función: $\displaystyle f(x)=\frac{\sin\left(x\right)}{x}$, para la cual necesitamos calcular su derivada.

La función ya vino simplificada, por lo que podemos proceder directamente a calcular su derivada:

$ \displaystyle \frac{d}{dx}\left(\frac{\sin\left(x\right)}{x}\right)$

Using the Quotient Rule: $\frac{d}{dx}\left( \frac{\sin\left(x\right)}{x} \right) = \frac{x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}$

$ \displaystyle = \,\,$

$\displaystyle \frac{x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}$

We know that $\frac{d}{dx}\left(x\right) = 1$

$ \displaystyle = \,\,$

$\displaystyle \frac{x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)}{x^2}$

Directly differentiating: $\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{x \cdot \cos\left(x\right)-\sin\left(x\right)}{x^2}$

Therefore, we get

$ \displaystyle = \,\,$

$\displaystyle \frac{x\cos\left(x\right)-\sin\left(x\right)}{x^2}$

Aproximación De Primer Orden : La ecuación para la aproximación de primer orden correspondiente para la función dada $\displaystyle f(x)=\frac{\sin\left(x\right)}{x}$ en el punto dado $x_0 = \frac{\pi}{4}$ viene dada por lo siguiente:

\[y = y_0 + f'(x_0)(x - x_0) \]

Conectando los valores correspondientes:

\[y_0 = f(x_0) = f\left(\frac{\pi}{4}\right) = \frac{\sin\left(\frac{\pi{}}{4}\right)}{\frac{\pi{}}{4}} = \frac{2\sqrt{2}}{\pi{}}\] \[f'(x_0) = f'\left(\frac{\pi}{4}\right) = \frac{\cos\left(\frac{\pi{}}{4}\right)}{\frac{\pi{}}{4}}-\frac{\sin\left(\frac{\pi{}}{4}\right)}{\left(\frac{\pi{}}{4}\right)^2} = \frac{2\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}}{\pi{}^2} \]

Así que ahora podemos poner esto en la fórmula:

\[y = y_0 + f'(x_0)(x - x_0) \] \[\Rightarrow y = \frac{2\sqrt{2}}{\pi{}}+\frac{2\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}}{\pi{}^2}\left(x-\frac{1}{4}\pi{}\right) = -\frac{1}{2}\sqrt{2}+\frac{2\sqrt{2}x}{\pi{}}+\frac{4\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}x}{\pi{}^2} \]

Conclusión : Podemos concluir, por lo tanto, que la aproximación de primer orden para la función dada $\displaystyle f(x)=\frac{\sin\left(x\right)}{x}$ en el punto dado $x_0 = \frac{\pi}{4}$ está dada por

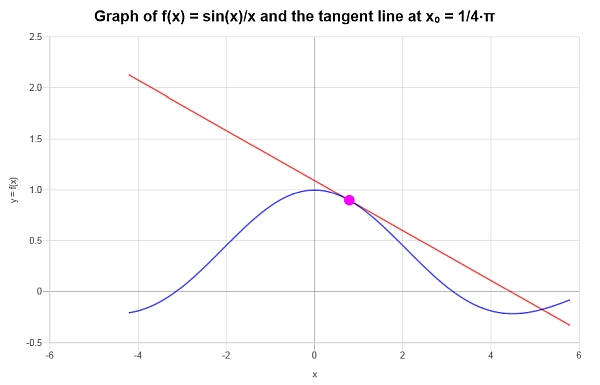
\[y = -\frac{1}{2}\sqrt{2}+\frac{2\sqrt{2}x}{\pi{}}+\frac{4\sqrt{2}}{\pi{}}-\frac{8\sqrt{2}x}{\pi{}^2} \]

De forma gráfica se obtiene lo siguiente:

Más calculadoras de derivadas

Aparte de esto calculadora de linealización , puedes encontrar muchos que hacen cosas diferentes basadas en derivados. La diferenciación es una operación crucial en Cálculo, Física, Ingeniería y Economía, con un amplio espectro de aplicaciones.

También hay una forma de realizar una aproximación lineal para más variables, esto es, por ejemplo, para una función \f(x, y)\), en cuyo caso la fórmula de aproximación lineal se convierte en $f(x, y) = f(x_0, y_0) + \frac{\partial f}{\partial x}(x_0, y_0)(x-x_0) + \frac{\partial f}{\partial y}(x_0, y_0)(y-y_0)$, entonces en este caso, para encontrar la linealización necesitamos usar Derivadas parciales .

Encontrar la linealización de una función no es lo único que puedes hacer con las derivadas. La diferenciación es una operación relativamente fácil con reglas simples como la Regla Del Producto , la regla del cociente y el Cadena De Reglas eso hace que el cálculo de derivados sea una operación relativamente sencilla.

Aunque se supone que es simple, es una buena idea usar un calculadora de derivadas para obtener todos los pasos que se muestran, con una mención clara de todos los Reglas Derivadas usado.