Calculadora de periodos y frecuencias

Cuando se trata de funciones periódicas, hay algunos parámetros cruciales que deben calcularse, y estos son el período (\(P\)) y la frecuencia (\(f\)).

El periodo \(P\) de una función periódica corresponde al número que cumple la siguiente propiedad:

\[f(x+P) = f(x)\]

para todos los valores de \(x\). Observe que no todas las funciones tienen un punto. Los que lo hacen se llaman funciones periódicas .

Período de algunas funciones comunes

Las funciones trigonométricas son ejemplos de funciones periódicas. Por ejemplo, si consideramos la función, \(f(x) = \sin x\), su período es \(2\pi\), como se muestra en el siguiente gráfico:

Para \(\cos x\) también tenemos que el período es \(2\pi\). Mira el gráfico a continuación:

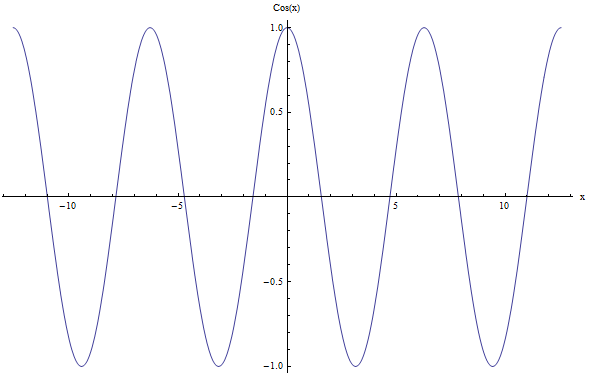
Período de otras funciones trigonométricas

Recuerda que la función cosecante \(\csc x\) es la inversa de \(\sin x\), esto es \(\csc x = \frac{1}{\sin x}\), entonces el período de \(\csc x\) también es \(2\pi\).

De manera similar, la función secante \(\sec x\) es la inversa de \(\cos x\), esto es \(\sec x = \frac{1}{\cos x}\), entonces el período de \(\sec x\) es \(2\pi\) también.

¿Qué tal la tangente? La función tangente \(\tan x\) es ligeramente diferente porque su período es \(\pi\). De hecho, su gráfico se ve diferente a los del seno y el coseno, pero la tangente también es periódica. Una diferencia es que \(\tan x\) tiene discontinuidades. Échale un vistazo:

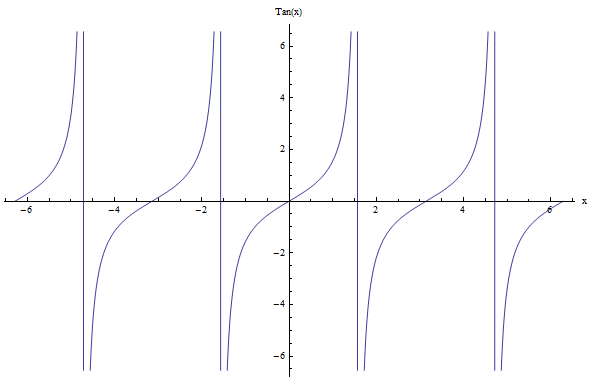
De manera similar que antes, la función cotangente \(\cot x\) es la inversa de \(\tan x\), con \(\cot x = \frac{1}{\tan x}\), entonces el período de \(\cot x\) también es \(\pi\).

Cálculo de la frecuencia

Otro elemento importante a considerar para la función periódica es la frecuencia (\(f\)), que se calcula en términos del período \(P\) como:

\[f = \frac{1}{P}\]

Entonces la frecuencia es la inversa del período. Y viceversa, el período es el inverso de la frecuencia.

Por ejemplo, ¿cuál es la frecuencia de \(\sin x\)? Siguiendo la fórmula anterior, ya que sabemos que para seno el periodo es \(P = 2\pi\):

\[f = \frac{1}{P} = \frac{1}{2\pi} \approx 0.1592\]

Esta calculadora también calculará la amplitud, el cambio de fase y el cambio vertical si la función está definida correctamente. Esos parámetros determinan bastante el comportamiento de la función trigonométrica.

Si necesita graficar una función trigonométrica, debe usar esto generador de gráficos trigonométricos .