Más acerca de esta calculadora de producto escalar

Esta calculadora le permitirá calcular el producto punto de dos vectores, mostrando todos los pasos. Todo lo que necesita hacer es escribir los vectores y hacer clic en 'Calcular'.

El producto de puntos tiene MUCHAS aplicaciones en álgebra lineal, para calcular proyecciones y evaluar la perpendicularidad de los vectores.

De hecho, geométricamente hablando, un producto punto que es igual a cero implica que los dos vectores son perpendicular .

La fórmula del producto escalar

Entonces, ¿cómo se calcula el producto escalar? El producto escalar es una operación realizada para dos vectores \(x\) y \(y\), y el resultado de la operación es un escalar. La fórmula para el producto escalar se muestra a continuación:

\[ \langle x, y \rangle = \sum_{i=1}^n x_i y_i \]

El producto punto \(\langle x,y \rangle\) se conoce con diferentes nombres, y también se le llama, producto Interno o producto escalar . Esencialmente, el producto escalar es un producto matriz si consideramos \(x \in \mathbb{R}^n\) y \(y \in \mathbb{R}^n\), entonces el producto escalar se define como:

\[ \langle x, y \rangle = \sum_{i=1}^n x_i y_i = x^t \cdot y \]

Esta fórmula es fácil de recordar a diferencia del caso del producto cruz . Es fácil calcular el producto escalar a mano, como en el caso del producto escalar, multiplicas el componente correspondiente y luego los sumas.

Aplicaciones de productos punto

Algunos usos del producto escalar son súper claros y prácticos: El Calculadora de producto escalar y el ángulo. De hecho, el punto o producto interior también tiene una fuerte motivación geométrica. Ciertamente, una expresión alternativa para ello es

\[ \langle x, y \rangle = \|x\| \|y\| \cos \theta \]

donde \(\|x\|\) es la norma (longitud) de \(x\), \(\|y\|\) es la norma (longitud) de \(y\) y \(\theta\) es el ángulo entre \(x\) y \(y\).

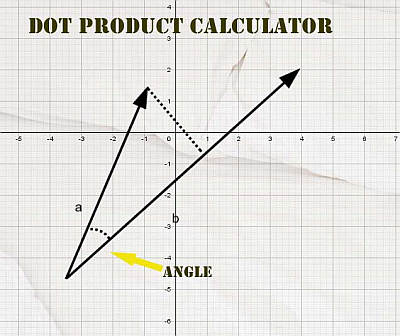
Producto escalar con cálculo de ángulo

Una consecuencia directa de la definición de producto escalar es que puedes usarlo para calcular el ángulo entre dos vectores, usando la siguiente fórmula:

\[\cos \theta = \displaystyle \frac{ \langle x, y \rangle}{\|x\| \|y\| } \]

y si resolvimos para \(\theta\):

\[ \theta = \arccos\left( \displaystyle \frac{ \langle x, y \rangle}{\|x\| \|y\| } \right) \]

El producto escalar y el producto cruz

Una operación relacionada para dos vectores es la producto cruz , aunque tiene un ahora diferente ya que su salida es un vector y no un escalar.

Más calculadoras de álgebra

Puede navegar y ver más calculadoras de álgebra en nuestro calculadoras y calculadoras de álgebra sección.

Calculadoras de producto punto y producto cruz , entre muchos otros tienen un alto grado de aplicabilidad en el Álgebra Lineal y la Geometría.

Aunque algunos sistemas informáticos pueden mostrarle las respuestas, nuestras calculadoras le mostrarán los pasos para que comprenda de dónde vienen las cosas.