Solvers Cálculo

Regla del cociente

Instrucciones: Use esta calculadora de la regla del cociente para encontrar la derivada de la función que involucra los cocientes que proporciona, mostrando todos los pasos. Escriba la función en el cuadro de formulario a continuación.

La regla del cociente

Esta calculadora te permitirá usar la regla del cociente para una función que involucre un cociente, mostrando todos los pasos del proceso. Todo lo que necesita proporcionar es una función diferenciable válida. Esta función necesita involucrar al menos un cociente para que la regla del cociente sea aplicable.

Un ejemplo de una función válida sería f(x) = (x^2 + 2x + 1)/(x^2-1), o algo así como f(x) = sin(x)/x, etc.

Una vez que se proporciona una función válida que involucra cocientes, debe hacer clic en el botón "Calcular" para que se muestren los pasos del cálculo.

Junto con Regla Del Producto y Cadena De Reglas el Regla Del Cociente es uno de los básicos más importantes Reglas Derivadas .

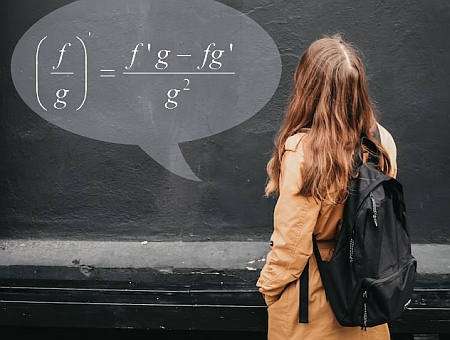
Fórmula de la regla del cociente

En términos simples, el Regla Del Cociente le ayuda a calcular la derivada de un cociente, utilizando el conocimiento de las funciones individuales y sus derivadas. La fórmula de la regla del cociente es:

\[\displaystyle \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \displaystyle \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} \]

¿cuáles son los pasos para usar la regla del cociente?

Paso 1: Identifica claramente las funciones f(x) y g(x) que van en el numerador y denominador del cociente
Paso 2: Simplifica cualquier término obvio que se pueda simplificar
Paso 3: Calcular las derivadas correspondientes f'(x) y g'(x)
Paso 4: Introduzca los valores encontrados en el Paso 3 en la fórmula $\displaystyle \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \displaystyle \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} $

Tenga en cuenta que f(x) y g(x) aún pueden ser funciones complejas, por lo que es posible que deba usar otras reglas, como la regla de la cadena, para calcular tanto f'(x) como g'(x).

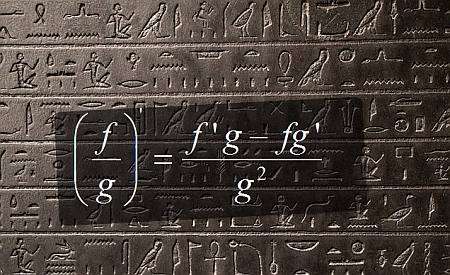
Derivada de la regla del cociente

Al calcular una derivada de la regla del cociente, está reduciendo la derivada de un cociente al conocimiento de las derivadas individuales, pero esas derivadas individuales aún pueden requerir muchos pasos con Reglas básicas de derivadas para ser resuelto.

Es por eso que la diferenciación se considera una operación 'sencilla', pero aún así, debe organizarse lo suficiente y realizar un seguimiento de todas las piezas que surgen al descomponer con reglas derivadas, y luego proceder con las piezas más pequeñas que pueden requerir más reglas de diferenciación para ser aplicado.

Entonces, puede terminar con un proceso iterativo, pero se garantiza que terminará en algún punto al profundizar en cada parte más pequeña, hasta que encuentre una derivada elemental, como polinomio o un derivada trigonométrica .

Regla del cociente en la diferenciación

El papel del regla del cociente en la diferenciación es bastante importante, una buena razón por la que querrás usar una calculadora para ello. En términos algebraicos, la regla del cociente podría considerarse más complicada que la regla del producto, y podría ser cierta en muchos casos, pero en última instancia depende de la complejidad de las funciones en el numerador y el denominador.

Ejemplos de la regla del cociente

Considere la función: $f(x) = \frac{x^2+1}{x-2}$, encuentre su derivada.

Solución: Para este ejemplo, necesitamos analizar la función $\displaystyle f(x)=\frac{x^2+1}{x-2}$, en términos de encontrar su derivada.

$ \displaystyle \frac{d}{dx}\left(\frac{x^2+1}{x-2}\right)$

By using the Quotient Rule: $\frac{d}{dx}\left( \frac{x^2+1}{x-2} \right) = \frac{\left(x-2\right) \cdot \frac{d}{dx}\left(x^2+1\right)-\left(x^2+1 \right) \cdot \frac{d}{dx}\left(x-2\right)}{\left(x-2\right)^2}$

$ \displaystyle = \,\,$

$\displaystyle \frac{\left(x-2\right) \cdot \frac{d}{dx}\left(x^2+1\right)-\left(x^2+1 \right) \cdot \frac{d}{dx}\left(x-2\right)}{\left(x-2\right)^2}$

By linearity, we know $\frac{d}{dx}\left( x-2 \right) = \frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(2\right)$ and $\frac{d}{dx}\left( x^2+1 \right) = \frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)$, so plugging that in:

$ \displaystyle = \,\,$

$\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\right)-\left(x^2+1 \right) \left(\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(2\right)\right)}{\left(x-2\right)^2}$

Since the derivative of a constant is 0, we get that:

$ \displaystyle = \,\,$

$\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)\right)-\left(x^2+1 \right) \left(\frac{d}{dx}\left(x\right)\right)}{\left(x-2\right)^2}$

We already know that $\frac{d}{dx}\left(x\right) = 1$

$ \displaystyle = \,\,$

$\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)\right)-\left(x^2+1 \right)}{\left(x-2\right)^2}$

In this case we use the Power Rule for polynomial terms: $\frac{d}{dx}\left( x^2 \right) = 2x$

$ \displaystyle = \,\,$

$\displaystyle \frac{\left(x-2\right) \left(2x\right)-\left(x^2+1 \right)}{\left(x-2\right)^2}$

and then we get

$ \displaystyle = \,\,$

$\displaystyle \frac{2x\left(x-2\right)-\left(x^2+1\right)}{\left(x-2\right)^2}$

Note that $(2x) \cdot (x-2) = 2x^2-2\cdot 2x = 2x^2-4x$, as we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

$ \displaystyle = \,\,$

$\displaystyle \frac{2x^2-4x-\left(x^2+1\right)}{\left(x-2\right)^2}$

Removing unnecessary parentheses and multiplying the terms by $-1$

$ \displaystyle = \,\,$

$\displaystyle \frac{2x^2-4x-x^2-1}{\left(x-2\right)^2}$

Aggregating those terms with $x^2$

$ \displaystyle = \,\,$

$\displaystyle \frac{-4x+\left(-1+2\right)x^2-1}{\left(x-2\right)^2}$

Putting together the numerical values and operating the terms that were grouped with $x^2$

$ \displaystyle = \,\,$

$\displaystyle \frac{-4x+x^2-1}{\left(x-2\right)^2}$

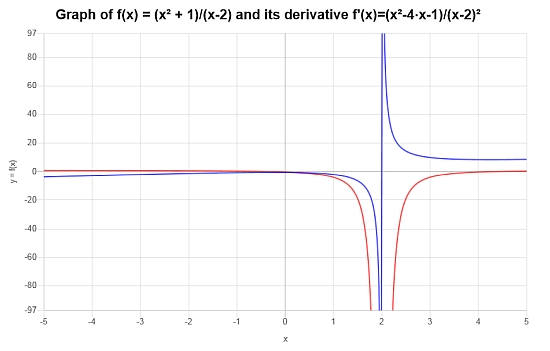
Conclusión : Encontramos que la derivada de la función dada es:

\[f'(x) = \frac{x^2-4x-1}{\left(x-2\right)^2}\]

Entonces, la representación gráfica de la función y su derivada es $[-5, 5]$:

Ejemplo: cálculo de la regla del cociente

Ahora considere $f(x) = \frac{x}{\sin(x)}$, encuentre su derivada usando la regla del cociente.

Solución: Para este segundo ejemplo, la función que nos interesa es $\displaystyle f(x)=\frac{x}{\sin\left(x\right)}$. Diferenciémoslo usando la regla del cociente.

$ \displaystyle \frac{d}{dx}\left(\frac{x}{\sin\left(x\right)}\right)$

Using the Quotient Rule: $\frac{d}{dx}\left( \frac{x}{\sin\left(x\right)} \right) = \frac{\sin\left(x\right) \cdot \frac{d}{dx}\left(x\right)-x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}$

$ \displaystyle = \,\,$

$\displaystyle \frac{\sin\left(x\right) \cdot \frac{d}{dx}\left(x\right)-x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}$

We already know that $\frac{d}{dx}\left(x\right) = 1$

$ \displaystyle = \,\,$

$\displaystyle \frac{\sin\left(x\right) -x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}$

Directly differentiating: $\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{\sin\left(x\right) -x\cdot \cos\left(x\right)}{\sin\left(x\right)^2}$

so then we get that

$ \displaystyle = \,\,$

$\displaystyle \frac{\sin\left(x\right)-x\cos\left(x\right)}{\sin\left(x\right)^2}$

By reorganizing/simplifying/expanding the terms that are amenable to

$ \displaystyle = \,\,$

$\displaystyle \frac{-\left(x\cos\left(x\right)-\sin\left(x\right)\right)}{\sin\left(x\right)^2}$

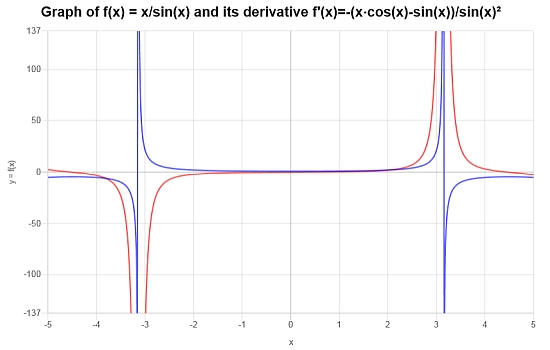
Conclusión : La conclusión es que, en base al cálculo anterior, la derivada está dada por:

\[f'(x) = \frac{-\left(x\cos\left(x\right)-\sin\left(x\right)\right)}{\sin\left(x\right)^2}\]

Gráficamente podemos ver la función (en azul) y su derivada (en rojo):

Más ejemplos de reglas de cociente

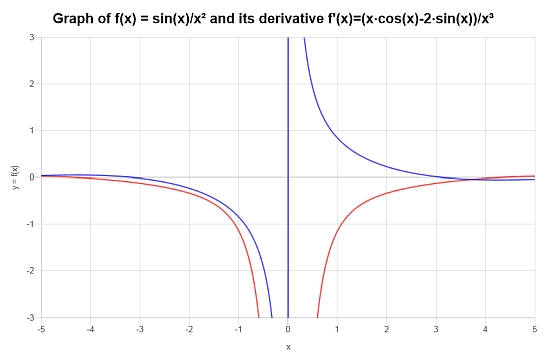
Finalmente, considere la función: $f(x) = \frac{\sin(x)}{x^2}$, encuentre su derivada.

Solución: Para este ejemplo final de la regla del cociente, trabajamos con la función $\displaystyle f(x)=\frac{\sin\left(x\right)}{x^2}$. .

$ \displaystyle \frac{d}{dx}\left(\frac{\sin\left(x\right)}{x^2}\right)$

The Quotient Rule applies: $\frac{d}{dx}\left( \frac{\sin\left(x\right)}{x^2} \right) = \frac{\left(x^2\right) \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x^2\right)}{\left(x^2\right)^2}$

$ \displaystyle = \,\,$

$\displaystyle \frac{\left(x^2\right) \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x^2\right)}{\left(x^2\right)^2}$

We use the Power Rule for polynomial terms: $\frac{d}{dx}\left( x^2 \right) = 2x$ and directly differentiating: $\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)$

$ \displaystyle = \,\,$

$\displaystyle \frac{\left(x^2\right) \cdot \cos\left(x\right)-\sin\left(x\right)\cdot 2x}{\left(x^2\right)^2}$

which then leads to

$ \displaystyle = \,\,$

$\displaystyle \frac{\cos\left(x\right)\cdot x^2-\sin\left(x\right)\cdot 2x}{x^4}$

By simplifying and regrouping terms

$ \displaystyle = \,\,$

$\displaystyle \frac{x\cos\left(x\right)-2\sin\left(x\right)}{x^3}$

Conclusión : Para la función dada, su derivada es:

\[f'(x) = \frac{x\cos\left(x\right)-2\sin\left(x\right)}{x^3}\]

El siguiente gráfico muestra la situación de $f$ y $f'$:

Más calculadoras de derivadas

En Cálculo usted encontrar derivados dondequiera que mires. Hay miles de aplicaciones que los involucran convirtiéndolos en las herramientas más importantes para la ciencia y la ingeniería.

Tendrás que aprender sobre diferenciación implícita para diferentes aplicaciones muchas veces involucrando tasas relacionadas, o en cálculo multivariado que le interesará encontrar derivadas parciales .

En general, encontrará que su vida es más fácil al tratar con derivados si es capaz de manejar adecuadamente los más comunes. Reglas Derivadas , incluyendo el Cadena De Reglas , así como el Regla Del Producto y Regla Del Cociente .