Calculadora diferencial
Instrucciones: Use esta calculadora diferencial para encontrar la diferencial de una función que proporcione, en un punto dado que proporcione, mostrando todos los pasos. Escriba la función y el punto en el cuadro de formulario a continuación.
Calculadora diferencial
Esta calculadora te permitirá calcular el diferencial de una función que proporciones, en un punto que proporciones, mostrando todos los pasos del proceso.
La función que proporcione puede ser cualquier función diferenciable válida como f(x) = x^2 + 2x, o f(x) = x^2*sin(x), solo por mencionar dos ejemplos.
Luego, cuando haya proporcionado la función y el punto para el cálculo diferencial, simplemente haga clic en "Calcular" para que se muestren todos los pasos del proceso.
La idea de Diferencial está estrechamente con el de la línea tangente y Aproximación Lineal , ya que el diferencial mide precisamente la variación de y, a lo largo de la Linea tangente en el punto dado.
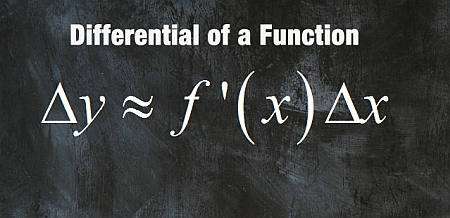
¿qué es un diferencial?
En cálculo diferencial, la idea es que las derivadas te den información sobre la tasa de cambio instantánea de una función en un punto dado.
El concepto de diferencial utiliza el tasa de cambio determinado por la derivada en un punto dado \(x_0\) para aproximar el comportamiento de la función por su Linea tangente .
La fórmula del diferencial se basa en la idea de que
\[\displaystyle \Delta y \approx f'(x_0) \Delta x \]donde \(\Delta y = y - f(x_0)\) y \(\Delta x = x - x_0\). Para el diferencial \(dy\), definimos
\[\displaystyle dy = f'(x_0) dx \]Esta definición (floja) se basa en la idea de que la aproximación lineal y la función se aproximan al mismo comportamiento cuando \(x\) está suficientemente cerca de \(x_0\).
Pasos para calcular un diferencial
- Paso 1: Identifique la función f(x) y el punto x0 en el que desea calcular la diferencial
- Paso 2: Calcule la derivada f'(x) y evalúela en x0, de modo que obtenga f'(x0). Simplificarlo, si es necesario
- Paso 3: Utilice la fórmula \(\displaystyle dy = f'(x_0) dx \)
A veces encontrará el diferencial escrito como \(\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \), como una forma de indicar que utilizará el diferencial para estimar los cambios en y, medidos por \(\Delta y\).
Calculadora diferencial dy
Usando un calculadora diferencial puede ahorrarle tiempo con el proceso de cálculo de la derivada. La idea del diferencial siempre ha sido extraña, en el sentido de que parece estar vagamente definida.
Aunque hay una forma de definir diferenciales y sus operaciones formalmente (un tema llamado Formas diferenciales), la mayoría de los matemáticos no ven una razón para que existan las diferenciales, ya que no proporcionan ninguna información nueva que la derivada o la aproximación de primer orden. no provee.
Interpretación diferencial total
La aplicación e interpretación más común del diferencial es cuando se usa en su expresión 'finita':
\[\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \]donde busca estimar la variación en y, medida por \(\Delta y\), a partir de la variación en x, medida por \(\Delta x\) y la derivada en el punto.
A veces este \(\Delta y\) se llama el variación total o diferencial total .
Consejos y trucos
No olvides que la diferencial puede tomarse como una definición teórica, \(\displaystyle dy = f'(x_0) dx \), que indica la variación infinitesimal de y provocada por una variación infinitesimal de x.
También se puede utilizar en su forma diferencial total, en la que tiene
\[\displaystyle \Delta y \approx f'(x_0)(x-x_0)\]que te dice una variación aproximada en y, cuando por un cambio en x (de \(x_0\) a \(x\)).
El centro de toda calculadora algebraica comienza con el poder de los números básicos de fracciones.
Ejemplo: calculadora diferencial
Considere la función: \(f(x) = x^2\). Encuentre su diferencial en el punto \(x_0 = 1\).
Solución: En el caso de este primer ejemplo, trabajamos con la función \(\displaystyle f(x)=x^2\), para lo cual necesitamos calcular su diferencial en el punto \(x_0 = 1\).
La función ya vino simplificada, por lo que podemos proceder directamente a calcular su derivada:
Diferencial : La fórmula de la diferencial de la función \(\displaystyle f(x)=x^2\) en el punto \(x_0 = 1\) es:
\[dy = f'(x_0)(x - x_0) \]Definimos \(\displaystyle y_0 = f(x_0)\), por lo que reemplazando el valor del punto \(x_0 = 1\) en la función lleva a:
\[y_0 = f(x_0) = f\left(1\right) = 1^2 = 1\]Además, reemplazar el valor del punto \(x_0 = 1\) en la derivada calculada conduce a:
\[f'(x_0) = f'\left(1\right) = 2\cdot 1 = 2 \]Entonces, ahora reemplazamos este valor en la fórmula diferencial para obtener:
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = 2\left(x-1\right) \]\[\Rightarrow dy = 2x-2 \]Conclusión : Por lo tanto, encontramos que la diferencial de la función \(\displaystyle f(x)=x^2\) en el punto \(x_0 = 1\) es:
\[dy = 2x-2 \]Ejemplo: cálculo diferencial
Para la función dada: \(f(x) = x^3 + 3x^2 - 2\), encuentra la diferencial en el punto \(x_0 = 2\).
Solución: Ahora, la función para la que necesitamos encontrar el diferencial es \(\displaystyle f(x)=x^3+3x^2-2\),
Cálculo Diferencial : Usamos la siguiente fórmula para el diferencial que necesitamos construir para la función dada \(\displaystyle f(x)=x^3+3x^2-2\), en el punto dado \(x_0 = \frac{1}{2}\) es:
\[dy = f'(x_0)(x - x_0) \]Observe que \(\displaystyle y_0 = f(x_0)\), lo que significa que evaluando la función en \(x_0 = \frac{1}{2}\) encontramos:
\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \left(\frac{1}{2}\right)^3+3\left(\frac{1}{2}\right)^2-2 = -\frac{9}{8}\]Entonces, obtenemos la derivada en el punto \(x_0 = \frac{1}{2}\):
\[f'(x_0) = f'\left(\frac{1}{2}\right) = 3\left(\frac{1}{2}\right)^2+6\cdot \frac{1}{2} = \frac{15}{4} \]Por lo tanto, obtenemos lo siguiente
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(\frac{15}{4}\right)\left(x-\frac{1}{2}\right) \]\[\Rightarrow dy = \frac{15}{4}x-\frac{15}{8} \]Conclusión : La conclusión final es que el diferencial que buscamos está dado por:
\[dy = \frac{15}{4}x-\frac{15}{8} \]Ejemplo diferencial
Se nos da la función: \(f(x) = \frac{\sin(x)}{x}\). Encuentre su diferencial en el punto \(x_0 = \frac{\pi}{2}\).
Solución:
Se ha proporcionado la siguiente función: \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), para lo cual necesitamos calcular su diferencial en el punto \(x_0 = \frac{\pi}{2}\).
La función ya vino simplificada, por lo que podemos proceder directamente a calcular su derivada:
Cálculo : Ahora es el momento de encontrar el diferencial asociado a \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), para el punto dado \(x_0 = \frac{\pi}{2}\). La fórmula utilizada es:
\[dy = f'(x_0)(x - x_0) \]Reemplazamos el valor del punto \(x_0 = \frac{\pi}{2}\) en la derivada calculada, lo que nos lleva a:
\[f'(x_0) = f'\left(\frac{\pi}{2}\right) = \frac{\cos\left(\frac{\pi{}}{2}\right)}{\frac{\pi{}}{2}}-\frac{\sin\left(\frac{\pi{}}{2}\right)}{\left(\frac{\pi{}}{2}\right)^2} = -\frac{4}{\pi{}^2} \]Por lo tanto, usando la fórmula diferencial:
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(-\frac{4}{\pi{}^2}\right)\left(x-\frac{1}{2}\pi{}\right) \]\[\Rightarrow dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]Conclusión : El diferencial correspondiente es:
\[dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]Otras calculadoras de diferenciación
encontrar derivados es sin duda un elemento clave en Cálculo. Los derivados proporcionan la información necesaria para comprender la tasa de cambio de funciones ya que esos tienen una conexión íntima.
Afortunadamente, encontrar derivadas es un proceso sistemático (no necesariamente fácil) si sigues reglas de diferenciación . Las reglas más utilizadas son las Regla Del Producto , Regla Del Cociente y Cadena De Reglas .
lineal o aproximaciones de primer orden intenta conceptualmente aproximar una función por una línea, al menos localmente, y puede decirte mucho sobre el comportamiento de una función, cerca de cierto punto.






