Über diesen ungleichheitsgraphen

Dieser Rechner hilft Ihnen, die Lösung und das Diagramm für jede allgemeine Ungleichung zu finden und zeigt alle Schritte an. Sie müssen eine gültige Ungleichung einer Variablen (x) angeben, indem Sie diese in das dafür vorgesehene Feld eingeben.

Sie können beispielsweise eine einfache lineare Ungleichung wie „3x – 1 < 1/3“ oder etwas wie „2x-x^2 <= 3/4“ angeben, was einer quadratischen Ungleichung entspricht.

Sobald Sie die Ungleichung angegeben haben, die Sie grafisch darstellen möchten, klicken Sie auf die Schaltfläche „Lösen“, um die Lösungen mit allen Schritten anzuzeigen, falls Lösungen gefunden werden konnten.

Allgemeine Gleichungen lösen und allgemeine Ungleichheiten ist im Allgemeinen eine schwierige Aufgabe, es sei denn, es handelt sich um eine spezifische Reihe von Strukturen, die einer systematischen Behandlung zugänglich sind.

Einige der wenigen Typen, die eine genaue Lösung ermöglichen, sind lineare Ungleichungen und polynomielle Ungleichungen .

Eine wichtige Art von Ungleichung, die Sie lösen möchten, sind rationale Ungleichungen, bei denen Sie einen Quotienten von Polynomen identifizieren können. Diese Ungleichungen sind interessant, da sie potenzielle Divisionen durch Null aufweisen, die angegangen werden müssen. Die Idee einer rationalen Ungleichung lässt sich leicht auf den Quotienten von Funktionen im Allgemeinen erweitern, nicht unbedingt auf Polynome

Wie man eine ungleichung grafisch darstellt

Die einfachste Antwort darauf lautet: Um eine Ungleichung grafisch darzustellen, müssen Sie wissen, wie man sie löst. Die grafische Lösung einer Ungleichung wird normalerweise als Intervall oder mehrere verbundene Intervalle auf der x-Achse dargestellt.

Vor diesem Hintergrund beginnt die grafische Darstellung einer Ungleichung damit, sie zunächst zu lösen. Dazu gehört das Finden einer Reihe von Werten in der reellen Linie, die die bereitgestellte Ungleichung erfüllen.

Sie können den Graphen möglicherweise als eigenständiges Intervall darstellen, oder Sie können die Ungleichungslösungen zusammen mit dem Graphen des Ausdrucks, der der Ungleichung zugrunde liegt, grafisch darstellen: Erinnern wir uns daran, um dies zu tun Ungleichheiten lösen , übergeben Sie alle Terme an eine Seite (wodurch Sie den zugrunde liegenden Ausdruck erhalten) und lösen eine Hilfsgleichung

Schritte zum lösen und darstellen von ungleichungen

• Schritt 1: Übergeben Sie alle Terme an eine Seite, sodass Sie auf der einen Seite einen Ausdruck und auf der anderen Seite null haben
• Schritt 2: Konstruieren Sie aus der Ungleichung (sobald alles auf der einen Seite und auf der anderen Null ist) eine Hilfsgleichung
• Schritt 3: Lösen Sie diese Gleichung mit einer Methode, die für ihre Struktur geeignet ist (verschiedene Arten von Gleichungen erfordern spezifische Techniken und Ansätze)
• Schritt 4: Basierend auf den REALEN Lösungen der Hilfsgleichungen (reale im Gegensatz zu komplexen Lösungen) konstruieren Sie Ihre kritischen Punkte und sortieren sie in aufsteigender Reihenfolge
• Schritt 5: Sie müssen auch nach Punkten suchen, an denen der Ausdruck undefiniert ist. Ein bemerkenswerter Fall hierfür tritt bei rationalen Ungleichungen auf, bei denen der Nenner ein Polynom ist und der Ausdruck dann auf den Nullstellen des Nenners undefiniert ist. Sie fügen also Nullen des Nenners zur Liste der kritischen Punkte hinzu
• Schritt 6: Mit Ihren kritischen Punkten konstruieren Sie Intervalle unter Verwendung aufeinanderfolgender kritischer Punkte (wobei -∞ und ∞ als kritische Start- und Endpunkte verwendet werden)
• Schritt 7: Analysieren Sie für jedes Intervall das Vorzeichen des Ausdrucks und prüfen Sie, ob es mit dem Vorzeichen der Ungleichung kompatibel ist. Wenn dies der Fall ist, ist das Intervall Teil der Gesamtlösung der Ungleichung

Die Verwendung kritischer Punkte für die Analyse ist von größter Bedeutung, da Sie auf diese Weise sicher sein können, dass der Ausdruck innerhalb jedes Intervalls nicht das Vorzeichen ändert, sodass sich das Problem auf die Beurteilung reduziert, ob die Ungleichung für jedes dieser kritischen Intervalle gelöst ist.

Um es etwas greifbarer zu machen, haben Sie eine Ungleichung gegeben und dann alles beiseite geschoben, sodass Sie etwas in der Form \(f(x) \le 0\) haben. Dies könnte zum Beispiel so etwas wie \(x^2 - x + 1 \le 0\) sein.

Dann nimmst du also \(f(x) \le 0\) und findest die Hilfsgleichung \(f(x) = 0\). Sie nehmen den Ausdruck \(f(x)\) und ermitteln, dass seine Nullstellen die kritischen Punkte sind. Aber Sie tun das nicht nur, sondern prüfen auch, ob \(f(x)\) irgendwo undefiniert ist (Divisionen durch Null usw.). Es kann überall definiert sein, wie im Fall \(x^2 - x + 1\), aber wenn Sie Punkte finden, an denen der Ausdruck undefiniert ist, fügen Sie ihn der Liste der kritischen Punkte hinzu.

Dann konstruieren Sie Intervalle basierend auf aufeinanderfolgenden kritischen Punkten. Für \(f(x) \le 0\) nehmen Sie als Teil der Lösungen diejenigen Intervalle, in denen der Wert des Ausdrucks negativ ist. Wenn die ursprüngliche Ungleichung \(f(x) \ge 0\) gewesen wäre, nehmen Sie als Teil der Lösungen diejenigen Intervalle, in denen der Wert des Ausdrucks positiv ist

So funktioniert dieser ungleichheitsgrapher

Unser Online-Ungleichungsgrapher kümmert sich um einen der umständlichsten Prozesse in der Grundalgebra, bei dem es darum geht, die Lösungen einer Ungleichung zu finden und sie grafisch darzustellen. Ein großer Vorteil unseres Rechners besteht darin, dass er, wenn möglich, alle Schritte anzeigt.

Zunächst löst der Grapher die Ungleichung, indem er zunächst eine geeignete Hilfsgleichung löst. Dieser Prozess erfordert die Erkennung spezifischer bekannter Strukturen, da alle Strukturen wahrscheinlich unterschiedliche Ansätze erfordern. Zum Beispiel, um eine rationale Ungleichung zu lösen (die den Quotienten zweier Polynome beinhaltet), wie zum Beispiel

\[\displaystyle \frac{x^2-2x}{x-1} \ge 4 \]

Sie benötigen einen anderen Ansatz als den, der beispielsweise zur Lösung einer quadratischen Ungleichung wie \(x^2 + 3x < 1\) verwendet wird, und dieser Rechner berücksichtigt alle diese Details

Wenn keine traditionelle oder allgemein bekannte Struktur erkannt wird, werden andere häufig verwendete Substitutionen verwendet, wie zum Beispiel \(u = \sqrt x\) oder \(u = \sin x\). Wenn nichts funktioniert, versucht der Rechner, Lösungen durch Inspektion und numerisch zu finden, um zumindest eine Vorstellung von den Lösungen zu bekommen.

Wie stellt man ein ungleichheitsdiagramm dar?

Wie wir oben erwähnt haben, ist es nicht wirklich in Stein gemeißelt, aber die gebräuchlichste Methode besteht darin, den zugrunde liegenden Ausdruck der Ungleichung grafisch darzustellen und die x-Werte hervorzuheben, die die Ungleichung erfüllen. Dies ist möglicherweise das beste Grafikformat für diesen Zweck und wird von diesem Grafikprogramm verwendet.

Sie können auch ein eigenständiges Intervallobjekt zeichnen, aber das ist möglicherweise weniger aussagekräftig, da dadurch der Überblick darüber verloren geht, was tatsächlich mit der Ungleichung selbst geschieht.

Beispiel: ungleichungen grafisch darstellen

Stellen Sie die folgende Ungleichung grafisch dar: \(\frac{1}{x}+x > 1\)

Lösung: Wir erhalten die folgende Ungleichung, die gelöst werden muss:

\[\frac{1}{x}+x > 1\]

Wir müssen alle Begriffe der Ungleichheit auf eine Seite stellen:

\[x+\frac{1}{x}-1>0\]

Hilfsgleichung lösen

Aus obiger Ungleichung erhalten wir die zugehörige Gleichung, die zunächst gelöst werden muss:

\[x+\frac{1}{x}-1=0\]

Analyse der kritischen punkte

Wir müssen die gefundenen kritischen Punkte (aus den reellen Wurzeln des Zählers und Nenners) in aufsteigender Reihenfolge organisieren, Intervalle mit allen aufeinanderfolgenden kritischen Punkten definieren und das Vorzeichen der linken Größe der Ungleichung in jedem dieser Intervalle bewerten .

Der einzige kritische Punkt, der gefunden wurde, ist \(0\).

Auf dieser Grundlage müssen wir die folgenden Intervalle analysieren:

• Für das Intervall \(\left(-\infty, 0\right)\): Der Zähler ist positiv und der Nenner negativ, daher ist die linke Seite negativ, was bedeutet, dass \(\left(-\infty, 0\right)\) nicht Teil der Lösung ist.

• Für das Intervall \(\left(0, \infty\right)\): Der Zähler ist positiv und der Nenner ist positiv, also ist die linke Seite positiv, also ist \(\left(0, \infty\right)\) Teil der Lösung.

Lösung der ungleichheit

Ausgehend von der angegebenen Ungleichung und der Analyse der kritischen Punkte finden wir, dass die Lösung der Ungleichung lautet: \(x > 0\).

In Intervallschreibweise wird die Lösung wie folgt geschrieben:

\[\left(0,\infty\right)\]

Mit dem Ungleichheitsgraphen erhält man Folgendes:

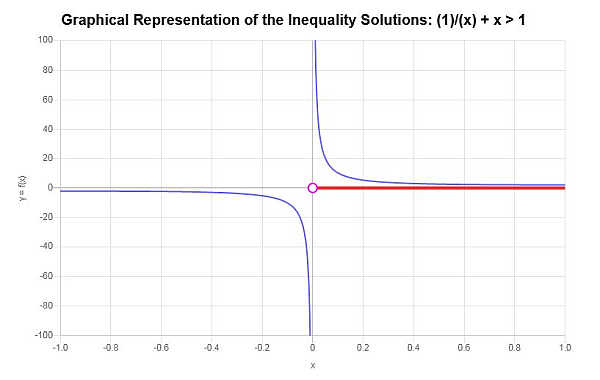
womit die Berechnung abgeschlossen ist.

Beispiel: polynomielle ungleichungen grafisch darstellen

Finden Sie den Graphen der Ungleichung: \(x^2 - 2x \ge 4\)

Lösung:

Wir müssen alle Begriffe der Ungleichheit auf eine Seite stellen:

\[x^2-2x-4\ge0\]

Hilfsgleichung lösen

Aus obiger Ungleichung erhalten wir die zugehörige Gleichung, die zunächst gelöst werden muss:

\[x^2-2x-4=0\]

Verwenden der quadratischen formel

Für eine quadratische Gleichung der Form \(a x^2 + bx + c = 0\) werden die Wurzeln mit Hilfe der folgenden Formel berechnet:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

In diesem Fall ist die Gleichung, die wir lösen müssen, \(\displaystyle x^2-2x-4 = 0\), was bedeutet, dass die entsprechenden Koeffizienten sind:

\[a = 1\] \[b = -2\] \[c = -4\]

Erstens werden wir die Diskriminanz berechnen, um die Art der Wurzeln zu bewerten.Die Diskriminierung wird berechnet als:

\[\Delta = b^2 - 4ac = \displaystyle \left( -2\right)^2 - 4 \cdot \left(1\right)\cdot \left(-4\right) = 20\]

Da die Diskriminante in diesem Fall \(\Delta = \displaystyle 20 > 0\) ist, die positiv ist, wissen wir, dass die Gleichung zwei verschiedene reelle Wurzeln hat.

Stecken Sie diese Werte nun in die Formel für die Wurzeln, die wir erhalten:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(1\right)\left(-4\right)}}{2\cdot 1} = \displaystyle \frac{2 \pm \sqrt{20}}{2}\]

Also finden wir das:

\[ {x}_1 = \frac{2}{2}-\frac{1}{2}\sqrt{20}=\frac{2}{2}-\sqrt{5}=1-\sqrt{5}=-\sqrt{5}+1 \] \[{x}_2 = \frac{2}{2}+\frac{1}{2}\sqrt{20}=\frac{2}{2}+\sqrt{5}=1+\sqrt{5}=\sqrt{5}+1\]

In diesem Fall hat die quadratische Gleichung \( \displaystyle x^2-2x-4 = 0 \) zwei reelle Wurzeln, also:

\[\displaystyle x^2-2x-4 = \left(x+\sqrt{5}-1\right)\left(x-\sqrt{5}-1\right)\]

das ursprüngliche Polynom wird also als \(\displaystyle p(x) = x^2-2x-4 = \left(x+\sqrt{5}-1\right)\left(x-\sqrt{5}-1\right) \) faktorisiert, womit die Faktorisierung abgeschlossen ist.

Analyse der kritischen punkte

Die Liste der gefundenen kritischen Punkte ist in aufsteigender Reihenfolge geordnet: \(-\sqrt{5}+1\), \(\sqrt{5}+1\).

Auf dieser Grundlage müssen wir die folgenden Intervalle analysieren:

- Für das Intervall \(\left(-\infty, -\sqrt{5}+1\right)\): Die linke Seite ist positiv, also ist \(\left(-\infty, -\sqrt{5}+1\right)\) Teil der Lösung.

- Für das Intervall \(\left(-\sqrt{5}+1, \sqrt{5}+1\right)\): Die linke Seite ist negativ, also ist \(\left(-\sqrt{5}+1, \sqrt{5}+1\right)\) nicht Teil der Lösung.

- Für das Intervall \(\left(\sqrt{5}+1, \infty\right)\): Die linke Seite ist positiv, was bedeutet, dass \(\left(\sqrt{5}+1, \infty\right)\) Teil der Lösung ist.

Lösung der ungleichheit

Ausgehend von der angegebenen Ungleichung und der Analyse der kritischen Punkte finden wir, dass die Lösung der Ungleichung lautet: \(x \le -\sqrt{5}+1\) oder \(x \ge \sqrt{5}+1\).

In Intervallschreibweise wird die Lösung wie folgt geschrieben:

\[\left(-\infty,-\sqrt{5}+1\right] \cup \left[\sqrt{5}+1,\infty\right)\]

Grafisch:

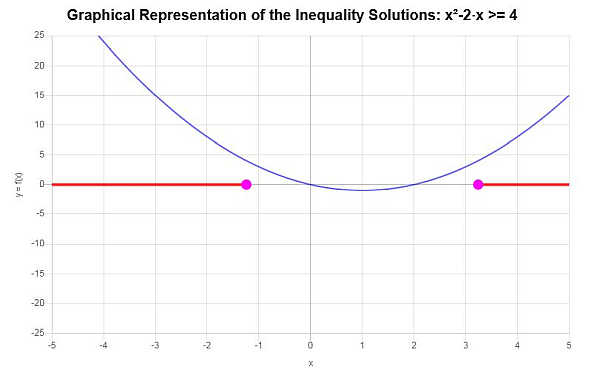
womit die Berechnung abgeschlossen ist.

Weitere algebra -taschenrechner

Während Sie beim Erlernen von Algebra und Infinitesimalrechnung vorankommen, wird Ihnen das wahrscheinlich langsam klar Lösen von Gleichungen eine entscheidende Rolle spielen. Und wenn Sie mehr lernen, wird Ihnen klar, dass wir manchmal weniger Informationen haben und am Ende vor dem Problem stehen Lösen von Ungleichungen .

Im Wesentlichen ist das Lösen von Ungleichungen nicht schwieriger als das Lösen von Gleichungen, es sind lediglich ein paar besser organisierte Schritte erforderlich. Das Hauptproblem besteht darin, dass wir die meisten Gleichungen nicht wirklich lösen können, zumindest nicht genau.

Und selbst wenn wir Gleichungen numerisch lösen, haben wir noch keine guten Möglichkeiten, um sicherzustellen, dass wir ALLE Lösungen für ALLE möglichen Gleichungen gefunden haben. Einige bemerkenswerte Gleichungen, die jederzeit gelöst werden können und in Anwendungen auftauchen, sind die Polynomgleichungen , das Sie mit den meisten Standardmethoden lösen können (jedoch nur für Polynome niedrigeren Grades)

Eine der am häufigsten gestellten Arten von Ungleichungen, die Sie in Ihren Mathematiktests lösen müssen, sind die rationalen Ungleichungen, da sie die schwierigste einfache Ungleichung sind, bei der Sie garantiert eine Lösung finden können (vorausgesetzt, die beteiligten Grade sind niedrig genug, oder). die Polynome sind einfach genug).