Rechner für inverse funktionen
Anweisungen: Verwenden Sie diesen Rechner, um die Umkehrfunktion für eine von Ihnen angegebene Funktion zu finden, wobei alle Schritte angezeigt werden. Bitte geben Sie den Funktionsausdruck, für den Sie die Umkehrfunktion finden möchten, in das Feld unten ein.
Mehr zu diesem inverse function calculator
Dieser Rechner ermöglicht es Ihnen, die Umkehrung einer gegebenen Funktion zu finden, indem er alle Schritte anzeigt, unter der Annahme, dass die Umkehrung existiert. Der Rechner untersucht die Funktion eine Gleichung lösen die mit der Definition der Funktion verknüpft ist, und versucht festzustellen, ob eine Umkehrung existiert oder nicht.
Sie können z. B. eine lineare Funktion wie "f(x) = 3x - 2" angeben, was ein einfacher Fall wäre, oder Sie könnten es mit einer etwas schwierigeren Funktion versuchen, z. B. mit einer rationalen Funktion wie "y = (x-1)/(x-3)".
Sobald Sie eine gültige Funktion eingegeben haben, klicken Sie bitte auf die Schaltfläche "Berechnen", um alle Schritte des Prozesses angezeigt zu bekommen, mit der Umkehrfunktion als endgültige Antwort, falls eine Umkehrfunktion existiert, oder mit der Erklärung, dass keine Lösung gefunden werden konnte und warum.
Es ist nicht garantiert, dass Sie alle inversen Funktionen finden werden. Erstens haben nicht alle Funktionen eine Umkehrfunktion, und zweitens (wie wir im nächsten Abschnitt sehen werden), beinhaltet der Prozess der Suche nach der Umkehrfunktion Lösung für x für eine Gleichung, und wie wir wissen, können einige Gleichungen sehr schwer oder unmöglich zu lösen sein.
Bei einfacheren Funktionen ist es also wahrscheinlicher, dass sich ihre Umkehrung finden lässt, falls diese existiert.

Wie definiert man den kehrwert einer funktion?
Laienhaft ausgedrückt, ist die Umkehrung einer Funktion die Funktion, die das Gegenteil von dem tut, was die ursprüngliche Funktion tut. Stellen Sie sich also eine Funktion in Form von y = f(x) vor, und dann können Sie sich vorstellen, dass Sie von x zu y gehen. Sie geben der Funktion ein x, und die Funktion gibt Ihnen ein bestimmtes y.
Die Umkehrfunktion geht von y aus und findet den Weg zurück zu x, und zwar so, dass das x dasselbe ist, das über die ursprüngliche Funktion zu y geführt hat. Die formale Definition erfolgt nun über funktionszusammensetzung . Für eine Funktion \(f\) sagen wir, dass \(g\) die Umkehrfunktion von \(f\) ist, wenn
\[ f(g(x)) = x \]und
\[ g(f(x)) = x \]für alle x in einer bestimmten Menge. Es gibt noch mehr, aber wir belassen es bei der intuitiven Ebene (Streng genommen muss eine Funktion injektiv und surjektiv sein, um invertierbar zu sein, und es gibt noch einige andere technische Aspekte, wie die Einschränkung der domäne und Bereich , usw.)
Normalerweise bezeichnen wir \(f^{-1}\) als den Kehrwert von \(f\), so dass die Formel, die den Kehrwert definiert, normalerweise wie folgt geschrieben wird:
\[ f(f^{-1}(x)) = x \]In welchen schritten wird die umkehrfunktion ermittelt?
- Schritt 1: Beginnen Sie mit der Gleichung, die die Funktion definiert, d. h. Sie beginnen mit y = f(x)
- Schritt 2: Je nachdem, wie komplex f(x) ist, kann es einfacher oder schwieriger sein, x zu lösen.
- Schritt 3: Unter bestimmten Umständen ist es einfach nicht möglich, für x zu lösen, z. B. bei komplexen nichtlinearen Funktionen f(x)
- Schritt 4: Wenn du in der Lage bist, für x zu lösen, dann solltest du in der Lage sein, x = g(y) zu schreiben
- Schritt 5: Sie müssen beurteilen, ob die gefundene Lösung eindeutig ist. Das heißt, ob die Lösung für x eindeutig ist. Mit anderen Worten: Haben Sie beim Lösen von x nur eine Lösung gefunden? Wenn ja, dann haben Sie eine inverse Funktion, andernfalls gibt es keine inverse Funktion
- Schritt 6: Wenn Sie die Umkehrung durch Lösen von x = g(y) gefunden haben, ändern Sie einfach den Namen der Variablen und schreiben f -1 (x) = g(x), was die Betonung darauf legt, dass g(x) die eigentliche Umkehrung ist
Wenn Sie Calculus und Ableitungen verwenden würden (aber beachten Sie, dass Sie KEINE Derivate um die Umkehrung zu berechnen), könnten Sie die Ableitung der Funktion finden und sicherstellen, dass die Ableitung immer positiv oder negativ ist, um sicherzustellen, dass die Funktion injektiv und somit invertierbar ist.
Aber in der Regel ist die Methodik der Lösung für x ist für Algebra-Grundschüler wesentlich angenehmer.
Die regel zum auffinden inverser funktionen
Es gibt eigentlich keine anderen Regeln für die Berechnung der Umkehrfunktion als die, dass man mit y = f(x) beginnt und dann nach x löst. Eine solche Regel klingt ziemlich allgemein, weil sie es auch ist. Sie ist mehr als eine Regel, sie ist eine allgemeine Methode für den Einstieg in den Prozess.
Letztlich hängt die Berechnung der Umkehrfunktion davon ab, ob es Ihnen gelingt, eine Gleichung zu lösen und sicherzustellen, dass diese Lösung eindeutig ist. Es ist hilfreich, den Graphen der Funktion im Voraus zu beurteilen, um nicht nach einer Umkehrung zu suchen, wenn es eindeutig keine gibt.
Worauf ist bei einem Graphen zu achten? Eine Funktion muss in einem bestimmten Teilbereich monoton (steigend oder fallend) sein, um invertierbar zu sein. Wir können den Bereich einer Funktion auf einen kleineren Teilbereich einschränken, um die Umkehrfunktion in einer kleineren Menge zu finden, was immer möglich ist.

Wie können wir sicher sein, dass die funktion eine inverse hat?
Die einzige Möglichkeit, um sicherzustellen, dass eine Funktion eine Umkehrfunktion hat, besteht darin, dass die Funktion injektiv (1 zu 1) ist. Dies wird entweder durch die Berechnung ihrer Ableitung (falls vorhanden) und die Sicherstellung, dass sie überall positiv und negativ ist, oder durch die manuelle Sicherstellung, dass wir immer eine eindeutige Lösung erhalten, wenn wir mit y = f(x) beginnen und nach x lösen.
Dies lässt sich auch grafisch veranschaulichen, indem man den Horizontallinientest verwendet: Man zeichnet eine beliebige horizontale Linie, und die Funktion f(x) besteht den Horizontaltest, wenn jede gezeichnete horizontale Linie den Graphen der Funktion höchstens einmal schneidet.

Beispiel: suche nach der umkehrfunktion
Finden Sie die Umkehrung der folgenden Funktion: \(f(x) = \displaystyle \frac{1}{3} x + \frac{5}{4}\)
Lösung:
Wir haben die folgende Funktion:
\[f(x) = \frac{1}{3} x + \frac{5}{4}\]Um die Umkehrung der gegebenen Funktion zu finden, müssen wir dann \(x\) lösen und feststellen, ob es eine Lösung gibt oder nicht. Die Ausgangsgleichung lautet:
\[y = \displaystyle \frac{1}{3}x+\frac{5}{4}\]Schritt 0: In diesem Fall müssen wir zunächst die gegebene lineare Gleichung vereinfachen, und dazu führen wir die folgenden Vereinfachungsschritte durch:
Lösen der linearen gleichung
Setzt man \(x\) auf die linke Seite und \(y\) und die Konstante auf die rechte Seite, erhält man
\[\displaystyle -\frac{1}{3}x = -y -\left(-\frac{5}{4}\right)\]Löst man nun \(x\), indem man beide Seiten der Gleichung durch \(-\frac{1}{3}\) dividiert, erhält man folgendes
\[\displaystyle x=-\frac{1}{-\frac{1}{3}}y+\frac{\frac{5}{4}}{-\frac{1}{3}}\]und vereinfachen wir endlich die folgenden
\[\displaystyle x=3y-\frac{15}{4}\]Daher führt die Lösung von \(y\) für die gegebene lineare Gleichung zu \(x=3y-\frac{15}{4}\).
Da wir bei der Lösung von \(x\) eine Lösung finden und es nur eine Lösung gibt, haben wir die Umkehrung gefunden.
Die inverse funktion
Auf der Grundlage der oben gezeigten Arbeit lässt sich schließen, dass die Umkehrfunktion lautet:
\[f^{-1}(x) = 3x-\frac{15}{4}\]Die Umkehrfunktion kann wie folgt grafisch dargestellt werden:
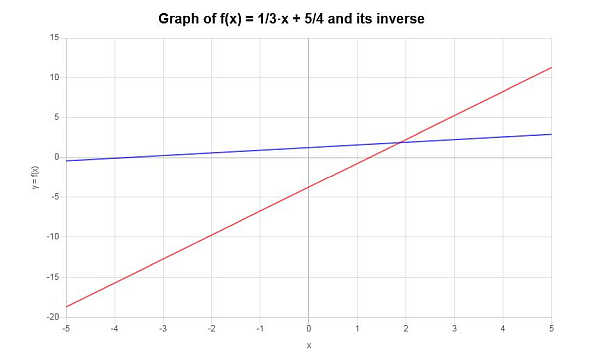
Beispiel: weitere inverse beispiele
Berechnen Sie die Umkehrfunktion von: \(y = \frac{x-1}{x+3}\)
Lösung:
Um die Umkehrung der gegebenen Funktion zu finden, lösen wir nach \(x\) und stellen fest, ob es eine Lösung gibt oder nicht. Die Ausgangsgleichung lautet:
\[y=\frac{x-1}{x+3}\]Es ergibt sich folgendes Bild:
Hilfszählergleichung
Wir müssen den Zähler gleich Null setzen und die Lösungen finden. Dann sind die Wurzeln, die den Nenner nicht gleich Null machen, Lösungen der rationalen Gleichung
Durch algebraische Manipulation der obigen Polynomgleichung ergibt sich folgendes:
\[x = -\frac{3y+1}{y-1} \]Hilfsnennergleichung
Wir finden die Wurzeln des Nenners: \(x+3=0\)
Daher führt die Lösung von \(x\) für die gegebene lineare Gleichung zu \(x=-3\).
Zusammensetzen der lösungen der rationalen gleichung
Wenn wir dann überprüfen, dass wir keine Null im Nenner haben, finden wir die folgende Lösungsmenge der Gleichung \(\displaystyle y=\frac{x-1}{x+3}\)
\[x = -\frac{3y+1}{y-1} \]Da wir bei der Lösung von \(x\) nur eine einzige Lösung finden, können wir davon ausgehen, dass wir eine Umkehrfunktion haben.
Ermittlung der inversen funktion
Auf der Grundlage der oben gezeigten Arbeit lässt sich schließen, dass die Umkehrfunktion lautet:
\[f^{-1}(x) = -\frac{3x+1}{x-1}\]Die gefundene Umkehrfunktion kann wie folgt grafisch dargestellt werden:
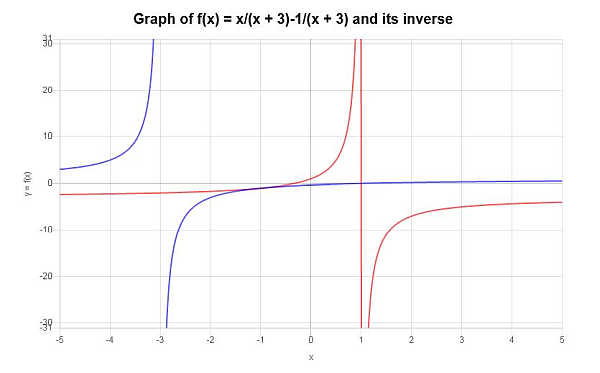
Beispiel: nicht alle funktionen sind invers
Hat die folgende Funktion eine Umkehrfunktion? \( y = \displaystyle \frac{1}{3} x^2 - \frac{2}{5} \) ?
Lösung: Beachten Sie, dass
\[ y =\displaystyle \frac{1}{3} x^2 - \frac{2}{5} \] \[ \displaystyle \Rightarrow y + \frac{2}{5} = \frac{1}{3} x^2 \] \[ \displaystyle\Rightarrow x^2 = 3\left(y + \frac{2}{5} \right) \] \[\displaystyle \Rightarrow x = \pm \sqrt{ 3\left(y + \frac{2}{5} \right) }\]was bedeutet, dass es zwei Lösungen gibt, und dass es in diesem Fall keine Umkehrung gibt.
Weitere funktionsrechner
Funktionen sind ein wichtiger Gegenstand in der Mathematik, insbesondere in der Infinitesimalrechnung und der Algebra, wo viele Verbindungen zwischen Variablen über Funktionen hergestellt werden.
Es gibt viele Möglichkeiten, die Funktion zu nutzen: Sie können sie zu vereinfachen , du kannst eine Funktion differenzieren sie können sie bedienen, das Kompositum mit einer anderen Funktion finden und die Liste lässt sich beliebig fortsetzen.
Selbst wenn Sie Funktionen explizit erwähnen, haben Sie oft Funktionen, die dem gesamten Prozess zugrunde liegen. Sie sind also vorhanden, auch wenn man es manchmal nicht weiß. Eine tolle Sache ist, dass man selbst bei sehr komplizierten Funktionen immer Grafik eine Funktion um sich ein Bild von ihrem Verhalten zu machen, also zumindest eine Vorstellung davon zu bekommen, was die Funktion tut (geht hoch, geht runter usw.).




