Domäne und Reichweite
Die Domäne einer Funktion ist eine Menge, in der eine Funktion gut definiert ist. Insbesondere sei \(f: D \rightarrow R\) eine Funktion, was bedeutet, dass \(f(a)\) für \(a \in D\) gut definiert ist. Die Domäne der Funktion \(f\) ist die Menge \(D\).
Mathematisch schreiben Sie \(dom(f) = D\).
Der Bereich einer Funktion ist dagegen eine Reihe von Werten, die über die Funktion erreicht werden können.
Insbesondere sei \(f: D \rightarrow R\) eine Funktion, der Bereich ist die Menge aller möglichen Werte \(b \in R\), für die \(a \in D\) existiert, so dass \(f(a) = b\).
Oft wird der Bereich einer Funktion als \(R(f)\) oder auch als \(f(D)\) geschrieben (was über die Funktion \(f\) auch als Bildsatz von \(D\) bezeichnet wird).
Es ist wichtig, die Domäne einer Funktion zu kennen, da dies uns einen sicheren Satz von Werten gibt, für die die Funktion genau definiert ist.
Dann ist der Bereich wichtig, weil er uns sagt, welche Werte von der Funktion erreicht werden. Eine grafischere Interpretation lautet wie folgt: Ein Punkt \(b\) liegt im Bereich von \(f\), wenn die horizontale Linie \(y = b\) den Graphen der Funktion \(f(x)\) schneidet.
Wie berechnet man die Domain in der Praxis?
Hier erfahren Sie, wie Sie Domain und Reichweite finden ::
Für die Domäne müssen Sie zuerst die Punkte finden, an denen die Funktion NICHT definiert ist. Die Quellen für undefinierte Operationen sind die Division durch Null oder die Quadratwurzel einer negativen Zahl.
Sie müssen also die Punkte (falls vorhanden) finden, an denen diese undefinierten Operationen auftreten. Und die Domäne wird der Rest der Punkte sein, dh alle Punkte mit Ausnahme derjenigen, die Sie finden und die undefinierte Operationen verursachen.
Wie berechnet man den Bereich in der Praxis?
Sei \(y\) eine Zahl und wir lösen für \(x\) die folgende Gleichung \(f(x) = y\). Der Wert \(y\) liegt im Bereich, wenn \(f(x) = y\) für \(x\) gelöst werden kann.
Das ist also etwas kniffliger: Sie müssen herausfinden, ob Sie \(y\) in irgendeiner Weise einschränken müssen, damit \(f(x) = y\) eine Lösung für \(x\) hat.
BEISPIEL 1
Berechnen Sie die Domäne und den Bereich der Funktion \(\displaystyle f(x) = \frac{x+1}{x-1}\).
ANTWORTEN:
Bedenken müssen wir die Domain bezahlen. Wir müssen sehen, wo die Funktion gut ist ist. Wenn es sich darum handelt, dort zu beginnen, wo es nicht genau ist.
In diesem Herbst werden alle Arbeitskräfte zu seinem, bis zu einem: Der Nenner kann nicht Null sein.
Anmerkung: Der Hauptschlüssel zum Auffinden der Domäne gehört dazu, die Punkte zu verlieren, ein zu verlieren, zu verlieren, zu verlieren und zu verlieren.
Daher ist die Funktion AUSSER bei \(x-1 = 0\) gut beeinflusst, war bei \(x = 1\) Daher sagen wir, dass die Domäne die gesamte reelle Linie mit Ausnahme des Werts \(1\) ist.
Unter Verwendung der Intervallnotation versucht wir \(dom(f) = (-\infty, 1) \cup (1, +\infty)\) schreiben.
Jetzt müssen wir den Bereich beziehen. Der Verlust ist es etwas müdesamer, die Reichweite zu verlieren, als die Domain zu gehört, aber jetzt geht es los.
Es gibt viele Möglichkeiten, den Bereich zu gehören: Einige gehört sich zu der grafischen Darstellung der Funktion, um einen Anspruch auf den Bereich einer Funktion zu gehört. Das heißt, dass es keine echte Antwort gibt, nur eine gebildete Vermutung.
Der andere Weg ist der formale mathematische Weg: Sei \(y\) eine Zahl und wir werden für \(x\) die richtigen Beziehungen \(f(x) = y\) geholfen. Der Wert \(y\) liegt im Bereich, wenn \(f(x) = y\) für \(x\) wird werden kann.
In diesem Herbst haben wir:
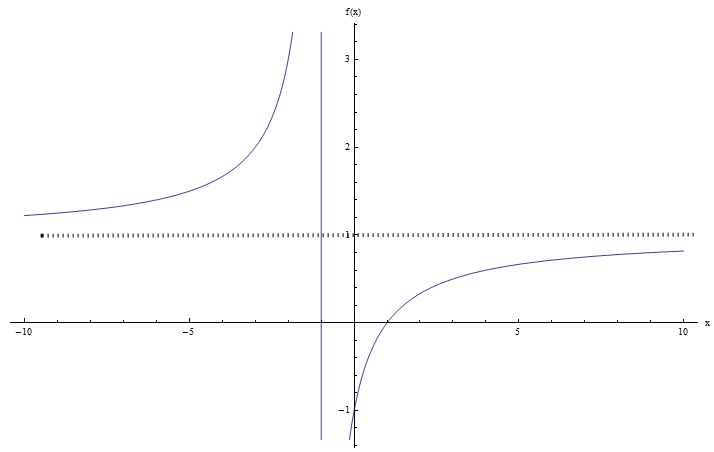
\[\large f(x) = y \Leftrightarrow \frac{x+1}{x-1} = y\] \[\Rightarrow \,\,\,x+1=y\left( x-1 \right)\] \[\Rightarrow \,\,\,x+1=yx-y\] \[\Rightarrow \,\,\,x-yx=-1-y\] \[\Rightarrow \,\,\,x\left( 1-y \right)=-1-y\] \[\Rightarrow \,\,\,x=\frac{y+1}{y-1}\]Wann ist \(x\) gut beeinflusst? Fast für alle \(y\), außer wenn \(y = 1\), weil wir in diesem Fall eine Division durch \(0\) haben. Daher ist der Bereich von \(f\) in diesem Herbst die gesamte reelle Linie mit Ausnahme von 1.
Unter Verwendung der Intervallnotation versucht wir \(R(f) = (-\infty, 1) \cup (1, +\infty)\) schreiben.
BEISPIEL 2
Berechnen Sie die Domäne und den Bereich der Funktion \(\displaystyle f(x) = \sqrt{x+1}\).
ANTWORTEN:
In diesem Herbst gibt es keine Divisionen, aber wir müssen keine, dass \(x+1\ge 0\), damit es keine Quadratwurzeln gibt von negativen Werten. Dann brauchen wir wir wir \(x \ge -1\).
.Für den Bereich müssen wir nun nach \(x\): \(\sqrt{x+1} = y\) auffolgen. Die Quadratwurzel von etwas ist gleich negativ, auch gebraucht wir führen das \(y \ge 0\).
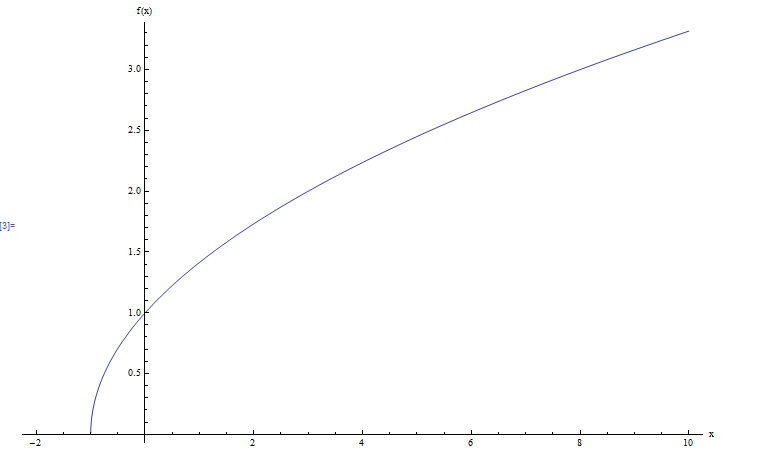
Wenn Sie auf beide Seiten ein Quadrat erhalten, erhalten Sie \(x+1 = y^2\). Die Lösung gehört auch \(x = y^2-1\). Die Rechte Rechte, die wir \(y\) auferlegen müssen, ist die von \(y \ge 0\). Daher schreiben wir unter unter der Intervallnotation \(R(f) = [0, +\infty)\) schreiben. Grafisch:
Weitere Informationen zu Domain und Bereich
Lassen Sie uns auch als Zusammenfassung einige Dinge zusammenfassen. Es ist in der Domäne eine Funktion genau gegeben, und der Bereich ist die Menge der Punkte, die durch die Funktion geworden sind.
In Bezug auf die Beschränkung ist es sich darum, die Domäne zu finden, als den Bereich zu finden. Betroffene versuchen, einige Leute, den Bereich grafisch zu finden, aber das ist, dass weniger genau. Grafische Antworten müssen mit Vorsicht behandelt werden.
Sie können Tutorials lesen über lesen wie man die Domain findet und die Reichweite , die sich selbst auf jeden Fall gehört wird.
