Funktionsgrafik

Mit diesem Funktionsgraphenrechner können Sie den Graph jeder von Ihnen bereitgestellten Funktion generieren.Sie müssen eine gültige Funktion in x bereitstellen.

Es könnte eine Funktion sein, die bereits vereinfacht ist, wie f (x) = sin (2x), oder es könnte etwas komplexer sein wie 'f (x) = sin ((1/3 x +1/4 x^2)(1/5 x +1/6)) ', und dieser Taschenrechner macht das Funkionsver EinfacherLangung für dich.

Sobald Sie eine gültige Funktion in das entsprechende Formular eingegeben haben, müssen Sie nur auf "Berechnen" klicken, um das generierte Diagramm zu erhalten.

Arbeiten mit dem Grafik Einer Funkion Kann Ihnen helfen, die Haupteigenschaften zu verstehen.In der Tat das Funksgrafik Kann Ihnen letztendlich alles, was Sie über das Verhalten der Funktion brauchen, sagen: Steigt sie?Nimmt es ab?Überquert es die X-Achse?Hat es irgendeine Art von Symmetrie?

Was ist die funktionsgrafik?

Das Funktionsgraphen für eine gegebene Funktion f (x) ist der Satz von Punkten (x, f (x)).Wenn dies in den X-Y-Achsen gezeichnet ist, sieht es aus wie eine "Kurve" (könnte eine Linie sein), die von links nach rechts fließt.

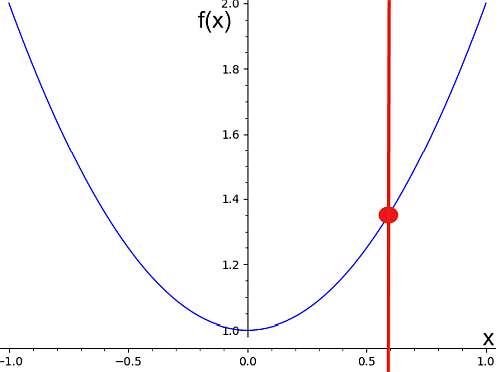
Nun hat dieser Strömungen von links nach rechts eine sehr spezifische Eigenschaft: Es besteht den vertikalen Linientest, der darauf hinweist, dass der Diagramm einer Funktion, wenn sie sich mit einer vertikalen Linie überschneidet, höchstens einen Schnittpunkt aufweist.Beispielsweise entspricht das folgende Diagramm einem Funktionsgraphen, da es den vertikalen Linientest übergeht.

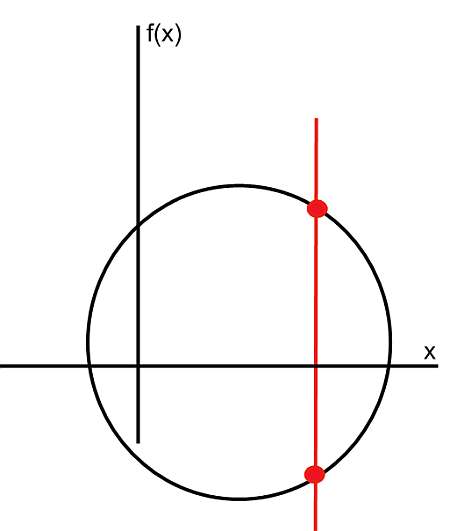
Andererseits entspricht die folgende Grafik nicht dem Graphen einer Funktion, da wir eine vertikale Linie sehen können, die die Kurve an zwei Punkten überschreitet.

Was sind die schritte zum finden des funktionsgraphen?

• Schritt 1: Identifizieren Sie die Funktion, die Sie drapieren möchten.Bewerten Sie durch Inspektion, ob die Funktion gültig ist oder nicht
• Schritt 2: Wenn die Funktion ein gültiger Ausdruck ist, finden Sie potenzielle Punkte, an denen die Funktion nicht bewertet werden kann (Abteilungen nach Null- oder Quadratwurzeln negativer Zahlen).
• Schritt 3: Vereinfachen Sie so viel wie möglich Setzzendsi
• Schritt 4: Versuchen Sie, bekannte Muster zu identifizieren.Ist die Funktion in ihrer einfachsten Form ein Polynom?Polynome haben eine bestimmte Form.Ist die Funktion eine trigonometrische Funktion?Sie haben auch eine sehr bekannte und charakteristische Form
• Schritt 5: Wenn Sie kein einfaches, erkennbares Muster oder bekannter Funktion haben, erstellen Sie eine Tabelle mit Punkten (x, f (x)), so viele Punkte wie es praktisch ist
• Schritt 6: Zeichnen Sie diese Punkte aus Ihrer Tabelle auf der XY -Ebene.Verfolgen Sie eine Kurve durch diese Punkte, um ein Gefühl dafür zu bekommen, wie das Funktionsgrafik aussieht

Vereinfachung der Funktion In der einfachsten Form können Sie auf einfachere Art und Weise identifizieren, die bekannte Funktionen erscheint und leicht grafisch dargestellt werden können.

Wie grafikiere ich bekannte funktionen?

Wann Vereinfachung Einer Funkion Erwarten Sie nicht, dass Sie direkt sehr einfache Dinge wie \(f(x) = x^2\) (eine einfache Parabola) oder \(f(x) = x\) (eine einfache Zeile) haben, aber Sie haben möglicherweise Übersetzungen von skalierten Versionen dieser grundlegenden.In der Tat zum Beispiel alle Quadratische Funkion kann in Scheitelpunktform Sie hilft Ihnen dabei, die Kurve als einfache Parabel zu identifizieren, die übersetzt wird.

Was sind die schritte zum durchführen von funktionsgraphentransformationen?

• Schritt 1: Identifizieren Sie die Funktion, die Sie drapieren möchten
• Schritt 2: Vereinfachen Sie so viel wie möglich, wie Sie die Falle von vermeiden können Durchnull Teilen und quadratische Wurzel negativer Werte nehmen
• Schritt 3: Mit der einfachsten Version der Funktion sehen Sie, ob elementare Funktionen erkannt werden können
• Schritt 4: Wenn nicht, prüfen Sie, ob eine Transformation gemeinsamer Funktionen (Polynome, Linien, Linien, Triggfunktionen kann identifiziert werden, da diese auch leicht zu grafisch sind
• Schritt 5: Wenn alles oben fehlschlägt, konstruieren Sie einfach eine Tabelle mit Werten (x, f (x)) und verfolgen Sie die Form der Grafik manuell

Natürlich müssen Sie es nicht manuell ein gratschen, Sie können dies verwenden FunkionsDiagramm Online Werkzeug, um ein genaues und ordentlich aussehendes Diagramm zu erhalten.

Warum möchten sie über funktionsgraphentypen wissen?

Die Grafik einer Funktion kann Ihnen im Wesentlichen alles über die Funktion erzählen.Bis zu einem bestimmten Punkt ist das Diagramm der Funktion das Funkwerk , oder zumindest eine Darstellung davon.

Es gibt eine Korrespondenz zwischen Funktion und Grafik, die darauf hinweist, dass der Diagramm Ihnen im Wesentlichen alles sagt, was Sie über die Funktion wissen müssen.

Beispiel: finden der funktionsgrafik

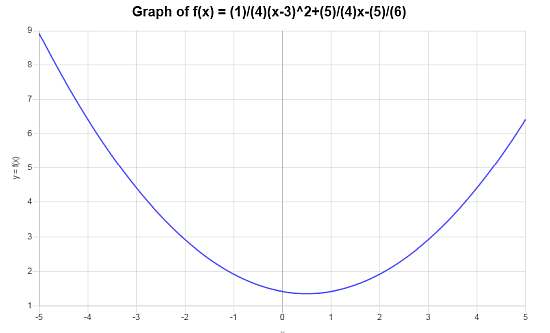
Berechnen Sie den Funktionsgraphen der folgenden: \(f(x) = \frac{1}{4}(x-3)^2 + \frac{5}{4} x - \frac{5}{6}\)

Lösung: Die folgende Funktion wurde \(\displaystyle f(x) = \frac{1}{4}\left(x-3\right)^2+\frac{5}{4}x-\frac{5}{6}\) bereitgestellt, für die wir sein Diagramm konstruieren müssen.

Schritt 0: In diesem Fall müssen wir zunächst die angegebene Funktion \(\displaystyle f(x) = \frac{1}{4}\left(x-3\right)^2+\frac{5}{4}x-\frac{5}{6} \) vereinfachen, und dazu führen wir die folgenden Vereinfachungsschritte durch:

Das folgende Diagramm wird für die vereinfachte Funktion \(\displaystyle f(x)=\frac{1}{4}x^2-\frac{1}{4}x+\frac{17}{12}\) im Intervall \([-5, 5]\) erhalten:

Beispiel: funktionsgrafikregeln

Berechnen Sie das Diagramm für die Funktion \(f(x) = \frac{1}{3}(x-4)^2 - \frac{5}{6}\).Ist diese Funktion eine Funktionsgrafiktransformation einer grundlegenden, bekannten Funktion?

Lösung: Erweitern und Vereinfachung der Funktion:

Das folgende Diagramm wird für \(\displaystyle f(x)=\frac{1}{3}x^2-\frac{8}{3}x+\frac{9}{2}\) im Intervall \([-10, 10]\) erhalten:

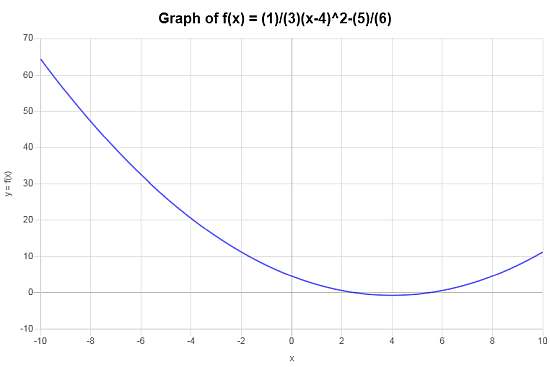
In diesem Fall ist die Grafik \(f(x) = \frac{1}{3}(x-4)^2 - \frac{5}{6}\) in der Tat die Transformation des einfachen \(g(x) = x^2\), das von 4 Einheiten verletzt wurde, von \(\frac{5}{6}\) und neu skaliert wurde.

Beispiel: ein weiteres funktionsgrafikbeispiel

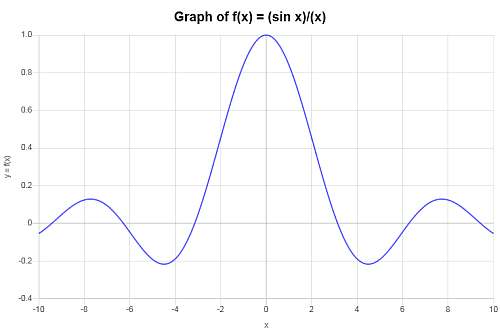
Berechnen Sie den Diagramm von \( f(x) = \displaystyle \frac{\sin(x)}{x}\).

Lösung: Die folgende Funktion wurde bereitgestellt: \(\displaystyle f(x) = \frac{\sin\left(x\right)}{x}\), daher wird das folgende Diagramm erhalten, Intervall \([-10, 10]\):

Andere funktionsrechner

Bei einer Funktion möchten Sie dazu in der Lage sein Vereinfachen Sie Die Fungion , um es in seine einfachste Form zu bringen.Wir haben bereits gesehen, dass dies von Vorteil ist, um die potenzielle Funktionsgrafiktransformation aus grundlegenden Funktionen, die dort sein können, einfacher zu identifizieren.