Mehr über trig -derivate

Verwenden Sie diesen Taschenrechner, um trigonometrische Derivate zu finden, die in diesem Fall eine gültige differenzierbare Funktion annehmen, die eine oder mehrere elementare TRIG -Funktionen beinhaltet.

Ein Beispiel für eine gültige Funktion für diesen Taschenrechner ist f (x) = sin (x)/x oder f (x) = x*sin (x^3), nur um ein Beispiel zu geben.

Wenn Sie die entsprechende Funktion bereits eingegeben haben, können Sie dann auf die Schaltfläche "Berechnen" klicken, um alle Schritte der Berechnung des Ihnen gezeigten Ableitung zu erhalten.

Trigonometrische Funktionen spielen auch eine entscheidende Rolle bei der Kalkül, in Berechnung von Derivaten Im Algemeinen.Letztendlich können komplexere Funktionen ihre Derivate auf die Berechnung des Derivats für einfachere Trigmfunktionen reduzieren.

Grundlegende trig -derivate

Die Idee, Ableitungsregeln zu verwenden, besteht darin, eine komplexe Funktion zu brechen und sie unter Verwendung der Derivate bekannter Funktionen zu unterscheiden.Insbesondere einfache Trigmfunktionen wie Sinus, Cosinus, Tangente und Kotangent spielen dabei eine wichtige Rolle.

Was sind die grundlegenden trig -derivate?

• Trigend Derivat 1: \(\frac{d}{dx} \sin (x) = \cos(x)\)
• Trigend Derivat 2: \(\frac{d}{dx} \cos (x) = -\sin(x)\)
• Trigend Derivat 3: \(\frac{d}{dx} \tan (x) = \sec^2(x)\)
• Trigend Derivat 4: \(\frac{d}{dx} \cot (x) = -\csc^2(x)\)
• Trigend Derivat 5: \(\frac{d}{dx} \sec (x) = \sec(x)\tan(x)\)
• Trigend Derivat 6: \(\frac{d}{dx} \sec (x) = -\csc(x)\cot(x)\)

Dies sind die grundlegenden Derivate, die Sie sehr wissen und möglicherweise auswendig lernen müssen, um sie zu verwenden Fähigkeitsregeln um kompliziertere Derivate zu berechnen

Sind trig -derivate in grad?

Nein, die Ableitung von Triggfunktionen ist in Radians Daher spiegeln die festgestellten Trig -Derivate die Tatsache wider, dass das Argument X in Radians gemessen wird.

Nehmen wir also zum Beispiel an, dass wir das Derivat der Sünde in der Sünde berechnen wollten Grad Also definieren wir \(f(y) = \sin(y)\), wobei \(y\) in Grad gemessen wird.

Lassen Sie nun \(x = \frac{\pi y}{180}\) der äquivalente Winkel in Radians sein und auch für \(y\) wir finden, dass \(y = \frac{180 x}{\pi}\) dann die Kettenregel verwenden:

\[\displaystyle \frac{d}{dy} f(y) = \displaystyle \frac{d}{dy} f(y(x)) \frac{dy}{dx} = \frac{180}{\pi} \cos(y) \]

Basierend darauf ist das Ableitung von Sinus in Grad tatsächlich Cosinus in Grad, aber ein Faktor \(\frac{180}{\pi}\).

Wie finden sie derivate in der trigonometrie?

Trig -Derivate werden per Definition unter Verwendung grundlegender Trig -Identitäten gefunden.Zum Beispiel die Verwendung der Sinus der Summenformel Wir können die Ableitung von \(\sin(x)\) unter Verwendung der Definition der Grenze ableiten:

\[\displaystyle \frac{d}{dx} \sin(x) = \displaystyle \lim_{h \to 0} \frac{\sin(x+h)-\sin(x)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)\cos(h) + \cos(x)\sin(h) - \sin(x)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)(\cos(h)-1) + \cos(x)\sin(h)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} + \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} \right)+ \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \sin(x) \displaystyle \lim_{h \to 0} \left( \frac{(\cos(h)-1)}{h} \right)+ \cos(x) \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \sin(x) \cdot 0 + \cos(x) \cdot 1 = \cos(x)\]

Tipps und tricks

Die wichtigsten Erkenntnisse für Sie sind es, immer daran zu erinnern, was die 6 trigg -dederes Sinx und kennen sie auswendig, wie Sie sie kontinuierlich zusammen mit dem Basic benutzen werden Differenzierung von Regeln .

In ähnlicher Weise können Sie Trig -Identitäten und die Definition der inversen Funktion verwenden, um die häufigsten inversen Trig -Derivate zu finden.

Beispiel: berechnung der trigend derivat

Betrachten Sie die folgende Funktion: \(f(x) = \sin^2(x)+ \frac{1}{x}\).Finden Sie seinen Derivat

Lösung: Trig -Derivate beinhalten die Trig -Funktion, die differenziert werden müssen.Betrachten Sie die Funktion \(\displaystyle f(x)=\sin\left(x\right)^2+\frac{1}{x}\), die eine Sinusfunktion enthält, sodass sie als Trig -Derivat qualifiziert ist.

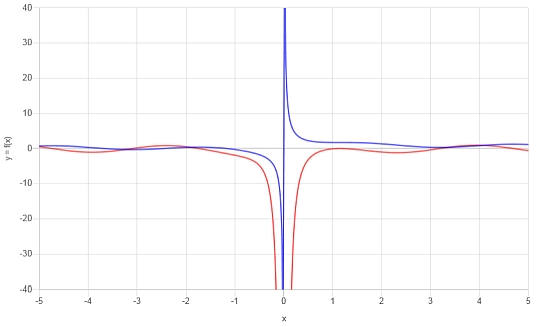
Ergebnisse : Für dieses Beispiel wird festgestellt, dass das Derivat lautet:

\[f'(x) = \frac{2x^2\cos\left(x\right)\sin\left(x\right)-1}{x^2}\]

Es ist sehr nützlich, die Funktion und ihre Ableitung in einem Diagramm darzustellen.Siehe unten:

Beispiel die ableitung einer trig -funktion

Betrachten Sie die folgende TRIG -Funktion: \(f(x) = \sin(x) + x \cos(x)\), finden Sie ihre Ableitung.

Lösung: Jetzt müssen wir mit der Ableitung der folgenden Trig -Funktion \(\displaystyle f(x)=\sin\left(x\right)+x\cos\left(x\right)\) arbeiten.

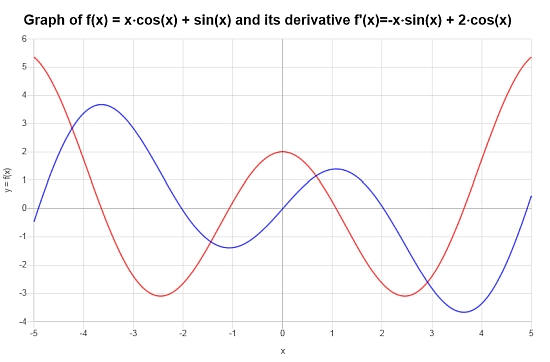
Schlußfolgerung : Wir schließen daraus, dass das Derivat gegeben wird durch:

\[f'(x) = -x\sin\left(x\right)+2\cos\left(x\right)\]

Das folgende Diagramm wird erhalten:

Beispiel: trig -derivate und implizite differenzierung

Finden Sie \(\frac{dy}{dx}\) für \( \sin(x)+\cos(y) = 1 \).

Lösung: Wir müssen verwenden Implizit -Unterschied Also unterscheiden wir beide Seiten und verwenden die Kettenregel :

\[ \frac{dy}{dx}\left(\sin(x)+\cos(y)\right) = \frac{dy}{dx} \left(1\right) \] \[\Rightarrow \cos(x)-\sin(y)y' = 0 \] \[\Rightarrow \sin(y)y' = \cos(x) \] \[\Rightarrow y' = \frac{\cos(x)}{\sin(y)} \]

was die Berechnung abschließt.

Andere nützliche derivatrechner

Funden des Derivats von einfachen und elementaren Funktionen ist der Eckpfeiler des Prozesses, die Derivate von komplizierteren Funktionen zu finden, indem sie die bekannten Verwendung verwenden Differenzierungsregeln .

In diesem Zusammenhang grundlegend Trigonometrische Funktionen Kann als Elementarfunktionen angesehen werden, für die das Derivat über seine Definition unter Verwendung von Grenzen berechnet werden kann.Zu den nützlichsten elementaren Funktionen, die wir haben Polynom und rationale Funktionen.