Horizontaler linientest

Mit diesem Rechner können Sie den horizontalen Linientest für jede beliebige Funktion durchführen, die Sie angeben, und dabei die Schritte anzeigen. Die von Ihnen angegebene Funktion könnte z. B. "y = 2x - 1" sein, was die einfachste Art von lineare Funktion finden können, oder Sie können eine komplexere Funktion wie "y = (2x-1)/(x+1)" angeben, die eine rationale Funktion .

Sobald Sie eine gültige Funktion eingegeben haben, können Sie auf die Schaltfläche "Berechnen" klicken. Daraufhin werden Ihnen alle Schritte des Prozesses angezeigt und Sie erfahren, ob die Funktion den Horizontallinientest (HLT) besteht oder nicht.

Die Funktionsweise dieses Rechners besteht darin, dass er eine allgemeine horizontale Linie festlegt und prüft, wie oft (wenn überhaupt) die Linie diese beliebige horizontale Linie kreuzt. Dies beinhaltet Lösung für x die Gleichung y = f(x).

Was ist der horizontale linientest?

Der HLT ist ein Test, mit dem Sie feststellen können, ob eine Funktion eineindeutig ist oder nicht. Er besteht darin, horizontale Linien in verschiedenen Höhen zu zeichnen und zu sehen, wo sie den Graphen der gegebenen Funktion f(x) schneiden, wenn sie es überhaupt tun.

Wenn keine horizontale Linie, die Sie sich vorstellen können, den Graphen der Funktion f(x) mehr als einmal schneidet, dann die Funktion ist eineindeutig . Wenn Sie hingegen eine horizontale Linie finden können, die den Graphen der Funktion f(x) MEHR ALS EINMAL schneidet, dann haben Sie bewiesen, dass die Funktion NICHT eineindeutig ist

Jetzt werden Sie vielleicht denken: "Moment mal", dieses Tool funktioniert nicht wirklich, um zu beweisen, dass eine Funktion eins-zu-eins ist, sondern um zu beweisen, dass sie NICHT eins-zu-eins ist, indem man den horizontalen Linientest verwendet.

Denn in der Praxis kann ich unmöglich ALLE horizontalen Linien grafisch darstellen, um zu prüfen, wie oft sie den Graphen von f(x) kreuzen, aber wenn ich EINE horizontale Linie finde, die den Graphen von f(x) zu oft kreuzt, dann weiß ich, dass es nicht eins zu eins ist. Also, gute Idee, du bist da auf einer guten Spur.

Anwendung des tests der horizontalen linie in der praxis

Wenn Sie z. B. die Funktion \(f(x) = x^2\) haben, würde das Diagramm in etwa so aussehen:

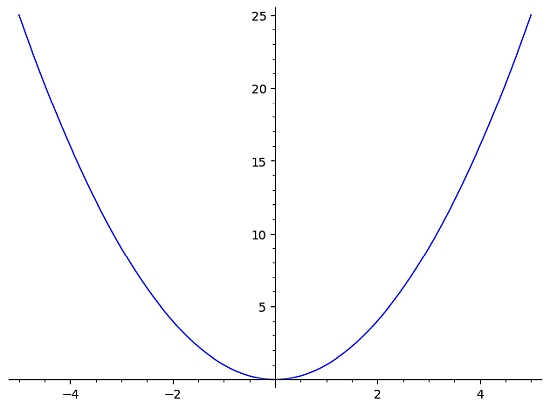
In diesem Fall sehen wir sofort, dass diese Funktion den Horizontallinientest nicht besteht. Der Grund dafür ist, dass die horizontale Linie y = 10, die im folgenden Diagramm dargestellt ist, den Graphen von f(x) zweimal (mehr als einmal) schneidet

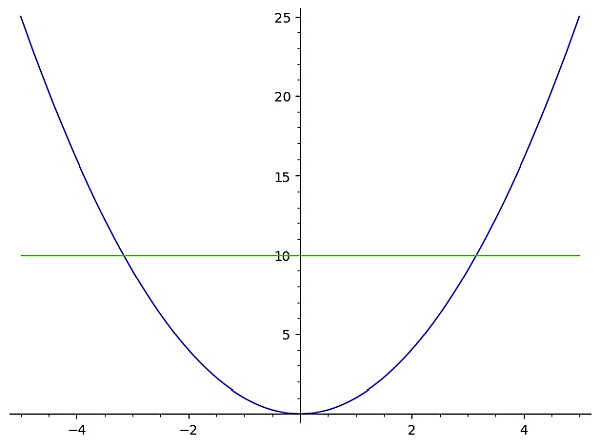
In diesem Fall besteht die Funktion \(f(x) = x^2\) den Test auf eine horizontale Linie nicht und ist daher keine eins-zu-Eins-Funktion .

Da es unmöglich ist, ALLE möglichen horizontalen Linien zu testen, muss der HLT mit algebraischen Mitteln versucht werden, es sei denn, Sie sehen visuell einen klaren Fall einer horizontalen Linie, der die Funktion den Test nicht bestehen lässt.

Verwendung des horizontal linientests (analytisch)

• Schritt 1: Ausgehend von einer gegebenen gültigen Funktion f(x) setzen Sie die Höhe einer horizontalen Linie auf einen beliebigen Wert von y
• Schritt 2: Sie stellen also die Gleichung auf: y = f(x), und das Ziel ist es, x zu lösen
• Schritt 3: Es gibt nicht die eine Strategie, um diese Gleichung lösen sie hängt von der Art der Funktion f(x) ab. Wenn f(x) eine einfache lineare oder quadratische Funktion ist, dann ist es recht einfach, x zu lösen. Wenn nicht, dann müssen verschiedene Methoden getestet werden
• Schritt 4: Wenn beim Lösen von x mehr als eine Lösung für ein beliebiges y gefunden wird, dann besteht die Funktion den HLT nicht. Andernfalls, wenn es nur eine Lösung oder keine Lösung gibt, besteht sie die Prüfung.

Das Subtrahieren von Fraktionen wird nur durch die Summe der Brüche abgeleitet: Um zwei Fraktionen zu subtrahieren, multiplizieren Sie nur den zweiten mit -1 und fügen Sie es dem ersten hinzu .

Kann die horizontale linie negative oder positive werte annehmen?

Das Wichtigste an der analytischen Umsetzung der HLT ist, dass Sie eine beliebige horizontale Linie wählen. Es kann ein beliebiger Wert sein, entweder positiv oder negativ. Der willkürlich gewählte Wert von y KANN dann bestimmen, ob die vorgeschlagenen Lösungen gut definiert sind oder nicht, aber er fügt nicht mehr Lösungen hinzu, sondern kann stattdessen Lösungen subtrahieren.

Wenn Sie zum Beispiel mit \(f(x)= \frac{2x+1}{x-1}\) beginnen und x wie folgt lösen: \(y = \frac{2x+1}{x-1}\), so erhält man

\(x = \frac{y+1}{y-2}\)

was bedeutet, dass es für ein gegebenes \(y\) MINDESTENS eine Lösung gibt. Warum höchstens eine Lösung? Weil es für y = 2 eigentlich keine Lösung gibt, und für jedes andere y gibt es eine Lösung. Dies eignet sich hervorragend, um zu zeigen, dass die Funktion den Test der horizontalen Linie besteht.

Beispiel: bestehen des hlt

Besteht die folgende Funktion den HLT: \(f(x) = \frac{1}{3} x + \frac{5}{4}\) ?

Lösung:

Die bereitgestellte Funktion ist:

\[f\left(x\right) = \frac13x+\frac54\]

Um festzustellen, ob die gegebene Funktion den Horizontalen Linientest besteht oder nicht, müssen wir \(x\) lösen und feststellen, ob es keine Lösung, eine Lösung oder mehrere Lösungen gibt. Die Ausgangsgleichung lautet

\[y=\frac{1}{3}x+\frac{5}{4}\]

Lösen der linearen gleichung

Setzt man \(x\) auf die linke Seite und \(y\) und die Konstante auf die rechte Seite, erhält man

\[\displaystyle -\frac{1}{3}x = -y -\left(-\frac{5}{4}\right)\]

Löst man nun \(x\), indem man beide Seiten der Gleichung durch \(-\frac{1}{3}\) dividiert, erhält man folgendes

\[\displaystyle x=-\frac{1}{-\frac{1}{3}}y+\frac{\frac{5}{4}}{-\frac{1}{3}}\]

und vereinfachen wir endlich die folgenden

\[\displaystyle x=3y-\frac{15}{4}\]

Daher führt die Lösung von \(x\) für die gegebene lineare Gleichung zu \(x = 3y-\frac{15}{4}\).

Wir stellen fest, dass die gegebene Funktion den Horizontalen Linientest besteht, da wir beim Lösen von \(x\) eine Lösung finden und es nur eine Lösung ist.

Die ergebnisse des tests der horizontalen linien

Auf der Grundlage der oben gezeigten Arbeit lässt sich schließen, dass die gegebene Funktion den Horizontal Linientest besteht.

Grafisch lässt sich die Situation wie folgt darstellen:

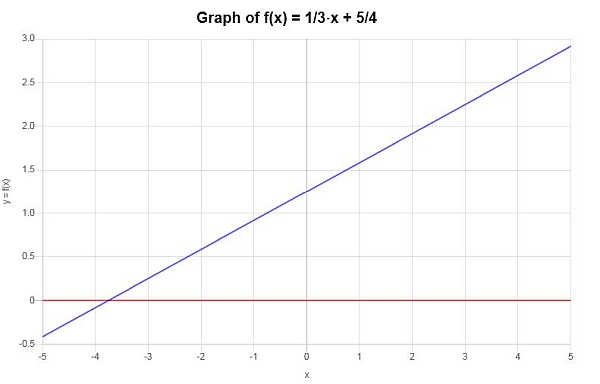
Beispiel: handelt es sich um eine eins-zu-eins-funktion?

Geben Sie mit Hilfe des Horizontaltests an, ob die folgende Funktion eineindeutig ist: \(f(x) = x^3 - 1\)

Lösung: Um festzustellen, ob die gegebene Funktion den Horizontal Linientest besteht oder nicht, müssen wir die Gleichung \(y = x^3 - 1\) für \(x\) lösen und feststellen, ob es keine Lösung, eine Lösung oder mehrere Lösungen gibt.

Erstschritt: In diesem Fall müssen wir zunächst die gegebene Gleichung vereinfachen, und dazu führen wir die folgenden Vereinfachungsschritte durch:

Dann erhalten wir die Lösungen:

\[x_1=\left(y+1\right)^{\frac{1}{3}} \] \[x_2=\frac{1}{2}\left(y+1\right)^{\frac{1}{3}}\left(i\sqrt{3}-1\right) \] \[x_3=-\frac{1}{2}\left(y+1\right)^{\frac{1}{3}}\left(i\sqrt{3}+1\right) \]

Von diesen Lösungen gibt es nur eine echte Lösung, nämlich \(x_1=\left(y+1\right)^{\frac{1}{3}}\). Da wir bei der Lösung von \(x\) eine Lösung finden und es sich um eine einzige reelle Lösung handelt, besteht die gegebene Funktion den Horizontal Linientest.